Common Factors Of 15 And 18

Imagine a vibrant classroom, filled with the eager faces of young mathematicians, their brows furrowed in concentration as they tackle a seemingly simple yet fundamental question. The air buzzes with the quiet scratching of pencils and the occasional murmur of collaborative problem-solving. Today's quest? Unearthing the common threads woven into the numbers 15 and 18.
At its heart, this seemingly elementary exercise in finding the common factors of 15 and 18 illuminates the core principles of number theory, demonstrating how seemingly disparate numbers can share underlying mathematical relationships. Understanding these relationships is crucial for grasping more advanced concepts in mathematics, from simplifying fractions to solving complex algebraic equations. This exploration not only reinforces basic arithmetic skills but also fosters critical thinking and problem-solving abilities, essential tools for navigating the mathematical world and beyond.
The Foundation: What are Factors?
Before diving into the specifics of 15 and 18, let's revisit the definition of a factor. A factor of a number is any integer that divides evenly into that number, leaving no remainder. Think of it as finding the building blocks that, when multiplied together, create the original number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 perfectly. Understanding this basic concept is the key to unlocking the mysteries of common factors.
Unveiling the Factors of 15
Let's begin our exploration with the number 15. What numbers divide evenly into 15? A systematic approach helps ensure we don't miss any.
We start with 1, as 1 is a factor of every number. Then we check 2; it doesn't divide evenly into 15. Next, we try 3: 15 ÷ 3 = 5, so 3 is a factor, and so is 5. Finally, 15 itself is a factor. Therefore, the factors of 15 are 1, 3, 5, and 15.
Discovering the Factors of 18
Now, let's turn our attention to the number 18. Again, we'll use a systematic approach to identify its factors.
We begin with 1, which, as always, is a factor. Two divides evenly into 18 (18 ÷ 2 = 9), so 2 and 9 are factors. Three also divides evenly (18 ÷ 3 = 6), making 3 and 6 factors. Four and five don't work, but 18 itself is a factor. Thus, the factors of 18 are 1, 2, 3, 6, 9, and 18.
The Intersection: Identifying Common Factors
The next step is to compare the list of factors for 15 and 18. We're looking for the numbers that appear in both lists – the shared building blocks of these two numbers.
The factors of 15 are: 1, 3, 5, and 15. The factors of 18 are: 1, 2, 3, 6, 9, and 18. By comparing these lists, we can identify the common factors.
The common factors of 15 and 18 are 1 and 3. These are the numbers that divide evenly into both 15 and 18.
The Greatest Common Factor (GCF)
Among the common factors, there's often one that stands out: the greatest common factor, or GCF. This is the largest number that divides evenly into both numbers.
In the case of 15 and 18, the common factors are 1 and 3. Clearly, 3 is larger than 1. Therefore, the greatest common factor of 15 and 18 is 3.
Why Does This Matter? The Significance of Common Factors
Understanding common factors isn't just an abstract mathematical exercise; it has practical applications in various areas of mathematics and beyond. One of the most common uses is in simplifying fractions.
For example, consider the fraction 15/18. By dividing both the numerator (15) and the denominator (18) by their greatest common factor (3), we can simplify the fraction to 5/6. This simplified fraction is equivalent to the original but is expressed in its simplest form.
Furthermore, the concept of common factors plays a crucial role in algebra. When factoring expressions, identifying common factors is often the first step in simplifying and solving equations. It's also essential in more advanced areas like cryptography and computer science.
Beyond the Classroom: Real-World Applications
The principles learned in finding common factors extend beyond the confines of the classroom and into real-world scenarios. Think about dividing items equally among groups.
For instance, if you have 15 apples and 18 oranges and want to create identical fruit baskets, the greatest common factor (3) tells you that you can make 3 baskets, each containing 5 apples and 6 oranges. This ensures fairness and equal distribution.
Construction, design, and even music rely on mathematical principles, including the concept of factors and multiples. From dividing spaces into equal sections to creating harmonious musical intervals, the understanding of these foundational concepts is invaluable.
Cultivating Mathematical Thinking
The journey to understanding common factors is not just about memorizing definitions and procedures. It's about developing a way of thinking – a mathematical mindset that embraces logic, problem-solving, and critical analysis.
By encouraging students to explore, experiment, and question, we foster a deeper understanding of mathematical concepts. This goes beyond rote learning and empowers them to apply their knowledge in new and creative ways. The process of discovering common factors, though seemingly simple, is a stepping stone to cultivating this mathematical thinking.
A Final Thought: The Beauty of Numbers
The exploration of common factors of 15 and 18 may seem like a small step in the vast world of mathematics, but it reveals a fundamental truth: numbers are interconnected in beautiful and meaningful ways. These connections, once understood, unlock a deeper appreciation for the elegance and power of mathematics.
By uncovering these relationships, we not only improve our mathematical skills but also develop a greater sense of curiosity and wonder about the world around us. So, the next time you encounter a seemingly simple mathematical problem, remember that it may hold the key to a much larger understanding.
And who knows? Maybe the next great mathematical breakthrough will start with the simple question: What are the common factors of 15 and 18?












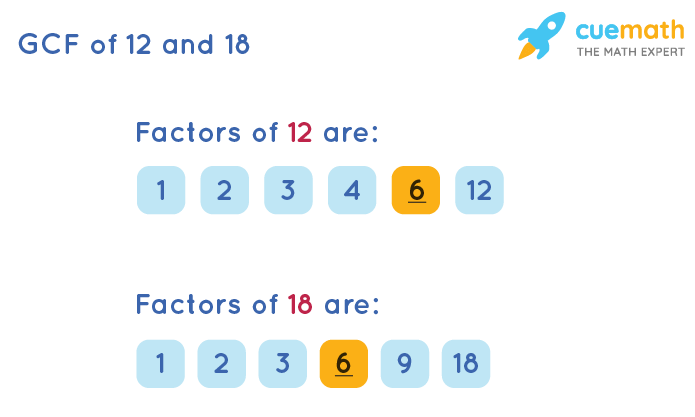



.PNG)

