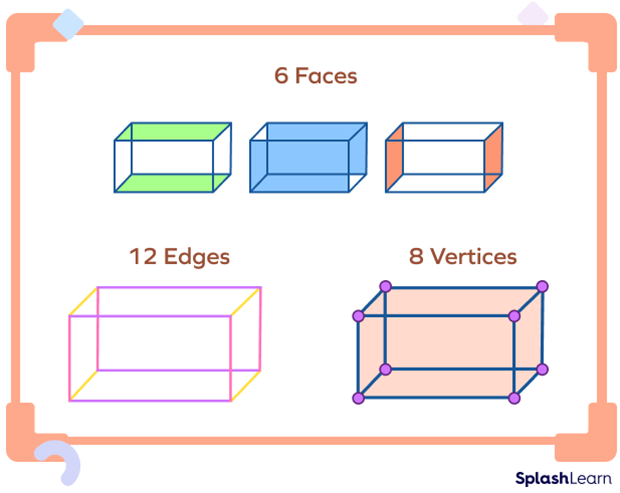
How Many Edges Of A Cuboid Meet In A Vertex
The question of how many edges of a cuboid meet at a single vertex might seem simple, yet it underscores fundamental principles of geometry and spatial reasoning. This seemingly basic inquiry serves as a gateway to understanding more complex three-dimensional structures and their properties. Understanding this concept is crucial for various fields, from architecture and engineering to computer graphics and design.
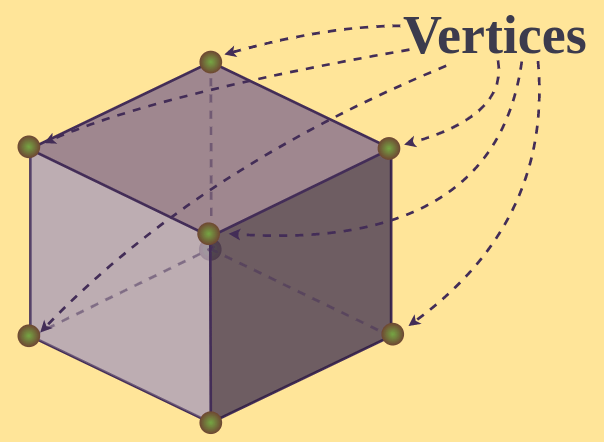
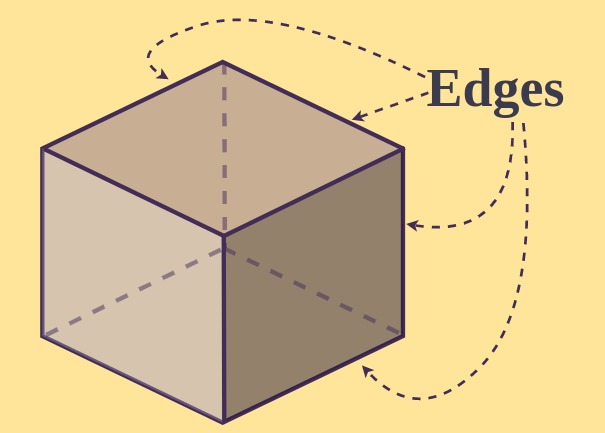
At any given vertex of a standard cuboid, precisely three edges converge. This fact is a direct consequence of the cuboid's inherent structure as a rectangular prism. Let's delve into the details of this geometric feature and its implications.
Defining a Cuboid
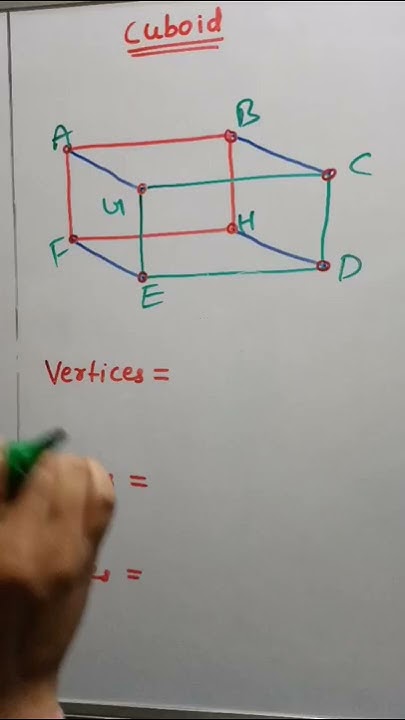
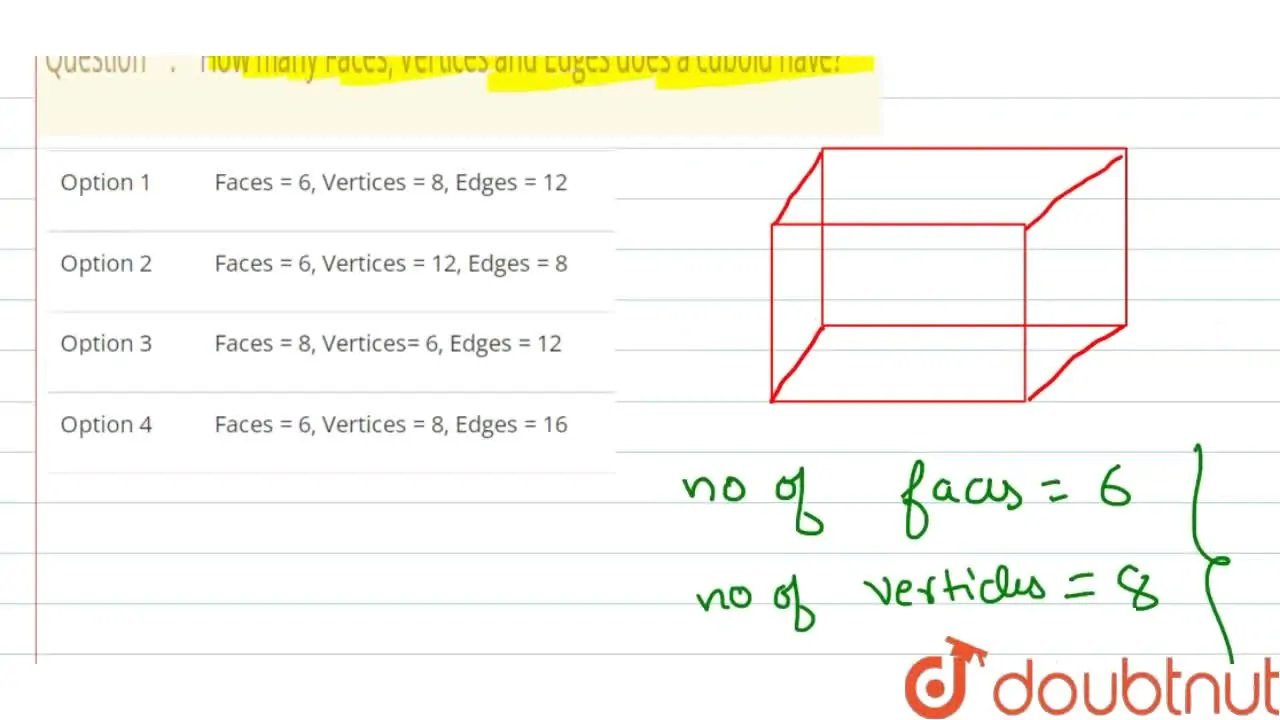
A cuboid, also known as a rectangular prism, is a three-dimensional solid object bounded by six faces, which are rectangles. These faces meet at right angles, defining the shape's characteristic rectangular corners. Key features include its length, width, and height, each representing a dimension along which the cuboid extends.
The Significance of Edges and Vertices
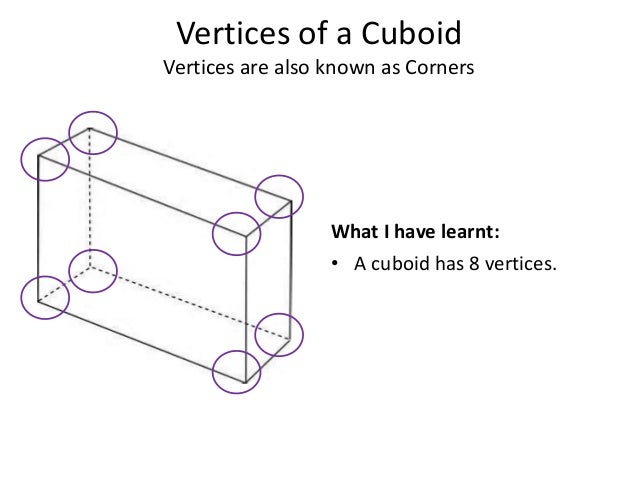
In geometry, an edge is a line segment where two faces meet, while a vertex is a point where edges intersect. In a cuboid, the edges define the skeletal structure, and the vertices are the points where these edges come together. The specific configuration of edges meeting at a vertex dictates the local geometry of the shape.
Why Three Edges?
Consider a corner of any common rectangular object, such as a box or a brick. At that corner, you'll notice that three edges are required to define the three-dimensional space. These edges represent the intersection of three faces, each orthogonal (at a right angle) to the others.
This is not a coincidence but a fundamental property of rectangular geometry. A deviation from three edges would either result in a different type of solid or a warped, non-rectangular form.
Implications and Applications
Understanding that three edges meet at a vertex has broad implications. In architecture, this knowledge is fundamental to designing stable and structurally sound buildings. Engineers rely on this principle when constructing frameworks and ensuring load-bearing capabilities.
In computer graphics, this principle is vital for rendering realistic 3D models. Accurately representing the geometry of objects, including the correct number of edges at each vertex, is crucial for visual fidelity.
"The precise intersection of edges at a vertex defines the object's visual integrity," Dr. Anya Sharma, a professor of computational geometry, explained.
Beyond the Cuboid
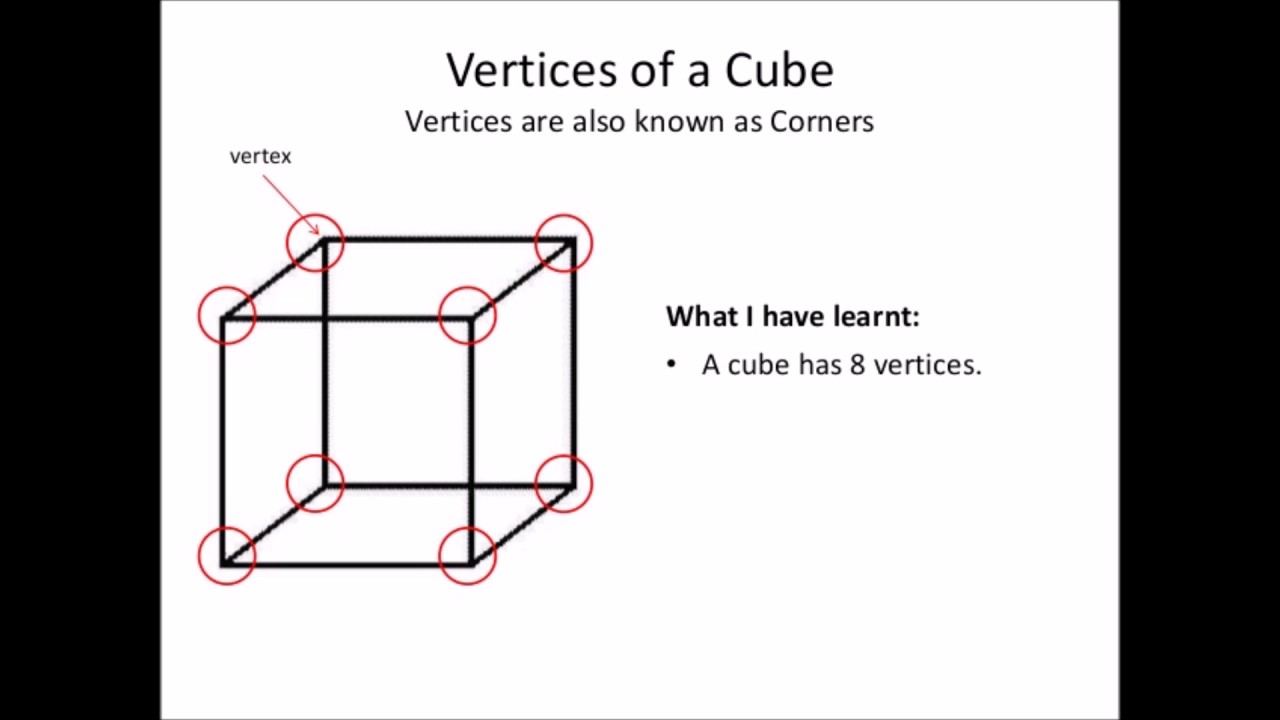
While a cuboid offers a clear example, this concept extends to other polyhedra. The number of edges meeting at a vertex can vary depending on the shape. For instance, a tetrahedron has three edges meeting at each vertex, while a cube has the same number as a cuboid.
Understanding these variations is essential for analyzing and classifying different geometric solids. Each configuration dictates specific properties of the shape.
Conclusion
The seemingly simple question of how many edges of a cuboid meet at a vertex highlights fundamental principles of geometry. The answer, three, reflects the core structure of rectangular prisms. This knowledge is important not only for theoretical mathematics but also for practical applications in various fields, solidifying its importance in both understanding and shaping the world around us.


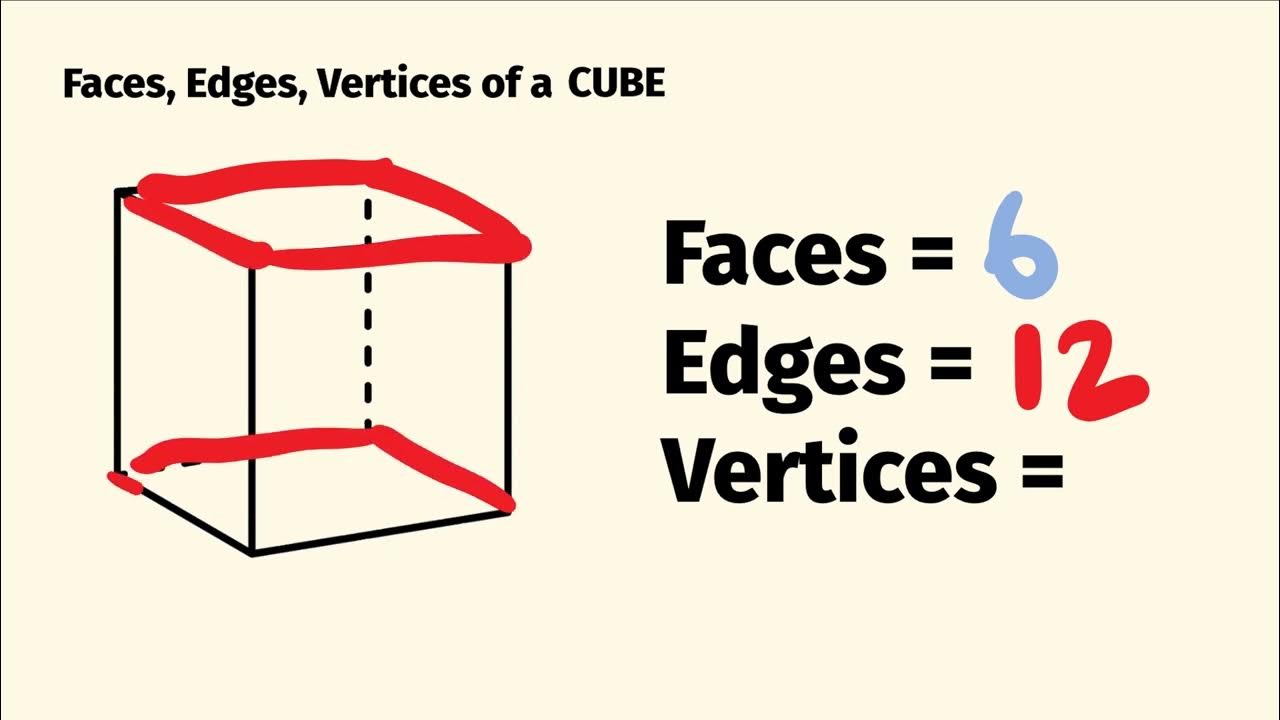




![How Many Edges Of A Cuboid Meet In A Vertex How many faces edges and vertices does a cube have[solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/cube-1614171313.png)