How Many Eighths In A Quarter

Imagine a cozy kitchen, sunlight streaming through the window, illuminating a small, well-worn scale. A baker, perhaps a grandparent teaching a grandchild, carefully measures ingredients for a cherished family recipe. The air is filled with the sweet scent of vanilla and cinnamon, and the quiet murmur of fractions fills the space: halves, quarters, and, inevitably, eighths.

At its core, the question of how many eighths are in a quarter boils down to understanding basic fractions. This seemingly simple calculation holds significance in various everyday contexts, from cooking and baking to financial transactions and understanding measurements in numerous fields.

Fractions, the building blocks of numerical understanding, represent parts of a whole. Mastering them allows us to accurately divide and share quantities, making precise calculations possible in many scenarios.

The Basics of Fractions

A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator represents the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering.

For instance, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts, and the numerator (1) indicates we have one of those parts.

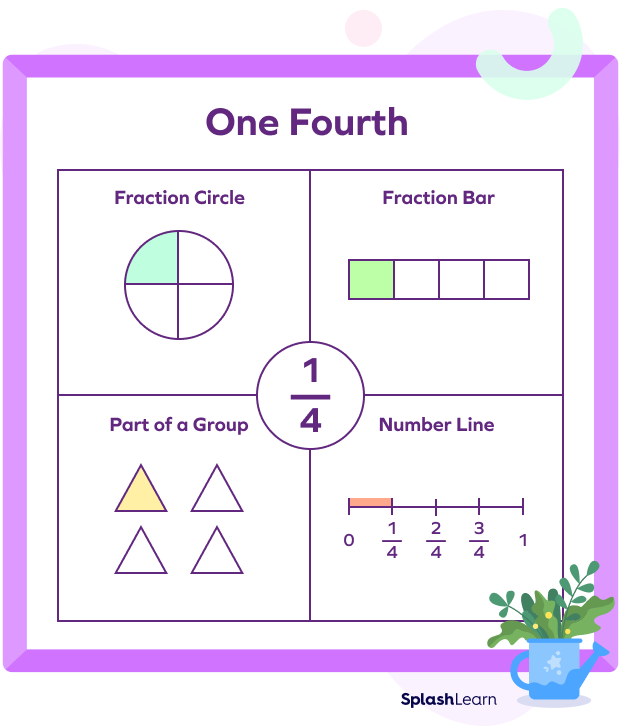
Similarly, 1/4 means the whole is divided into four equal parts, and we're looking at one of those parts. And 1/8 means the whole is divided into eight equal parts, and we're focusing on one of them.

Calculating Eighths in a Quarter

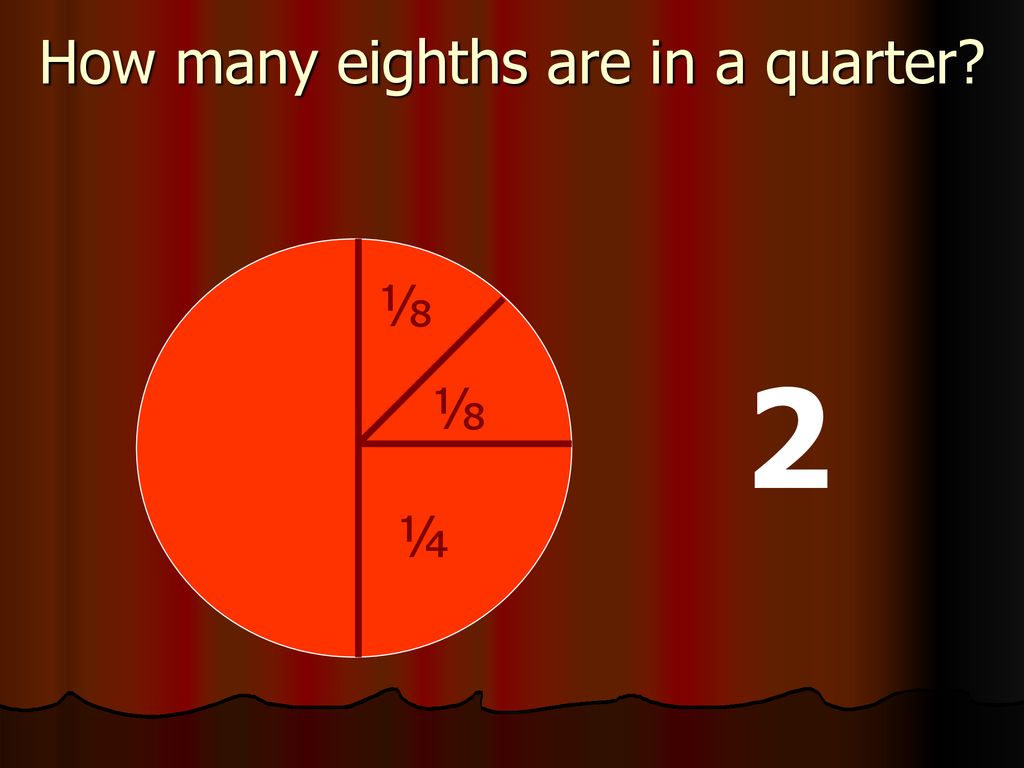
The question is, how many 1/8 pieces are needed to make up 1/4? To solve this, we need to find a common denominator. Both fractions should represent portions of the same whole divided into the same number of parts.

We can easily convert 1/4 into an equivalent fraction with a denominator of 8. Since 8 is twice as big as 4, we multiply both the numerator and denominator of 1/4 by 2.

This gives us (1 x 2) / (4 x 2) = 2/8. Therefore, 1/4 is equal to 2/8.

This means that there are two eighths (2/8) in one quarter (1/4). Visualize a pie cut into four slices; each slice is a quarter. Now imagine cutting each of those slices in half. You'd then have eight slices, each an eighth, and each original quarter slice would now be made up of two eighths.

Real-World Applications

Understanding this relationship between fractions is more than just a mathematical exercise. It has practical implications across various fields.

Cooking and Baking

Recipes often use fractional measurements like 1/4 cup or 1/8 teaspoon. Knowing how these fractions relate helps in scaling recipes up or down.

For example, if a recipe calls for 1/4 cup of sugar and you want to double the recipe, you would need 1/2 cup of sugar, which is equivalent to four eighths of a cup.

Construction and Engineering

Measurements in construction and engineering frequently involve fractions of an inch or other units. Accuracy is paramount in these fields, so knowing how to convert between fractions is vital.

Imagine needing to cut a piece of wood to a specific length. Knowing the relationship between quarters and eighths of an inch ensures precision and prevents costly errors.

Financial Transactions

Although less common in everyday currency, fractions can still appear in financial contexts, such as stock prices, where changes are often reported in fractions of a dollar. Understanding fractions helps interpret these changes accurately.

For example, a stock might increase by 1/4 of a dollar, which is the same as an increase of 2/8 of a dollar.

Education

From elementary school onwards, fractions are a fundamental part of math education. Grasping the relationship between different fractions is crucial for more advanced mathematical concepts.

Teachers use various tools and techniques to help students visualize and understand fractions, reinforcing the idea that fractions are simply parts of a whole.

The Psychology of Fractions

Beyond the practical applications, there's also a psychological aspect to understanding fractions. Mastering fractions can boost confidence in one's mathematical abilities, making more complex problems seem less daunting. It's about feeling empowered by numbers rather than intimidated by them.

When individuals develop a solid understanding of fractions, they become more comfortable with quantitative reasoning in general, which can benefit them in numerous areas of life.

Successfully navigating calculations involving fractions contributes to a general sense of competence and problem-solving ability.

Visual Aids and Tools

Numerous visual aids and tools can help demystify fractions. Pie charts, fraction bars, and online calculators all provide different ways to conceptualize and manipulate fractions.

Teachers often use these aids in classrooms to make the learning process more engaging and intuitive. These visual representations cater to different learning styles and preferences.

Whether it's a physical manipulative or a digital simulation, the goal is to make the abstract concept of fractions more concrete and relatable.

The Importance of Conceptual Understanding

While memorizing rules and formulas can be helpful, developing a conceptual understanding of fractions is essential for long-term retention and application. This means understanding why the rules work, not just how to apply them.

For example, rather than simply memorizing the rule for adding fractions, understanding why a common denominator is necessary allows you to apply the concept to more complex problems.

True understanding empowers individuals to solve problems creatively and adapt to new situations, rather than relying solely on rote memorization.

Fractions in Historical Context

The use of fractions dates back to ancient civilizations. Egyptians and Babylonians developed sophisticated systems for working with fractions to solve problems related to agriculture, construction, and trade. Their ingenuity laid the groundwork for the mathematics we use today.

Over time, different cultures refined and expanded upon these early systems, leading to the modern notation and methods we use today. The history of fractions is a testament to human ingenuity and the enduring quest to understand the world through numbers.

From ancient surveying techniques to modern financial modeling, fractions have played a crucial role in advancing human knowledge and progress.

The Beauty of Simplicity

So, how many eighths are in a quarter? The answer, two, is a testament to the elegant simplicity of mathematics. It's a reminder that even complex concepts can be broken down into smaller, more manageable parts.

This principle applies not only to mathematics but also to many aspects of life. By breaking down complex tasks into smaller steps, we can make them less overwhelming and more achievable. Embrace the power of fractions, and let them guide you towards a deeper understanding of the world around you. And remember that the humble eighth, like all fractions, plays a vital role in the grand tapestry of numbers.

That simple calculation, so fundamental yet so powerful, connects us to the baker in the sunlit kitchen, the engineer designing a bridge, and the student mastering a new concept. It's a small piece of a larger puzzle, and mastering it empowers us all.