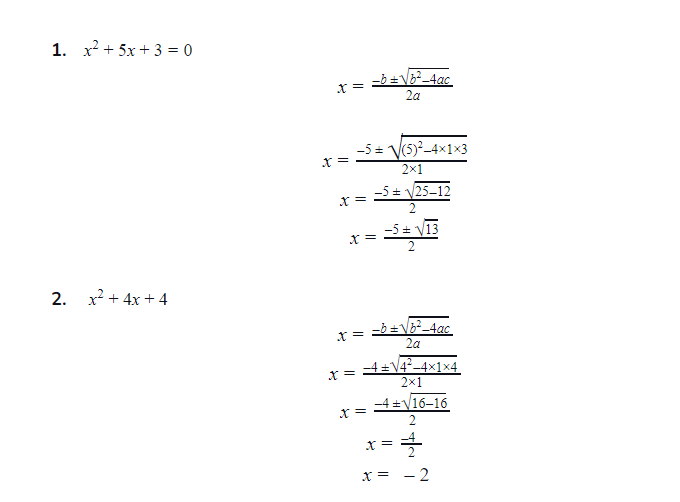How To Find The Positive Solution Of An Equation

Navigating the world of mathematics often requires finding specific solutions to equations. Among these, positive solutions hold particular significance in various real-world applications, from physics and engineering to economics and finance.
The process of finding a positive solution depends heavily on the type of equation being addressed. Linear, quadratic, or more complex equations each demand distinct strategies.
Understanding the Equation Type
The first step is always identifying the type of equation at hand. This identification dictates the applicable methods for solution.
Linear equations, characterized by a highest power of one for the variable, are relatively straightforward to solve.
Quadratic equations, containing a variable raised to the power of two, require techniques like factoring, completing the square, or using the quadratic formula.
Solving Linear Equations
To find the positive solution of a linear equation, isolate the variable on one side of the equation. This involves performing the same operations on both sides until the variable stands alone.
For example, consider the equation 2x + 3 = 7. Subtracting 3 from both sides yields 2x = 4, and then dividing both sides by 2 gives x = 2.
Since 2 is a positive number, it is the positive solution we sought.
Tackling Quadratic Equations
Quadratic equations, represented in the general form ax2 + bx + c = 0, offer multiple solution paths.
Factoring involves rewriting the equation as a product of two binomials. However, it's not always easy to apply it for all equation types.
The quadratic formula, x = (-b ± √(b2 - 4ac)) / 2a, guarantees a solution, regardless of factorability. After applying the formula, check for positive solutions.
Completing the square is another method to re-write the equation as a squared term. It is useful in derivations and for deeper theoretical understanding.
Beyond the Basics
For more complex equations, numerical methods often become necessary. Newton-Raphson method is an iterative approach that uses derivatives to approximate the roots of a function.
Graphical methods, such as plotting the equation and visually identifying the points where the graph intersects the x-axis with a positive x-value, can also be helpful. These techniques are especially helpful when no other analytical solutions can be found.
Sophisticated mathematical software packages like MATLAB or Mathematica offer powerful tools for solving complex equations and finding their roots.
Verifying the Solution
Crucially, after obtaining a potential positive solution, it must be verified by substituting it back into the original equation.
This step ensures that the calculated value indeed satisfies the equation.
Moreover, consider the context of the problem. Sometimes, even if a solution is mathematically positive, it might not be physically or logically meaningful.
The Importance of Positive Solutions
Positive solutions are encountered everywhere in applied mathematics.
For instance, in physics, quantities like mass, length, and time are almost always expressed as positive values.
In finance, concepts such as interest rates and profit margins are usually positive.
Finding and understanding the positive solution provides not only a mathematically correct answer, but also one with significant meaning to your particular application.