Is 33 A Prime Number Or A Composite Number
The question, seemingly simple, has ignited a surprising debate across online forums and academic circles: is 33 a prime number or a composite number? This inquiry, often relegated to elementary mathematics, touches upon the foundational principles of number theory and has sparked passionate discussions about mathematical literacy.
At its core, this debate highlights a potential gap in understanding basic number concepts. It reveals a need for reinforcing fundamental mathematical principles within the broader population.
The Core Question: Prime or Composite?
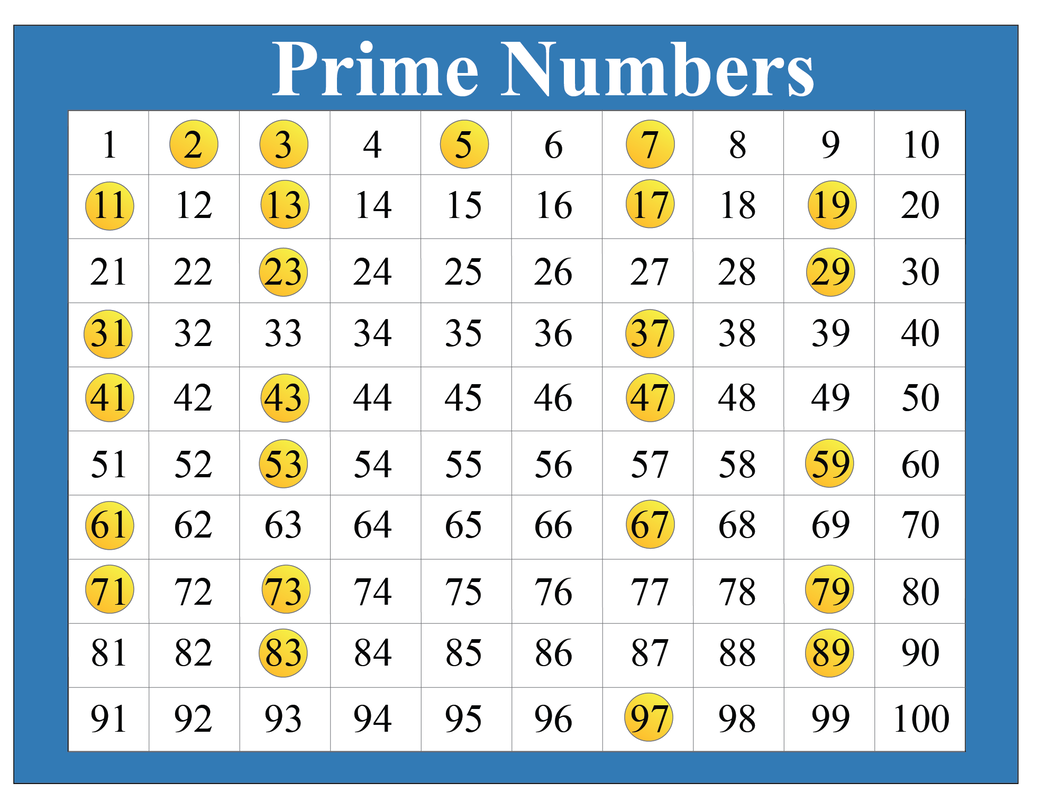
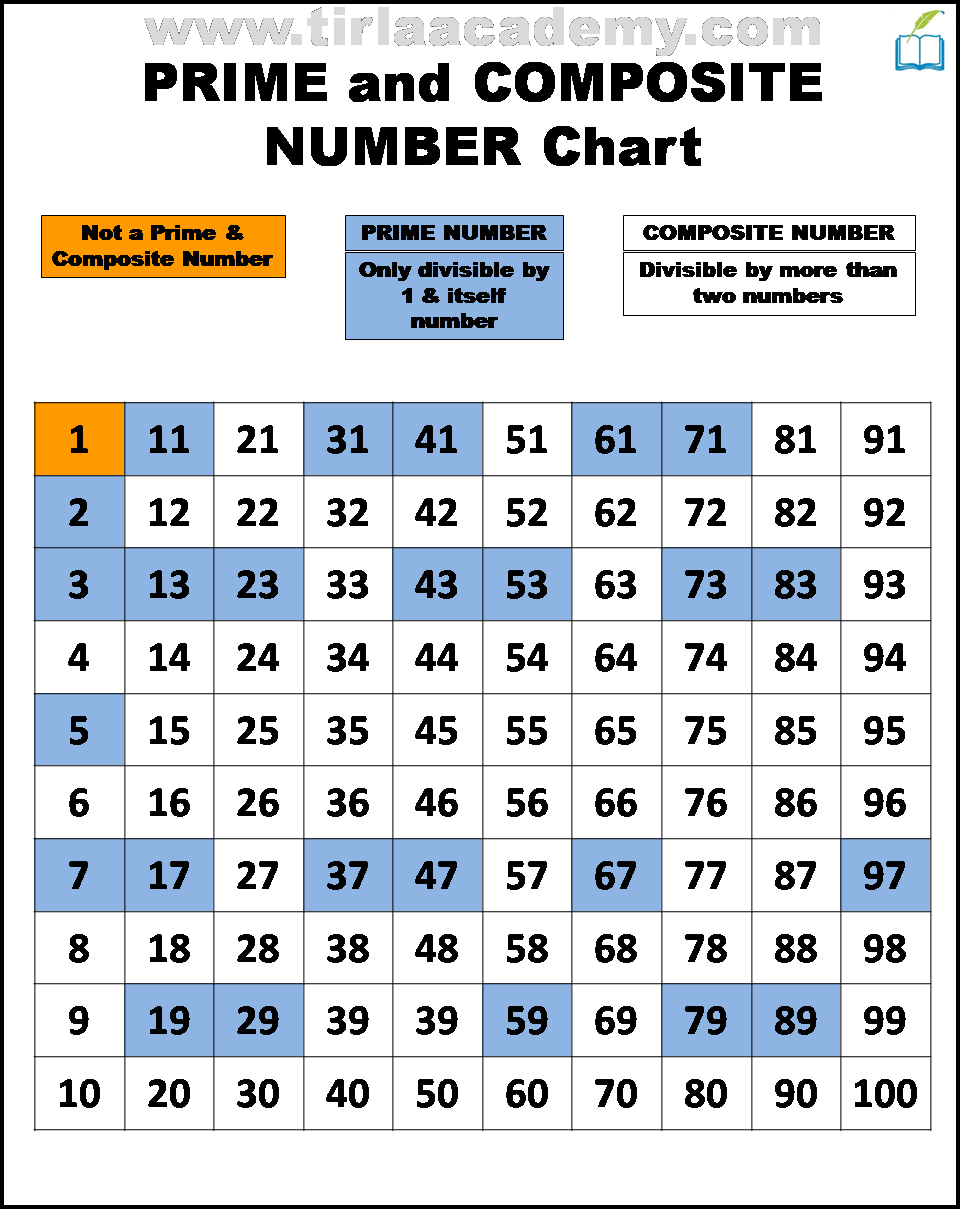
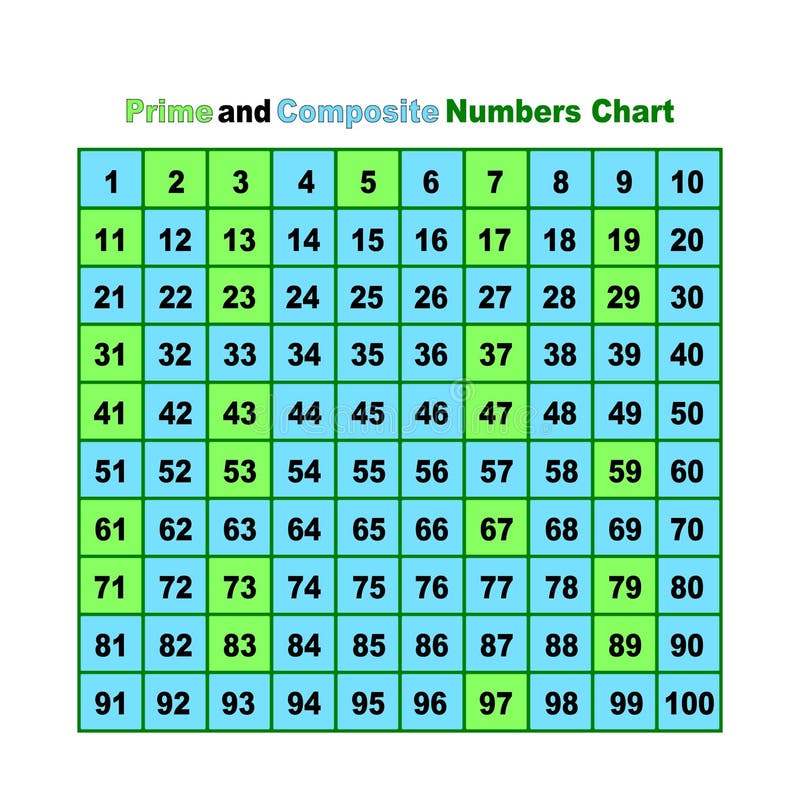
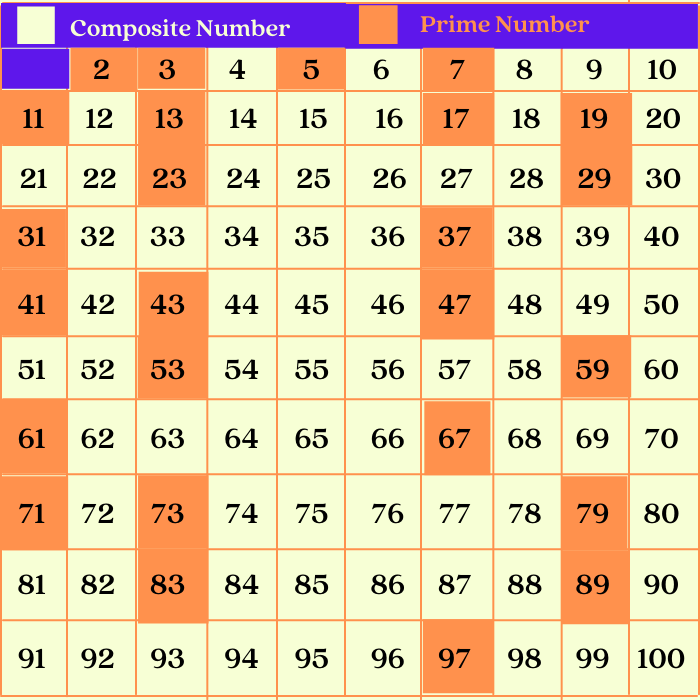
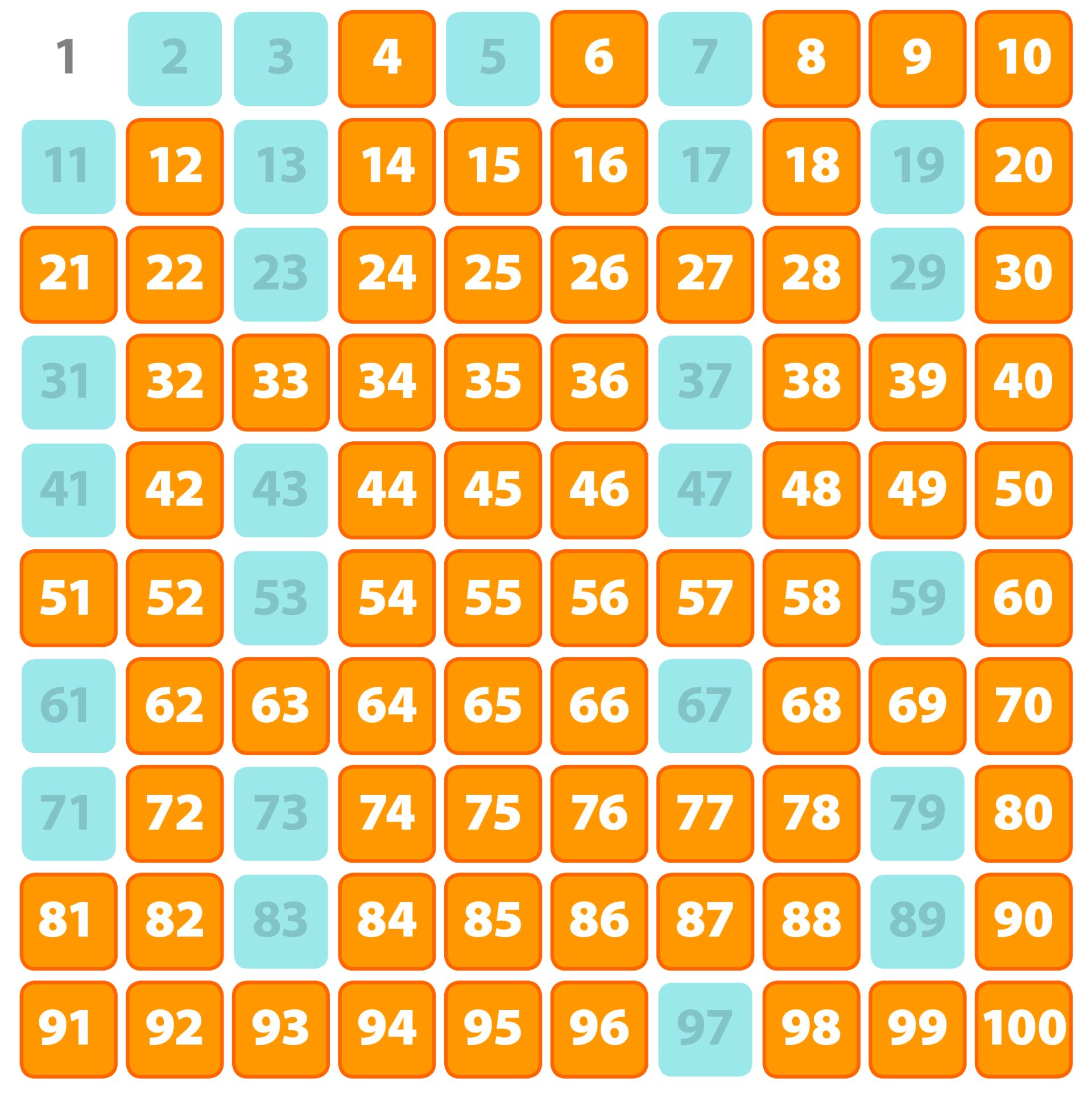
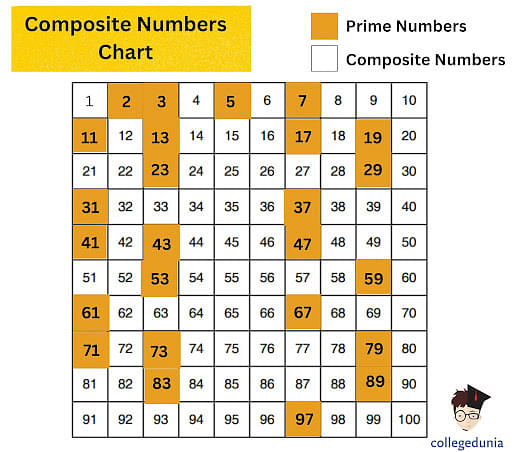
The debate centers on the definitions of prime and composite numbers. A prime number, by definition, is a whole number greater than 1 that has only two divisors: 1 and itself. Composite numbers, on the other hand, are whole numbers greater than 1 that have more than two divisors.
Numbers like 2, 3, 5, 7, and 11 fit the definition of prime, having only two factors. While numbers like 4, 6, 8, 9, and 10 are classified as composite due to their multiple factors.
The argument surrounding 33 hinges on whether it fits either of these categories. Let's delve deeper into the mathematical properties of 33 to determine its classification.
Divisibility of 33: A Mathematical Exploration
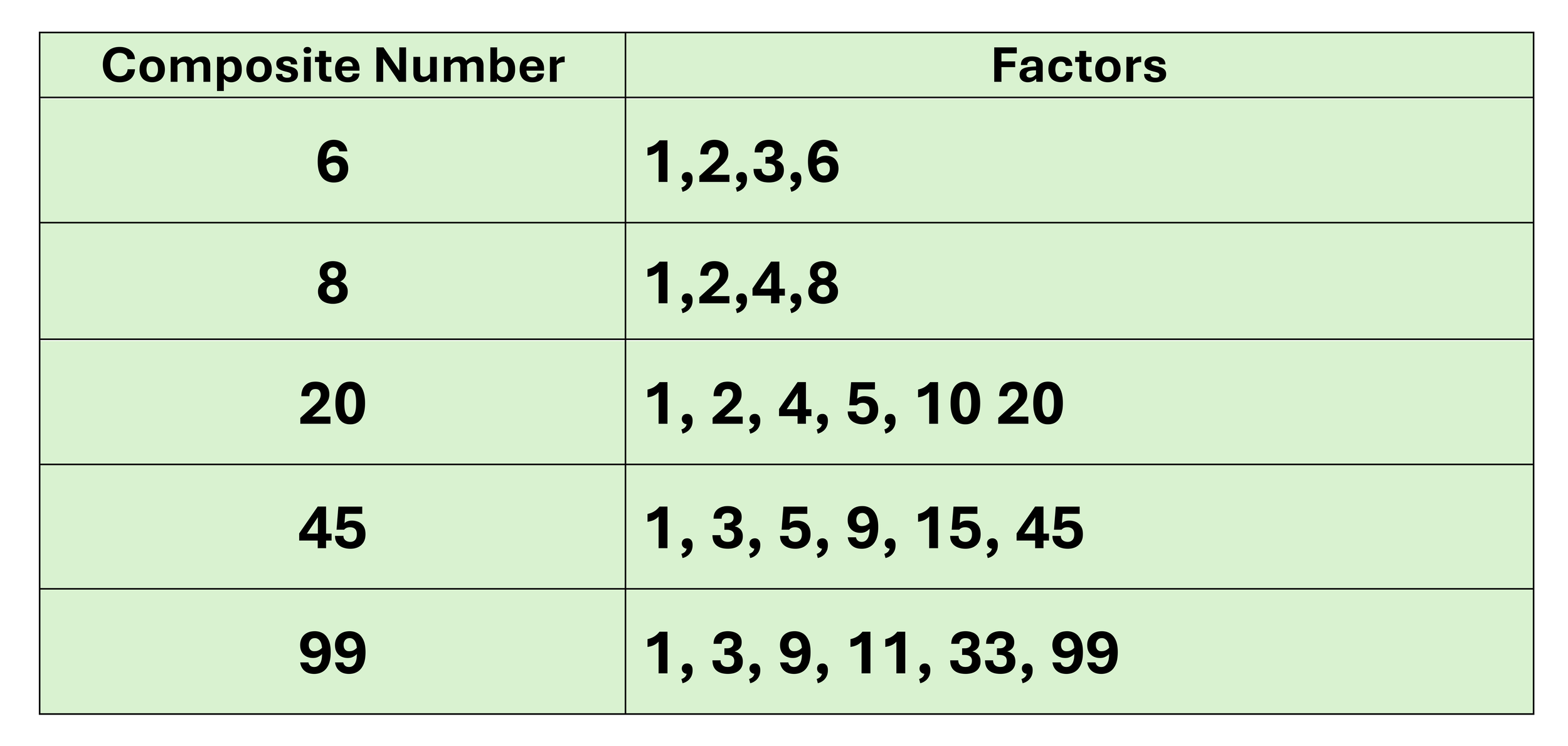
To determine if 33 is prime or composite, we must identify its divisors. A divisor is a number that divides evenly into another number, leaving no remainder.
The divisors of 33 are 1, 3, 11, and 33. This is because 33 ÷ 1 = 33, 33 ÷ 3 = 11, 33 ÷ 11 = 3, and 33 ÷ 33 = 1.
Since 33 has more than two divisors (1 and itself), it cannot be a prime number. Therefore, 33 is definitively a composite number.
The Importance of Foundational Mathematical Knowledge
The discussions surrounding this simple question shed light on the importance of foundational mathematical knowledge. Many argue that a solid understanding of basic number theory is crucial for everyday life.
"A firm grasp of prime and composite numbers is not just for mathematicians," stated Dr. Emily Carter, a mathematics professor at the University of California, Berkeley. "It's a fundamental skill that supports logical reasoning and problem-solving abilities in various fields."
The ability to quickly identify prime and composite numbers can be beneficial in areas like cryptography, computer science, and even basic financial planning.
Misconceptions and Common Errors
One common misconception is confusing prime numbers with odd numbers. While all prime numbers (except for 2) are odd, not all odd numbers are prime.
The number 9, for example, is odd but it is composite, as it is divisible by 1, 3, and 9. This confusion can lead to errors in identifying prime and composite numbers.
Another error stems from overlooking the divisibility rules. For instance, knowing that a number is divisible by 3 if the sum of its digits is divisible by 3 would quickly reveal that 33 (3 + 3 = 6) is divisible by 3.
Educational Implications and Outreach Efforts
The widespread discussion about the primality of 33 has spurred educational initiatives aimed at reinforcing basic mathematical concepts. Many online resources and educational platforms are now focusing on improving understanding of number theory.
Organizations like the National Council of Teachers of Mathematics (NCTM) are developing resources and professional development programs to help educators teach number theory more effectively.
These efforts aim to ensure that students have a solid foundation in mathematics, reducing the likelihood of similar misconceptions in the future. NCTM emphasizes the importance of hands-on activities and real-world applications to make learning more engaging and relevant.
The Broader Impact: Mathematical Literacy in Society
The incident highlights a broader concern about mathematical literacy in society. A lack of understanding of basic mathematical concepts can have significant implications for individuals and society as a whole.
From managing personal finances to understanding scientific data, mathematical skills are essential for navigating the modern world. Improving mathematical literacy can empower individuals to make informed decisions and participate more fully in society.
Professor David Black from Stanford University comments, "Mathematical literacy is not just about knowing formulas; it's about developing critical thinking and problem-solving skills that are applicable in all aspects of life."
Moving Forward: A Focus on Mathematical Foundations
The debate surrounding 33 serves as a valuable reminder of the importance of strengthening mathematical foundations. By emphasizing fundamental concepts and addressing common misconceptions, we can foster greater mathematical literacy and empower individuals to succeed in a world increasingly reliant on quantitative reasoning.
Educational institutions, parents, and individuals must prioritize building a strong base in mathematical principles. Continued efforts to improve mathematics education are crucial for fostering a more informed and empowered society.
Ultimately, the question of whether 33 is prime or composite is not just a trivial matter; it's an opportunity to promote a deeper appreciation for mathematics and its vital role in our lives. The answer, unequivocally, is that 33 is a composite number, divisible by 1, 3, 11, and itself.