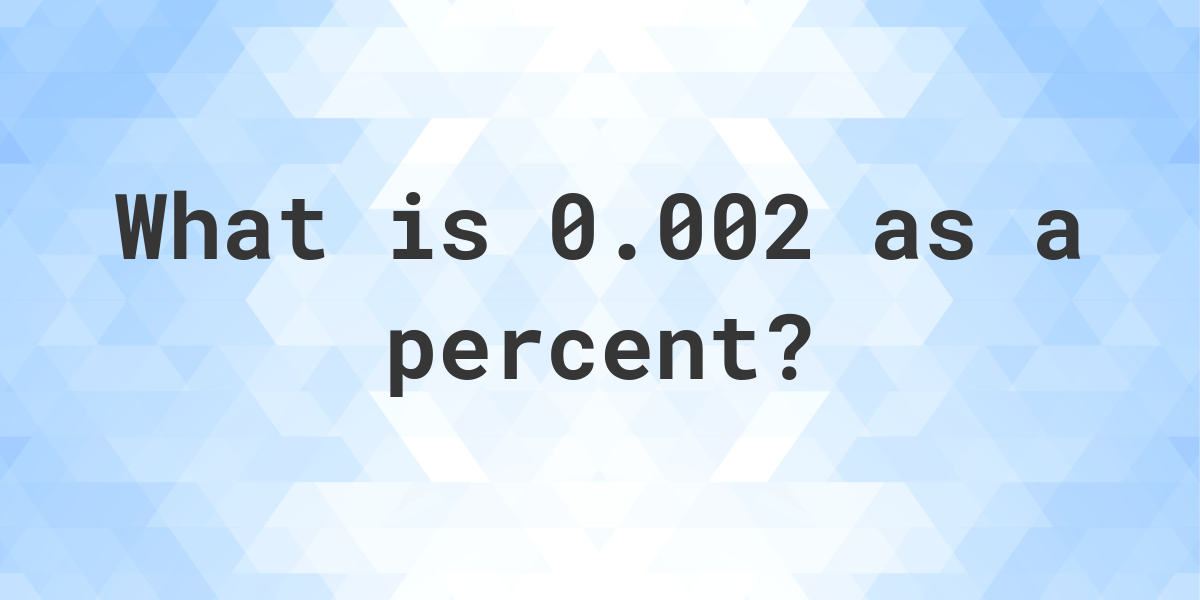What Is 0.002 As A Percent

In an era dominated by data-driven decision-making, even the smallest numerical values can hold significant implications. Understanding how to interpret and convert these values into relatable formats, like percentages, is crucial for informed analysis and communication. The seemingly simple question of "what is 0.002 as a percent?" belies a deeper need for numeracy and the ability to accurately translate quantitative information.
This article will explore the conversion of the decimal 0.002 into a percentage. This fundamental skill is applicable across various fields, from finance and economics to science and everyday life. We will delve into the methodology behind the conversion, illustrate its practical uses, and address common misconceptions surrounding percentage calculations.
The Core Calculation
Converting a decimal to a percentage involves a straightforward mathematical operation. The basic principle is to multiply the decimal by 100. This shifts the decimal point two places to the right, effectively expressing the value as a fraction of one hundred.
Therefore, to convert 0.002 to a percentage, we perform the following calculation: 0.002 * 100 = 0.2%. This means that 0.002 is equivalent to two-tenths of one percent.
Practical Applications
Understanding how to convert small decimals into percentages is essential in various real-world scenarios. One common application is in financial contexts, such as calculating interest rates or investment returns. A 0.002 interest rate on a savings account, for example, translates to a 0.2% annual yield.
In scientific research, this conversion can be used to express concentrations or probabilities. For instance, a solution containing 0.002 of a specific substance might be described as having a 0.2% concentration. This offers a more intuitive understanding compared to the decimal form.
Another practical application lies in quality control and manufacturing. If a product has a defect rate of 0.002, it means that 0.2% of the products are faulty. This information is vital for process improvement and maintaining quality standards.
Common Misconceptions
A frequent misconception is the belief that multiplying by 100 automatically results in a large percentage. When dealing with decimals smaller than 0.01, the resulting percentage will also be a relatively small number, less than 1%. It's crucial to maintain accuracy and avoid rounding errors that could distort the actual value.
Another misunderstanding is the difference between percentage points and percentages. A percentage point is an arithmetic difference between two percentages. Confusing these terms can lead to misinterpretations, particularly when analyzing changes in statistical data.
It's also important to remember that percentages are always relative to a whole, which is typically 100. Failure to define the whole can render the percentage meaningless. The context in which the percentage is used is crucial for proper interpretation.
Perspectives and Considerations
From a statistical perspective, understanding small percentages can be vital for hypothesis testing and significance analysis. P-values, often expressed as decimals, are frequently converted to percentages to assess the likelihood of an observed result occurring by chance.
In the business world, even seemingly insignificant percentages can translate into substantial financial gains or losses when applied to large volumes. A 0.2% improvement in efficiency, for example, can result in considerable cost savings for a large-scale operation.
From an educational standpoint, mastering the conversion between decimals and percentages is a foundational skill in mathematics. It reinforces the understanding of place value and the relationship between different numerical representations.
The Importance of Accuracy
In fields like financial analysis and scientific research, accuracy is paramount. Even small errors in percentage calculations can have significant consequences, leading to incorrect conclusions or flawed decision-making. This underscores the need for careful attention to detail and the use of appropriate tools for calculation.
Tools such as calculators and spreadsheet software can help minimize the risk of human error. However, it's equally important to understand the underlying principles of percentage calculations to verify the accuracy of the results obtained.
Regular practice and reinforcement of these mathematical concepts are essential for maintaining proficiency and confidence in handling quantitative data.
Looking Ahead
As the volume of data continues to grow exponentially, the ability to interpret and communicate numerical information effectively will become even more crucial. The skill of converting decimals to percentages, while seemingly basic, represents a fundamental building block for data literacy.
Future educational curricula should emphasize the practical applications of percentage calculations across various disciplines. This will equip individuals with the necessary skills to navigate an increasingly data-driven world.
Ultimately, a strong foundation in numeracy, including a thorough understanding of percentages, empowers individuals to make informed decisions and contribute meaningfully to society. This is a skill critical for everyone.