What Is A Benchmark In Fractions
Fractions, often a source of frustration for students and adults alike, can be made more approachable through the strategic use of benchmark fractions. These common, easily visualized fractions act as reference points, simplifying comparisons and estimations. Understanding benchmark fractions is a fundamental skill in mathematics education, impacting everything from basic arithmetic to more complex problem-solving.
So, what exactly are benchmark fractions, and why are they so important? This article will delve into the definition, significance, and practical applications of these essential mathematical tools.
Understanding the Basics
At their core, benchmark fractions are familiar fractions that serve as mental reference points when working with other fractions. These commonly used fractions are easy to visualize and understand, helping individuals quickly estimate and compare the values of other fractions.
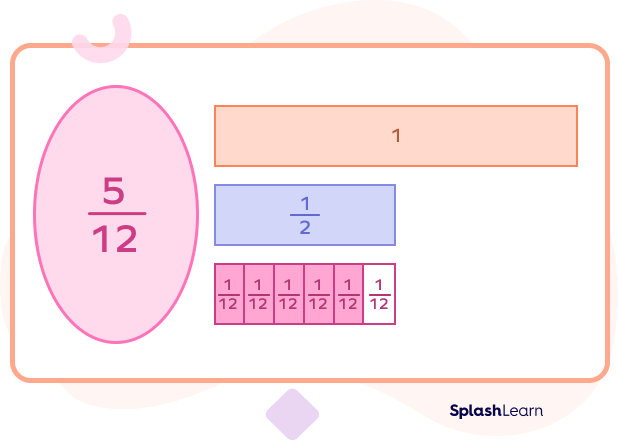
Examples of benchmark fractions include 1/4, 1/3, 1/2, 2/3, and 3/4. These fractions are often represented visually using fraction bars or pie charts, making them readily accessible to learners of all ages.
The Significance of Benchmarks
The importance of benchmark fractions lies in their ability to provide a framework for understanding the relative size of other fractions. Instead of struggling to precisely calculate the value of a less common fraction, one can compare it to a nearby benchmark fraction.
This process allows for quick estimations and simplifies complex calculations. According to the National Council of Teachers of Mathematics (NCTM), a strong understanding of benchmark fractions is crucial for developing number sense and proportional reasoning.
Estimating and Comparing Fractions
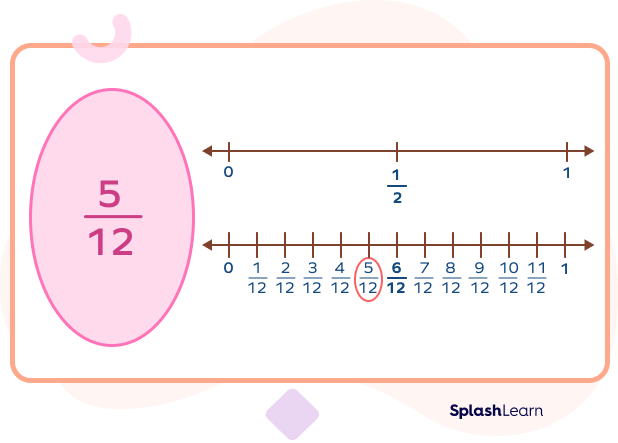
One of the primary uses of benchmark fractions is in estimating the value of other fractions. For instance, if you encounter the fraction 5/8, you can quickly recognize that it is slightly more than 1/2.
This comparison provides a reasonable estimate without the need for precise calculation. Benchmark fractions are also incredibly useful when comparing two or more fractions.
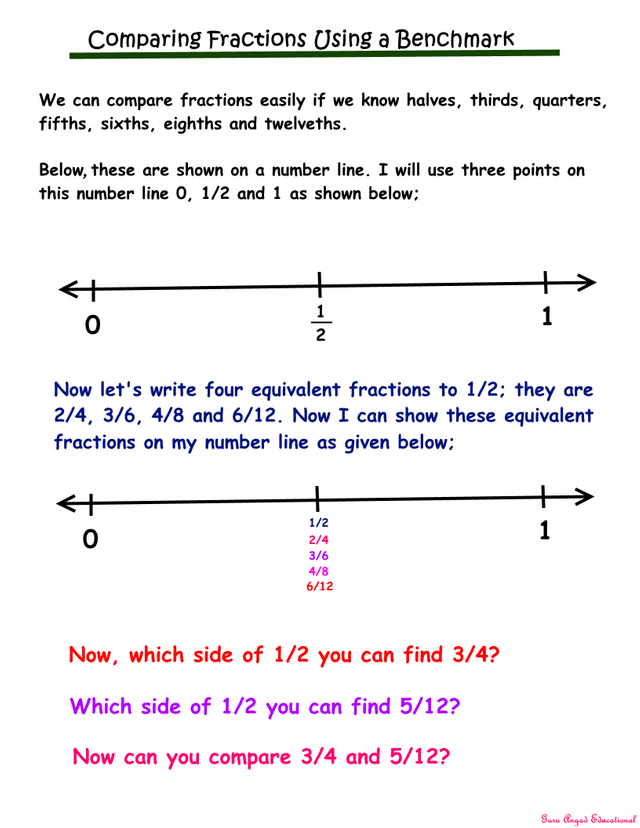
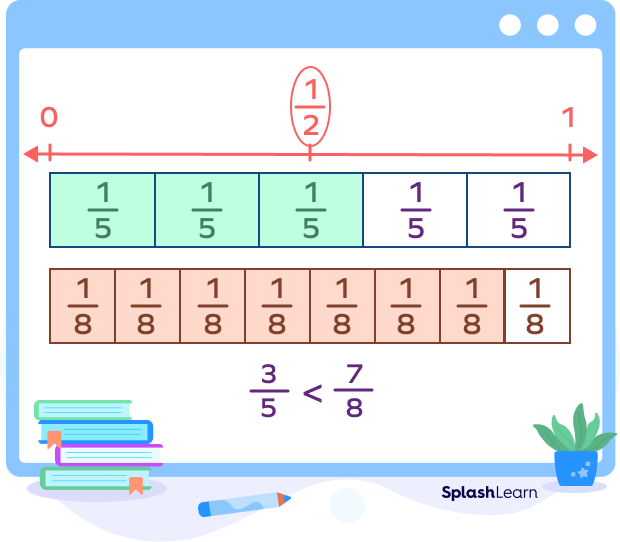
By comparing each fraction to a common benchmark, such as 1/2, you can easily determine which fraction is larger or smaller. For example, 3/5 is greater than 1/2, while 2/5 is less than 1/2, thus 3/5 is greater than 2/5.
Simplifying Calculations
Benchmark fractions can also simplify more complex mathematical operations. When adding or subtracting fractions, recognizing that certain fractions are close to benchmarks can streamline the process.
For example, when adding 7/8 and 5/8, a student might recognize that 7/8 is close to 1 and 5/8 is more than 1/2. This understanding can help them estimate the sum before performing the actual calculation.
Teaching Benchmark Fractions
Effective teaching of benchmark fractions often involves visual aids and hands-on activities. Using fraction bars, pie charts, and real-world examples helps students develop a concrete understanding of these reference points.
According to a study published in the Journal for Research in Mathematics Education, students who are taught benchmark fractions using visual representations perform better on fraction-related tasks.
Educators emphasize the importance of relating fractions to familiar contexts. For example, dividing a pizza into halves, fourths, or thirds can provide a tangible way to understand these benchmark fractions.
Impact on Everyday Life
The understanding of benchmark fractions extends far beyond the classroom. In everyday life, these concepts are essential for making informed decisions about quantities, proportions, and measurements.
Consider situations such as cooking, budgeting, or even determining discounts while shopping. A basic understanding of benchmark fractions can help you quickly estimate quantities, compare prices, and make better financial choices.
For instance, knowing that 1/3 of a cup is slightly less than 1/4 of a cup can be useful when adjusting recipes. When shopping, understanding that an item is 1/2 off can help you quickly determine the sale price.
Looking Ahead
As educational approaches continue to evolve, the significance of benchmark fractions remains constant. The ability to estimate, compare, and manipulate fractions is a foundational skill that impacts various aspects of life and learning.
Educators and curriculum developers are increasingly emphasizing the importance of incorporating real-world applications into mathematics education. This approach helps students see the relevance of benchmark fractions in their daily lives.
By fostering a strong understanding of benchmark fractions, educators can empower students to become confident and capable problem-solvers. The use of benchmark fractions promotes number sense and supports overall mathematical proficiency.