What Is Half A Quarter Of 400

The aroma of freshly baked cookies wafted through Mrs. Davison's fifth-grade classroom, a reward for tackling the week's math challenges. Pencils lay still as the students, a mix of furrowed brows and hopeful glances, waited for the final problem to be revealed. What is half a quarter of 400? It echoed through the room.

At its heart, this seemingly simple math problem, "What is half a quarter of 400?", is a gateway to understanding fundamental mathematical concepts. Mastering it strengthens arithmetic skills, promotes problem-solving abilities, and reinforces the critical link between mathematics and everyday life.

The Foundation: Unpacking the Basics

Mathematics, often perceived as a complex labyrinth, is actually built upon a series of interconnected, logical steps. Basic arithmetic operations—addition, subtraction, multiplication, and division—are the cornerstones. Each problem provides an opportunity to solidify this foundation.

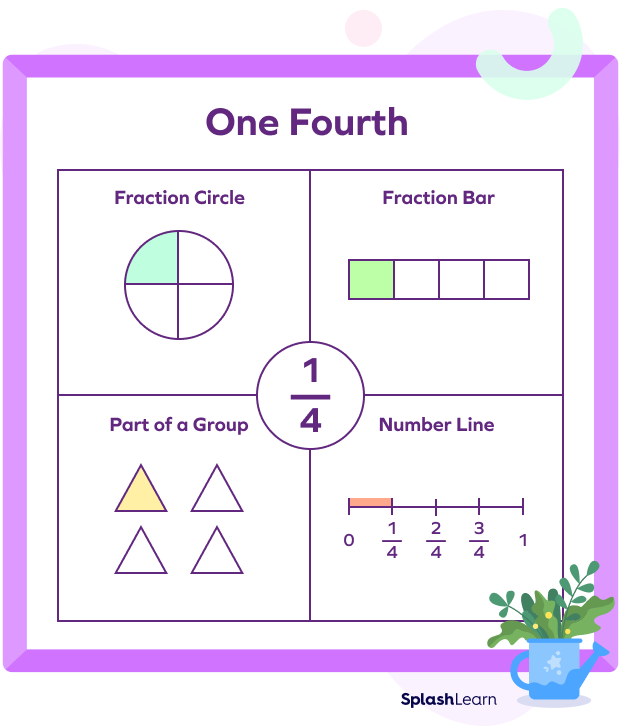
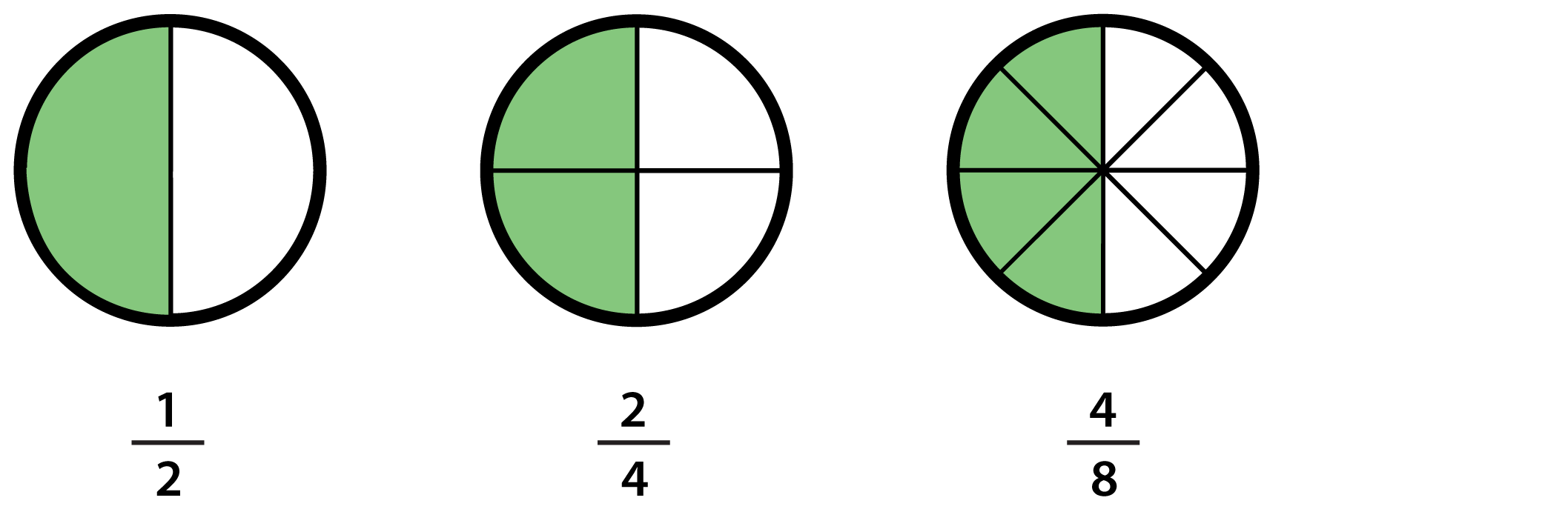
Understanding fractions is crucial. A fraction represents a part of a whole. For example, one-half (1/2) signifies one part out of two equal parts, and one-quarter (1/4) represents one part out of four equal parts.

The term "of" in math often indicates multiplication. Therefore, "a quarter of 400" means 1/4 multiplied by 400.

Deciphering the Problem

Let's break down "What is half a quarter of 400?" into smaller, manageable segments. First, we need to calculate "a quarter of 400". This requires dividing 400 by 4.

400 divided by 4 is 100. So, a quarter of 400 is 100.

The next step is to find "half of" that result. We need to calculate half of 100. This involves dividing 100 by 2.

100 divided by 2 is 50. Therefore, half a quarter of 400 is 50.

Why This Matters

This type of problem is not just about getting the right answer. It's about developing a systematic approach to problem-solving. It fosters critical thinking skills.

These fundamental skills are essential for everyday life. Whether calculating discounts at the grocery store or figuring out proportions in a recipe, the ability to apply basic math concepts is invaluable.

According to the National Council of Teachers of Mathematics (NCTM), a strong foundation in arithmetic is crucial for success in higher-level math courses. Problems like this help students build confidence and competence.

Real-World Applications

Imagine a scenario where you are sharing a pizza with friends. The pizza is cut into 8 slices (representing our "400"). You decide to only eat a quarter of the pizza.

That’s two slices. Now, you only eat half of those two slices! That’s one slice, or 50.

Consider a fundraising event. The goal is to raise $400. The organizers reach a quarter of their goal on the first day.

That means they raised $100. On the second day, they raise half of what they raised on the first day.

They would have raised $50. These examples demonstrate how these calculations translate directly into real-world situations.

Variations and Extensions

This problem can be modified to increase its complexity. For example, "What is one-third of a half of 600?" This requires an additional step of finding one-third.

Or, "What is 25% of a quarter of 800?" This introduces the concept of percentages. Converting percentages to fractions or decimals provides another layer of complexity.

Advanced students could explore algebraic representations. They could represent the problem as an equation: (1/2) * (1/4) * 400 = x.

The Importance of Practice

Consistent practice is key to mastering these mathematical concepts. Regular exercises reinforce the understanding of fractions, multiplication, and division.

Utilizing online resources, workbooks, and interactive games can make learning more engaging. Creating real-life scenarios is crucial.

Encouraging students to explain their reasoning helps solidify their understanding. It helps build communication skills.

Overcoming Challenges

Some students may struggle with the language used in the problem. The term "of" can be confusing. Clarifying its meaning in mathematical contexts is essential.

Others might find it challenging to break down the problem into smaller steps. Providing visual aids, like diagrams or manipulatives, can be helpful.

Patience and encouragement are vital. It’s essential to foster a supportive learning environment.

A Teacher's Perspective

Mrs. Johnson, a veteran math teacher, emphasizes the importance of conceptual understanding. She uses real-world examples to make math relatable.

“I always start with the basics,” she explains. “Once the students grasp the underlying concepts, they can tackle more complex problems with confidence.”

She also incorporates games and group activities to make learning fun. She believes a positive attitude towards math is crucial for success.

The Role of Parents

Parents can play a significant role in reinforcing math skills at home. Engaging children in everyday activities that involve math helps them see its relevance.

For example, while cooking, involve children in measuring ingredients. While shopping, ask them to calculate the total cost of items.

Reviewing homework together and providing encouragement can boost their confidence. Parents can create a positive attitude towards math.

Looking Ahead

Mastering fundamental mathematical concepts like these lays the groundwork for future academic success. It opens doors to various career paths.

A strong understanding of math is essential in fields such as science, technology, engineering, and mathematics (STEM). It is also important in finance and business.

By building a solid foundation in math, we empower students to become confident problem-solvers and critical thinkers. This prepares them for the challenges and opportunities of the 21st century.

The Answer, and Beyond

So, what is half a quarter of 400? The answer, as we've seen, is 50. But the true answer lies far beyond that single number. It's about understanding the process, applying critical thinking, and recognizing the power of math in our daily lives.

As Mrs. Davison’s students discovered, the sweet taste of a cookie is even sweeter when earned through a challenge well met. With each problem solved, they build not only their mathematical skills but also their confidence to tackle whatever lies ahead.

The journey through mathematics is a continuous one, filled with opportunities for growth and discovery. And sometimes, all it takes is a simple question to unlock a world of understanding.