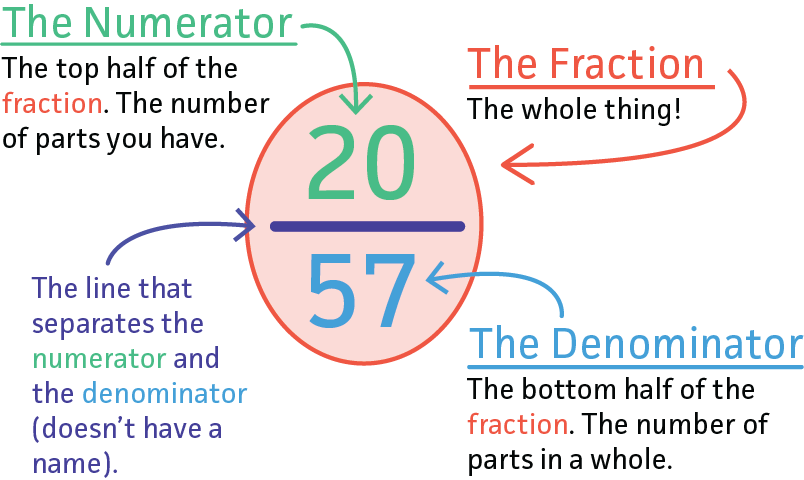
What Is The Fraction Of 28
The seemingly simple question, “What is the fraction of 28?” has sparked confusion and debate across online platforms and educational circles. While mathematically straightforward for some, the ambiguity inherent in the phrasing has led to widespread misinterpretations and diverse approaches to solving the problem.
This article aims to dissect the nuances of the question, clarifying the various interpretations and providing a comprehensive explanation of the potential answers. We will delve into the mathematical principles at play, explore the common pitfalls in understanding the question, and offer insights from educators on how to best approach such ambiguous mathematical problems.
Understanding the Ambiguity
The core of the confusion lies in the lack of context surrounding the phrase "fraction of 28." Without a specified fraction, the problem becomes open to multiple interpretations.
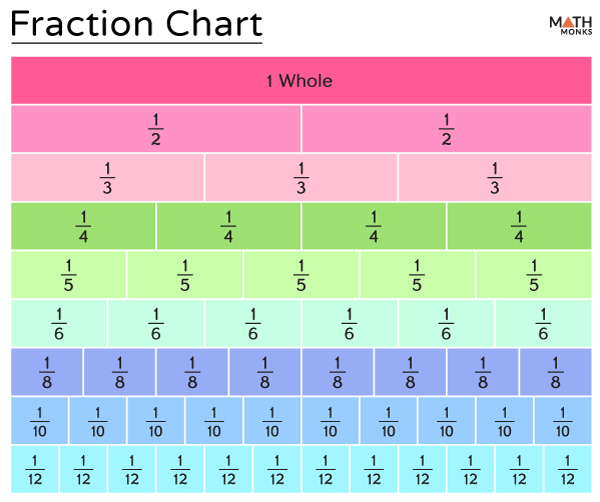
One possible interpretation is that the question is asking for a general representation of 28 as a fraction. Another is that it seeks a specific fractional part of 28, requiring an assumed or implied fraction.
28 as a Fraction: The Simplest Representation
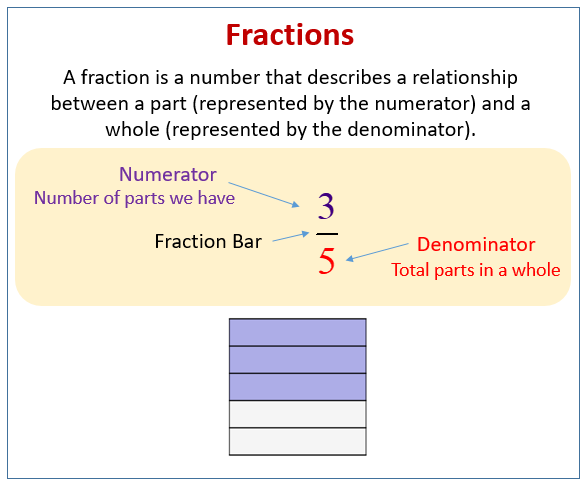
The most straightforward way to represent 28 as a fraction is 28/1. Any whole number can be expressed as a fraction by placing it over the denominator 1.
This representation maintains the value of 28 while adhering to the definition of a fraction as a ratio of two numbers. This simple answer often gets overlooked amidst more complex interpretations.
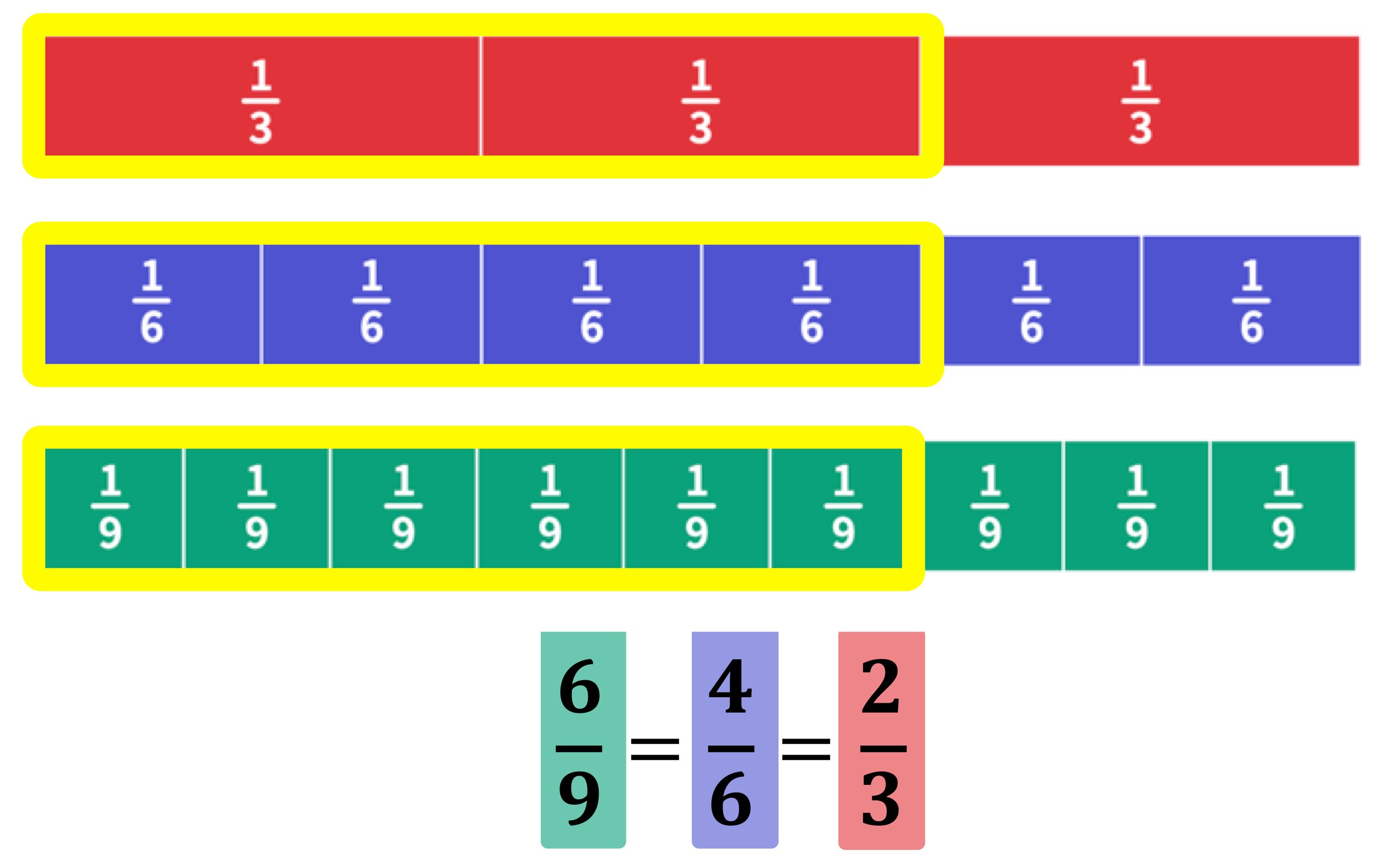
Finding a Fractional Part of 28: The Implied Fraction
Many people interpret the question as asking for a specific fractional part of 28, even without the fraction being explicitly stated. This is where the ambiguity becomes prominent.
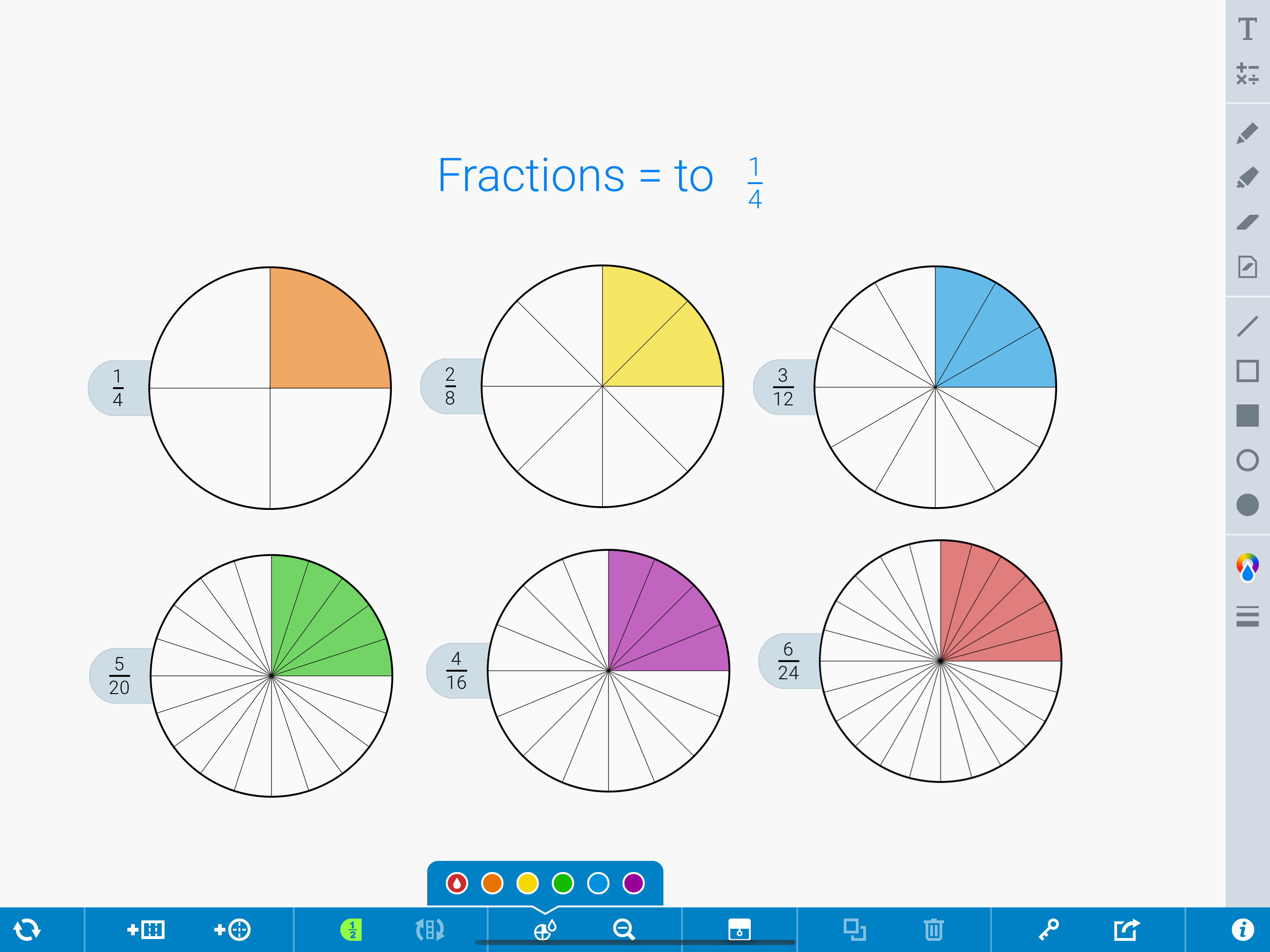
For example, if we assume the question is asking for one-half of 28, then the answer would be 14. Similarly, one-quarter of 28 is 7, and so on.
The answer completely depends on the assumed fraction, which highlights the importance of precise wording in mathematical problems.
Common Misinterpretations and Pitfalls
One common mistake is assuming the question is incomplete or has a hidden element. This leads to unnecessary complexity in attempting to solve the problem.
Another pitfall is focusing on complex fractions or advanced mathematical concepts when a simpler interpretation suffices. Overthinking the problem often obscures the most direct solution.
Students, in particular, may feel pressured to find a complicated answer, leading them down incorrect paths and creating unnecessary frustration.
The Role of Context and Precise Wording
The ambiguity surrounding the question highlights the crucial role of context in mathematical problems. Without clear context, the problem can be interpreted in multiple ways.
Precise wording is essential in mathematical problem-solving to avoid misinterpretations and ensure a unique, unambiguous solution. Ambiguity can lead to frustration and hinder effective learning.
To avoid such ambiguity, the question should be phrased as "What is one-half (or another specified fraction) of 28?" or "Express 28 as a fraction."
Expert Opinions and Educational Perspectives
Educators emphasize the importance of teaching students to identify and address ambiguity in mathematical problems. This includes developing critical thinking skills and the ability to clarify unclear questions.
"It's crucial to encourage students to ask clarifying questions when faced with an ambiguous problem," says Dr. Emily Carter, a mathematics professor at a prominent university. "This not only helps them arrive at the correct solution but also develops their problem-solving abilities."
Teaching students to break down problems into smaller, more manageable parts is also essential. This helps them identify the key elements and avoid getting overwhelmed by the overall ambiguity.
Addressing the Broader Implications
The "fraction of 28" scenario underscores a broader issue in mathematics education: the need for clear communication and problem presentation. Ambiguity can hinder learning and lead to misconceptions.
By promoting precise wording and encouraging critical thinking, educators can empower students to navigate complex mathematical problems with confidence. This also promotes a deeper understanding of the underlying mathematical concepts.
The ability to effectively communicate mathematical ideas is crucial not only in academic settings but also in various professional fields. Clear and concise problem presentation is key to success.
Looking Ahead: Fostering Clarity in Mathematics
Moving forward, educators and curriculum developers should prioritize clarity and precision in mathematical problem presentation. This includes providing sufficient context and avoiding ambiguous phrasing.
Interactive learning tools and online resources can be valuable in reinforcing these principles. These tools can provide students with opportunities to practice clarifying ambiguous problems and developing their critical thinking skills.
By fostering a culture of clarity and encouraging students to question assumptions, we can create a more effective and engaging mathematics learning environment for all.
Ultimately, the "fraction of 28" debate serves as a valuable reminder of the importance of clear communication and critical thinking in mathematics. By embracing these principles, we can empower students to approach mathematical problems with confidence and achieve a deeper understanding of the subject.