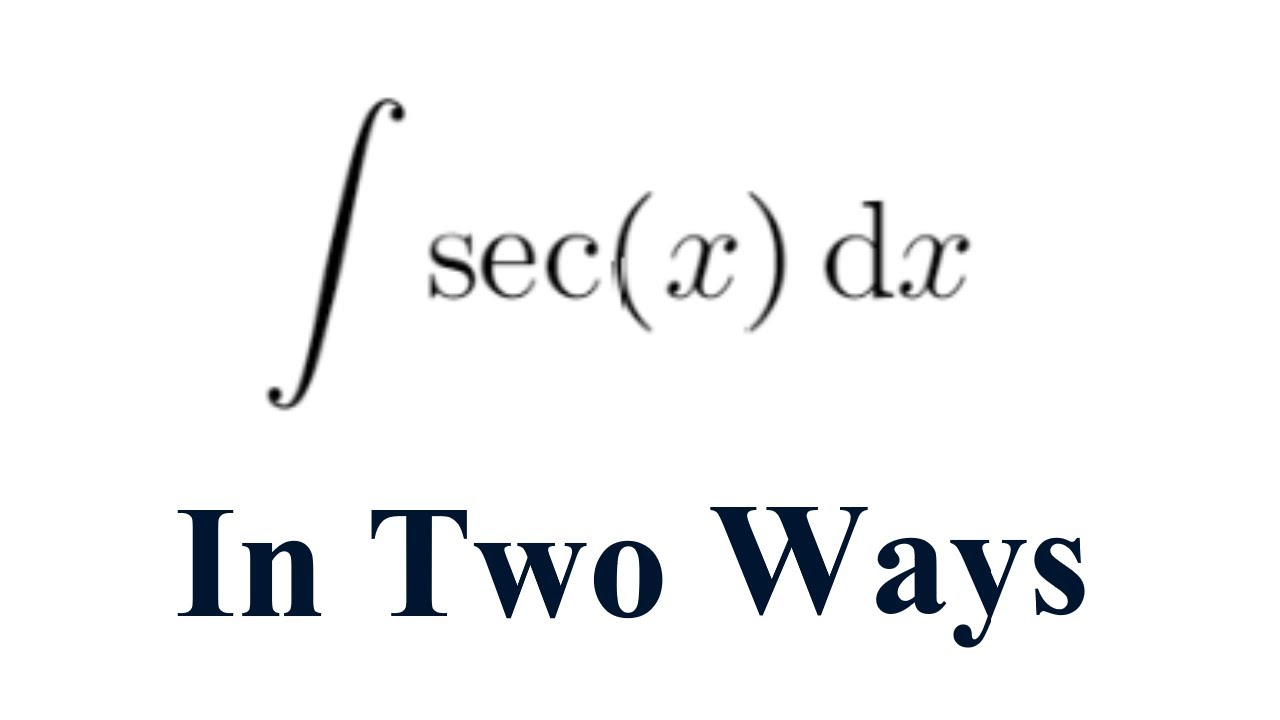What Is The Integral Of Sec
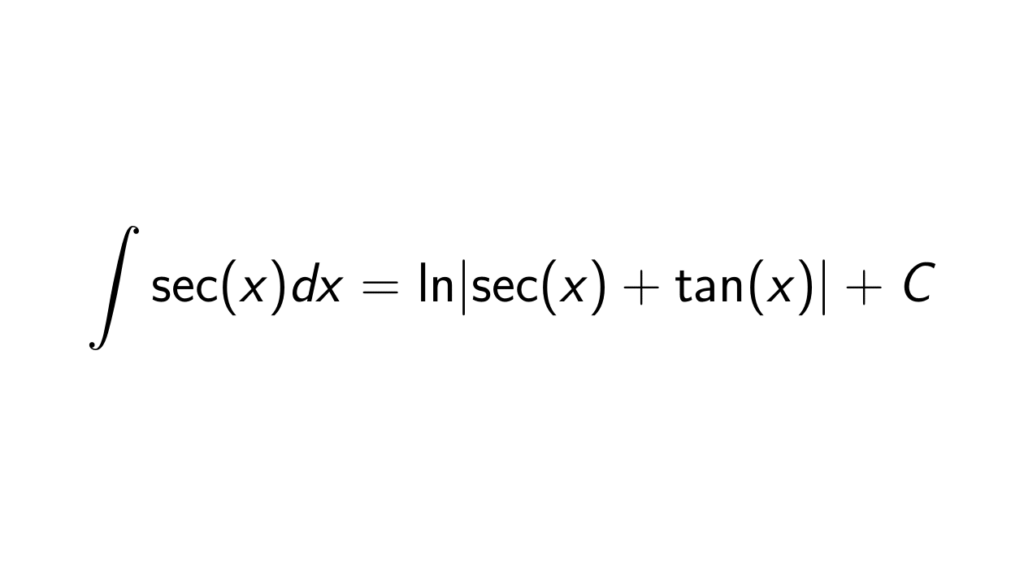
Imagine you're a sailor charting a course across the vast ocean. The sun glints off the waves, each rise and fall a small, rhythmic pulse against the hull of your ship. But you need to know more than just the immediate undulation; you need to understand the cumulative effect, the overall distance traveled along a curved path – the very essence of integration. In mathematics, much like navigation, we often seek to understand the total effect of continuous change, a concept beautifully illustrated by the integral of the secant function.
At its heart, the integral of sec(x), denoted as ∫sec(x) dx, is a seemingly simple question with a surprisingly elegant and insightful answer: ln|sec(x) + tan(x)| + C. This formula reveals more than just a mathematical solution; it unveils a deeper connection between trigonometric functions and the natural logarithm, showcasing the intricate tapestry of mathematical relationships. The " + C" signifies the constant of integration, a crucial reminder that there are infinitely many antiderivatives that differ only by a constant value.
A Journey Through Trigonometry
To truly appreciate the integral of secant, we must first understand its origins within the realm of trigonometry. The secant function, sec(x), is defined as the reciprocal of the cosine function, i.e., sec(x) = 1/cos(x). It's one of the six fundamental trigonometric functions, along with sine, cosine, tangent, cotangent, and cosecant.
These functions describe the relationships between the angles and sides of a right triangle. They are essential in various fields, from physics and engineering to computer graphics and music theory. Their cyclical nature makes them indispensable in modeling periodic phenomena like waves, oscillations, and rotational motion.
The Challenge of Integration
While the derivatives of trigonometric functions are relatively straightforward, their integrals can be more challenging. The integral of secant is notoriously difficult to derive using basic integration techniques. It requires a clever trick – multiplying both the numerator and denominator of sec(x) by (sec(x) + tan(x)).
This seemingly arbitrary step transforms the integral into a form that can be solved using a u-substitution. Let u = sec(x) + tan(x), then du = (sec(x)tan(x) + sec2(x)) dx. Substituting these values into the modified integral allows us to rewrite it in terms of u, making the integration process significantly easier.
The derivation, though elegant, is not immediately obvious, highlighting the importance of mathematical ingenuity. It demonstrates that sometimes the most profound solutions arise from unexpected transformations. This technique is a testament to the creative problem-solving skills inherent in mathematical exploration.
Unveiling the Solution
After applying the multiplication trick and the u-substitution, the integral transforms into ∫(1/u) du, a familiar form that integrates to ln|u| + C. Substituting back u = sec(x) + tan(x), we arrive at the final solution: ∫sec(x) dx = ln|sec(x) + tan(x)| + C. This formula represents the area under the curve of the secant function.
The absolute value signs ensure that the argument of the logarithm is always positive, as the natural logarithm is only defined for positive values. This is a subtle but important detail, ensuring the mathematical rigor of the solution. The constant of integration, 'C', represents the family of antiderivatives.
Beyond the Formula: Its Significance
The integral of secant is more than just a formula to memorize; it holds significant implications in various areas of mathematics and its applications. It appears in the calculations of arc lengths of curves, particularly those defined by trigonometric functions. Understanding this integral is crucial for solving problems in calculus involving the geometry of curves.
In physics, the integral of secant plays a role in certain models involving wave propagation and electromagnetic fields. Its application extends to areas where trigonometric functions describe cyclical behaviors or geometric relationships. The integral's presence in these models underscores the interconnectedness of mathematical concepts and their relevance to real-world phenomena.
Furthermore, the derivation of the integral of secant serves as an excellent example of mathematical problem-solving techniques. The clever trick of multiplying by (sec(x) + tan(x)) highlights the importance of creativity and insight in mathematical discovery. It's a valuable lesson in how seemingly insurmountable problems can be overcome with ingenuity.
A Reflection on Mathematical Beauty
The journey to understanding the integral of secant is a testament to the beauty and elegance of mathematics. It's a reminder that even seemingly complex problems can be unraveled with the right tools and a bit of ingenuity. The integral’s existence highlights the interconnectedness of mathematical concepts.
From its trigonometric foundations to its logarithmic solution, the integral of secant exemplifies the power of mathematical reasoning. It showcases how seemingly disparate concepts can come together to form a harmonious and insightful whole. The formula's simplicity belies the depth and complexity of its derivation.
So, the next time you encounter the integral of sec(x), remember that it's more than just a formula. It is a symbol of mathematical ingenuity, a bridge between trigonometry and logarithms, and a testament to the enduring beauty of mathematical exploration. Just as a sailor uses mathematical principles to navigate the seas, we can use this integral to chart our course through the vast landscape of mathematical knowledge.