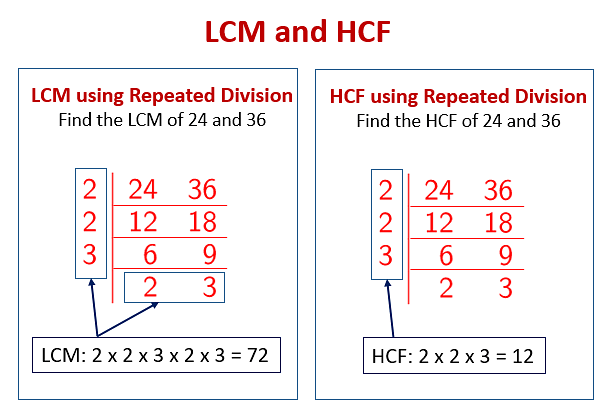
What Is The Lcm Of 14 And 10

Imagine a world where numbers dance, not in complex equations, but in harmonious rhythms. Think of two musical notes, 14 and 10, each with its own unique beat. Now, picture them seeking a shared pulse, a common ground where their rhythms meet and resonate.
This shared pulse, in the language of mathematics, is the Least Common Multiple (LCM). Today, we'll journey into the realm of numbers to discover the LCM of 14 and 10, unraveling the mystery behind this fundamental concept.
Decoding the Least Common Multiple
The Least Common Multiple, or LCM, is the smallest positive integer that is perfectly divisible by two or more numbers. It's like finding the smallest possible meeting point for the multiples of those numbers.
To find the LCM of 14 and 10, we need to explore their multiples. Let's begin by listing the multiples of each number.
Unveiling Multiples
The multiples of 14 are: 14, 28, 42, 56, 70, 84, 98, 112, and so on. Each number is obtained by successively adding 14 to the previous one.
Similarly, the multiples of 10 are: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, and so on. Here, we add 10 repeatedly.
Looking at both lists, we can identify common multiples: 70, 140, and so on. However, we seek the least common multiple.
Finding the Smallest Intersection
Among the common multiples we found, 70 is the smallest. Therefore, the LCM of 14 and 10 is 70.
This means that 70 is the smallest number that both 14 and 10 divide into without leaving a remainder. It's their first shared landing point in the infinite sequence of multiples.
Methods to Calculate LCM
While listing multiples works for smaller numbers, it becomes less practical for larger values. Fortunately, there are other methods to determine the LCM more efficiently.
Prime Factorization: A Deeper Dive
Prime factorization is a powerful technique to break down a number into its prime constituents. A prime number is a number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11).
Let's factorize 14 and 10 into their prime factors. 14 can be expressed as 2 x 7, and 10 can be expressed as 2 x 5.
To find the LCM using prime factorization, we take the highest power of each prime factor present in either number. In this case, we have 2, 5, and 7. The LCM is thus 2 x 5 x 7 = 70.
Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF), is the largest number that divides two or more numbers without leaving a remainder. There's a relationship between the LCM and GCD.
The formula is: LCM(a, b) = (|a * b|) / GCD(a, b). First, we need to find the GCD of 14 and 10.
The divisors of 14 are: 1, 2, 7, and 14. The divisors of 10 are: 1, 2, 5, and 10. The greatest common divisor is 2.
Applying the formula, LCM(14, 10) = (14 * 10) / 2 = 140 / 2 = 70. We arrive at the same answer using this method.
The Significance of LCM
The concept of LCM is not merely a mathematical exercise; it has significant applications in various fields. From everyday problem-solving to advanced scientific calculations, the LCM plays a crucial role.
In mathematics, the LCM is essential for adding or subtracting fractions with different denominators. It provides the common denominator needed to perform the operations.
In real-world scenarios, the LCM helps us solve problems involving repeating events. For example, imagine two buses leaving a station at different intervals. The LCM can determine when they will next leave together.
Applications in Diverse Fields
Beyond basic arithmetic, the LCM finds its use in areas like music and engineering. In music, understanding LCM helps in synchronizing rhythms and creating harmonious compositions.
In engineering, particularly in mechanical systems, the LCM is vital for designing gears and ensuring smooth operations. Engineers use it to calculate gear ratios and optimize performance.
Even in computer science, the LCM can be applied in scheduling tasks and managing resources efficiently. It helps in synchronizing processes that occur at different frequencies.
A Fundamental Concept
The LCM is a foundational element in mathematics that underpins many other concepts. Mastery of LCM is essential for building a strong mathematical base.
Understanding how to find and apply the LCM enhances problem-solving skills. It fosters logical thinking and analytical abilities.
Therefore, grasping the essence of LCM is not just about memorizing formulas, but about understanding its significance and applications.
Conclusion: Harmony in Numbers
Our exploration of the LCM of 14 and 10 reveals the beauty and practicality of this mathematical concept. The answer, 70, is more than just a number. It's a point of convergence, a shared harmony between two distinct numerical rhythms.
Whether you're a student, a professional, or simply curious about the world around you, understanding the LCM can unlock a new appreciation for the elegance of mathematics.
So, next time you encounter numbers, remember their potential for harmony, and consider the shared rhythm they might create. Like musical notes finding their common beat, numbers, too, can dance together in perfect unison.





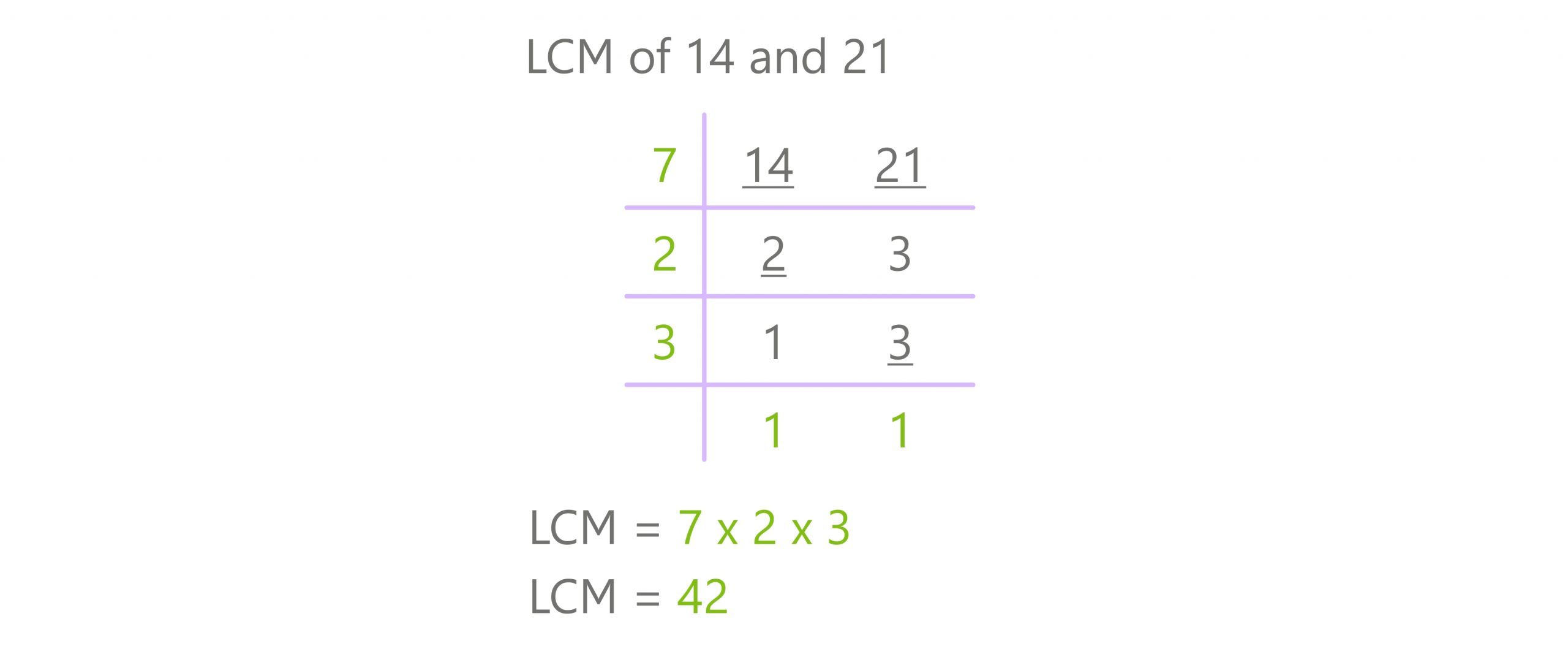
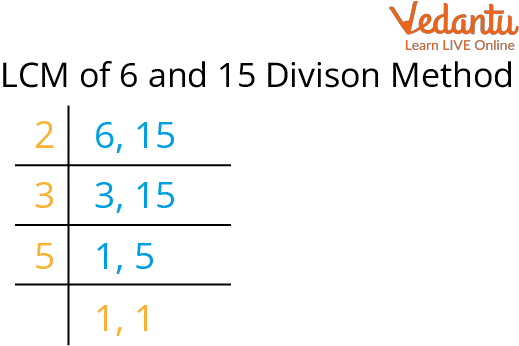
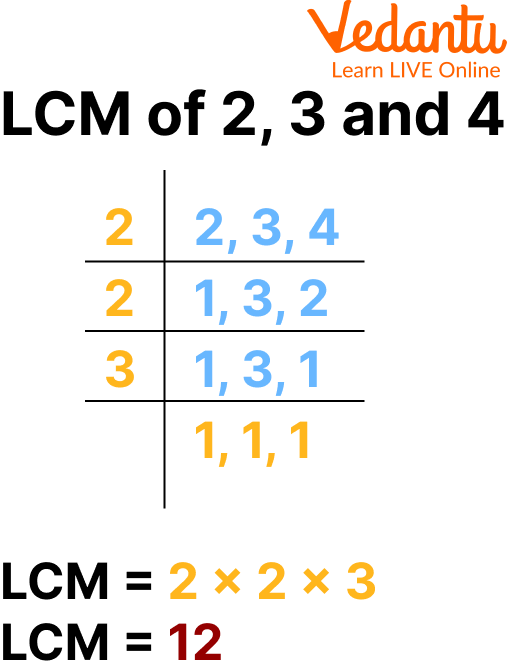


/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)