What Is The Lcm Of 14 And 18

In elementary mathematics, students often encounter the concept of the Least Common Multiple (LCM). While seemingly simple, understanding the LCM is crucial for mastering more complex arithmetic operations, particularly when dealing with fractions and ratios.

The question of determining the LCM of 14 and 18 serves as a foundational example. It highlights the process of identifying the smallest multiple that both numbers share. This process reinforces core mathematical principles.

Understanding the Least Common Multiple

The LCM, or Least Common Multiple, is the smallest positive integer that is perfectly divisible by two or more numbers. It's a fundamental concept in number theory. It has practical applications in various mathematical problems, including simplifying fractions and solving algebraic equations.

Methods for Finding the LCM

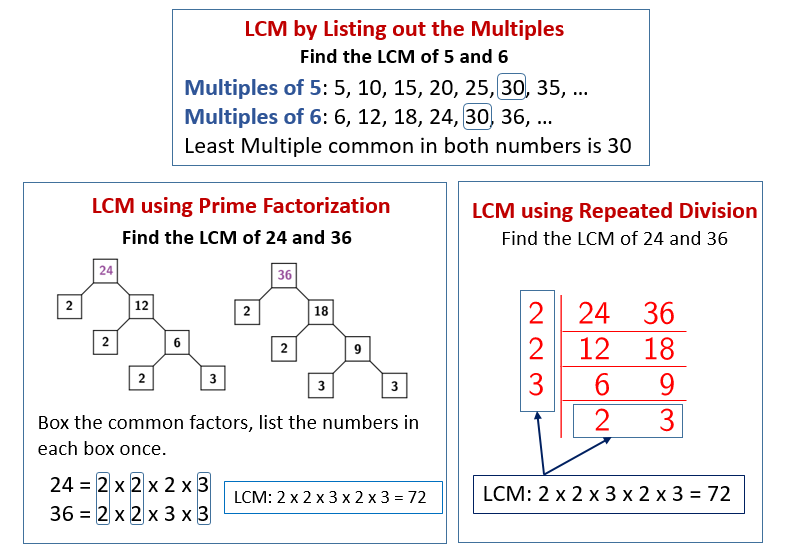
There are several methods to find the LCM of two numbers. Two common techniques are the prime factorization method and the listing multiples method. Understanding both provides a comprehensive approach.

Prime factorization involves breaking down each number into its prime factors. Then, the LCM is found by multiplying the highest powers of all prime factors present in either number.

Listing multiples involves writing out the multiples of each number until a common multiple is found. The smallest such multiple is the LCM.

Calculating the LCM of 14 and 18

Let's apply both methods to find the LCM of 14 and 18.

Using the prime factorization method, we first find the prime factors of each number. 14 is 2 x 7 and 18 is 2 x 3 x 3 or 2 x 3².

The LCM is then the product of the highest powers of all prime factors present: 2 x 3² x 7. This equals 2 x 9 x 7, which simplifies to 126.

Alternatively, we can list the multiples of 14 and 18. Multiples of 14 include: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140... Multiples of 18 include: 18, 36, 54, 72, 90, 108, 126, 144...

The smallest common multiple in both lists is 126. Therefore, the LCM of 14 and 18 is 126.

Significance and Applications

Understanding the LCM extends beyond simple calculations. It’s critical for various practical applications in mathematics and everyday life.

For instance, when adding or subtracting fractions with different denominators, the LCM is used to find a common denominator. This allows for the fractions to be combined easily.

Consider adding 1/14 and 1/18. The LCM, 126, becomes the common denominator. The fractions are then rewritten as 9/126 and 7/126 respectively, allowing for straightforward addition.

Beyond fractions, LCM finds uses in scheduling problems. Consider tasks that occur at regular intervals. The LCM helps determine when they will occur simultaneously.

Potential Impact on Learners

Mastering the LCM is a building block for more advanced mathematical concepts. A solid understanding allows students to progress smoothly in their mathematical education.

Struggling with LCM can hinder the understanding of fractions, ratios, and other related topics. This underscores the importance of early mastery.

Educators emphasize the importance of hands-on activities and real-world examples to enhance understanding. These help students grasp the concept's relevance.

Conclusion

In summary, the Least Common Multiple of 14 and 18 is 126. This result is achieved using either the prime factorization method or the listing multiples method.

Understanding the LCM is essential for success in various mathematical domains. It provides a foundation for advanced problem-solving.

Continuous practice and application of this concept are crucial for solidifying understanding. This benefits learners in their academic journey.