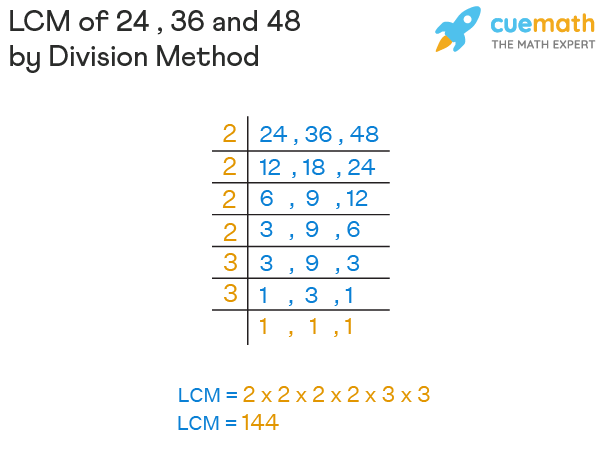What Is The Lcm Of 18 And 21

The question "What is the Least Common Multiple (LCM) of 18 and 21?" might seem like a simple math problem, but its understanding forms a foundational concept in various fields, from scheduling to music theory. This seemingly elementary query has surprisingly broad applications.
The LCM, by definition, is the smallest positive integer that is perfectly divisible by two or more numbers. In essence, knowing how to calculate the LCM helps in finding the smallest common ground between multiples of different numbers.
Understanding the Least Common Multiple
The LCM of 18 and 21 is 126. This means that 126 is the smallest number that both 18 and 21 divide into without leaving a remainder.
Methods for Calculating the LCM
There are several methods to calculate the LCM. Two common approaches include the prime factorization method and the listing multiples method.
The prime factorization method involves breaking down each number into its prime factors. For 18, the prime factors are 2 x 3 x 3 (or 2 x 3²). For 21, the prime factors are 3 x 7.
To find the LCM, you take the highest power of each prime factor that appears in either factorization and multiply them together. This results in 2 x 3² x 7 = 2 x 9 x 7 = 126.
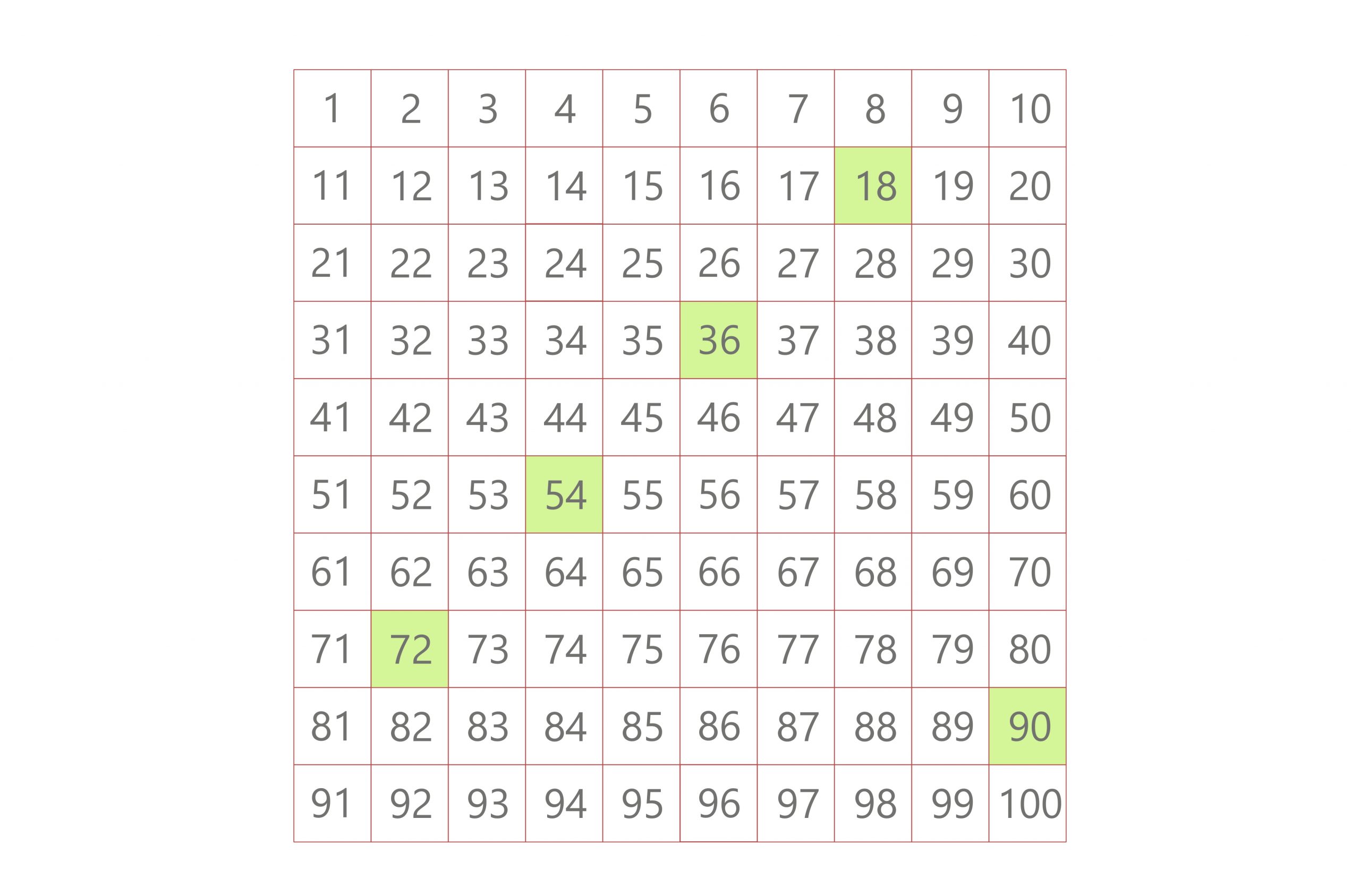
The listing multiples method involves listing the multiples of each number until you find a common multiple. Multiples of 18 include 18, 36, 54, 72, 90, 108, 126, etc. Multiples of 21 include 21, 42, 63, 84, 105, 126, etc.
As you can see, the first common multiple in both lists is 126, confirming our calculation using the prime factorization method.
Why Is This Important?
While seemingly simple, understanding the LCM is essential in numerous practical scenarios. For instance, consider scheduling events or tasks that occur at different intervals.
Imagine a scenario where a bus route runs every 18 minutes and another runs every 21 minutes. The LCM of 18 and 21 (which is 126) tells you when both buses will arrive at the same stop simultaneously – every 126 minutes.
This principle applies in various logistical scenarios, such as coordinating deliveries, aligning project timelines, and even in more abstract areas like music theory where rhythmic patterns and harmony often rely on understanding multiples and common intervals.
The Broader Context of Mathematical Literacy
The ability to understand and calculate the LCM is also a building block for more advanced mathematical concepts. It's used in simplifying fractions, solving algebraic equations, and even in computer science for optimizing algorithms.
Mathematical literacy, in general, is increasingly crucial in a data-driven world. Basic concepts like the LCM are the foundation upon which more complex understanding is built.
In a report released by the National Center for Education Statistics (NCES), proficiency in mathematics is a key indicator of academic success and future career prospects. Even seemingly simple calculations contribute to a broader understanding of mathematical principles.
Human Interest Angle: A Real-World Example
Consider a baker who wants to create identical batches of cookies using two different recipes. One recipe yields 18 cookies and the other yields 21. To ensure each batch contains the same number of cookies, the baker needs to figure out how many times to multiply each recipe.
The baker would use the LCM (126) to find the common multiple. She needs to make seven batches of the first recipe (126 / 18 = 7) and six batches of the second recipe (126 / 21 = 6). This way, she'll have 126 cookies from each recipe, allowing her to create perfectly matching batches.
This relatable scenario demonstrates that even seemingly abstract math concepts have practical, real-world applications that impact everyday life.
Conclusion
The answer to "What is the LCM of 18 and 21?" is 126. While the answer itself is a single number, its significance extends far beyond a simple calculation.
Understanding the LCM is a valuable tool for problem-solving in various aspects of life, from scheduling to cooking. Furthermore, it serves as a critical foundation for more complex mathematical understanding.
By mastering fundamental mathematical concepts, individuals are better equipped to navigate the complexities of the modern world.







/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)