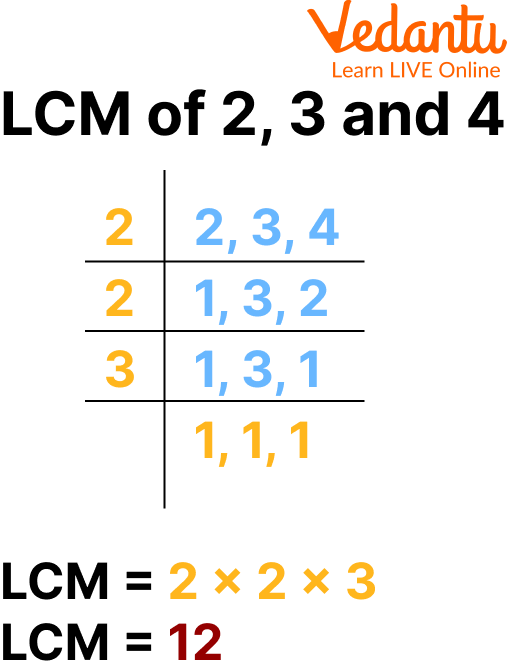What Is The Lcm Of 20 And 12

Imagine a classroom buzzing with youthful energy, pencils scratching against paper, and a gentle murmur of numbers being crunched. Mrs. Davis, a teacher with a twinkle in her eye and years of experience under her belt, poses a question that seems simple on the surface, yet holds a fundamental key to mathematical understanding: "What is the LCM of 20 and 12?"
The answer, 60, isn't just a number; it's a bridge that connects fractions, simplifies problem-solving, and unlocks patterns in the world around us.
This article delves into the concept of the Least Common Multiple (LCM), using the specific example of 20 and 12 as a starting point to explore its broader significance in mathematics and everyday life.
Understanding the Basics: What is LCM?
The Least Common Multiple, or LCM, is the smallest positive integer that is perfectly divisible by two or more given numbers.
Think of it as finding the smallest meeting point on a number line where multiples of the given numbers converge.
Finding the LCM of 20 and 12: A Step-by-Step Approach
Let's break down how to find the LCM of 20 and 12 using a couple of different methods.
This will clarify the underlying principles and demonstrate the versatility of mathematical tools.
Method 1: Listing Multiples
One straightforward way to find the LCM is by listing the multiples of each number until you find a common one.
Multiples of 20: 20, 40, 60, 80, 100...
Multiples of 12: 12, 24, 36, 48, 60, 72...
As you can see, 60 appears in both lists, and it's the smallest number they share.
Therefore, the LCM of 20 and 12 is 60.
Method 2: Prime Factorization
Another method involves prime factorization, which breaks down each number into its prime factors.
Prime factorization of 20: 2 x 2 x 5 (or 22 x 5)
Prime factorization of 12: 2 x 2 x 3 (or 22 x 3)
To find the LCM, take the highest power of each prime factor that appears in either factorization and multiply them together: 22 x 3 x 5 = 4 x 3 x 5 = 60.
Again, the LCM of 20 and 12 is 60.
Why is LCM Important?
The concept of LCM might seem abstract, but it has practical applications in various areas of mathematics and beyond.
Understanding its importance helps solidify its place in our mathematical toolkit.
Fractions and Common Denominators
One of the most common applications of LCM is in working with fractions.
To add or subtract fractions, they need to have a common denominator.
The LCM of the denominators serves as the least common denominator, simplifying the process.
For instance, if you need to add 1/20 and 1/12, you would use 60 as the common denominator, resulting in 3/60 + 5/60 = 8/60, which can then be simplified.
Real-World Applications
LCM also appears in everyday scenarios.
Consider scheduling: If one event happens every 20 days and another happens every 12 days, the LCM (60 days) tells you when they will coincide again.
This principle applies to tasks like synchronizing schedules, planning deliveries, or even understanding cyclical events.
"Understanding LCM is not just about memorizing a formula; it's about grasping a fundamental concept that unlocks problem-solving abilities in various contexts," says Dr. Emily Carter, a mathematics professor at Stanford University.
Delving Deeper: Beyond the Basics
While we've established the fundamentals, there's more to explore regarding LCM and its connections to other mathematical ideas.
Relationship with Greatest Common Divisor (GCD)
The LCM is closely related to the Greatest Common Divisor (GCD), also known as the Highest Common Factor (HCF).
The GCD is the largest number that divides evenly into two or more numbers.
There's a formula that connects LCM and GCD: LCM(a, b) x GCD(a, b) = a x b.
In the case of 20 and 12, the GCD is 4, and using the formula, LCM(20, 12) x 4 = 20 x 12, which simplifies to LCM(20, 12) = (20 x 12) / 4 = 60.
Applications in Computer Science
LCM finds applications in computer science, particularly in areas like data synchronization and scheduling algorithms.
For example, in managing tasks with different periodicities, the LCM can help determine optimal synchronization points to minimize conflicts and ensure efficient resource allocation.
Understanding these applications demonstrates the interdisciplinary nature of mathematical concepts.
Conclusion: The Enduring Significance of LCM
The answer to the question, "What is the LCM of 20 and 12?" is more than just a number; it's an entry point into a world of mathematical connections and practical applications.
From simplifying fractions to scheduling events, the concept of LCM provides a valuable tool for problem-solving in diverse fields.
As Mrs. Davis's students discover, mastering LCM isn't just about acing a math test; it's about developing a deeper understanding of the patterns and relationships that govern the world around us.








/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)