What Is The Lcm Of 8 And 24

Imagine a classroom, sunlight streaming through the windows, illuminating a group of children huddled around a whiteboard. Markers dance across the surface, sketching numbers and symbols, a collaborative puzzle taking shape. The air buzzes with a mixture of focused concentration and the occasional burst of excited chatter as they delve into a fundamental concept: the least common multiple.
At its core, the question "What is the LCM of 8 and 24?" delves into the realm of number theory, a foundational pillar of mathematics. Understanding the Least Common Multiple (LCM) is essential for simplifying fractions, solving algebraic equations, and even understanding rhythmic patterns in music.
Unveiling the LCM: The Basics
The Least Common Multiple, or LCM, is the smallest positive integer that is perfectly divisible by two or more given numbers. It’s a concept that builds upon the understanding of multiples and divisibility rules.
To find the LCM of 8 and 24, we are searching for the smallest number that both 8 and 24 can divide into without leaving a remainder.
Methods for Finding the LCM
There are several methods to calculate the LCM, each offering a slightly different approach to the problem. Let's explore some of the most common and effective techniques.
Listing Multiples
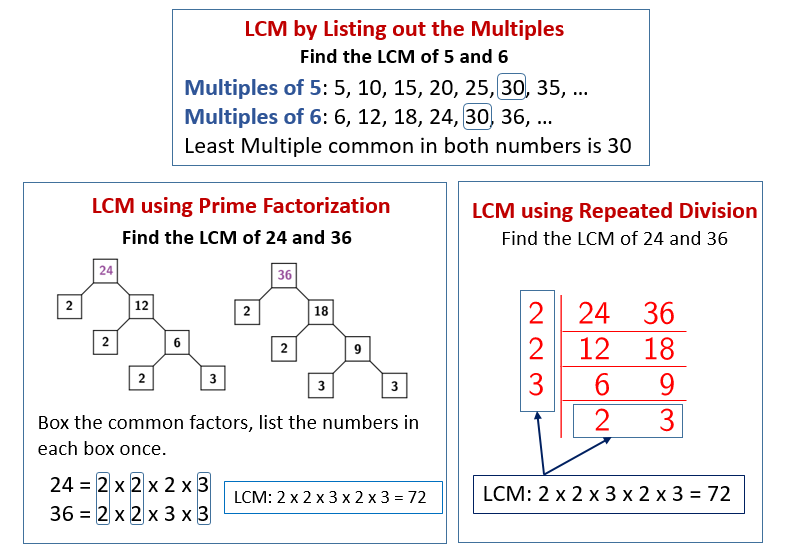
One straightforward method involves listing the multiples of each number until a common multiple is found. This method works well for smaller numbers.
Multiples of 8: 8, 16, 24, 32, 40...
Multiples of 24: 24, 48, 72...
As we can see, the smallest multiple that appears in both lists is 24. Therefore, the LCM of 8 and 24 is 24.
Prime Factorization
The prime factorization method is a more systematic approach, particularly useful for larger numbers. This involves breaking down each number into its prime factors.
The prime factorization of 8 is 2 x 2 x 2, or 23. The prime factorization of 24 is 2 x 2 x 2 x 3, or 23 x 3.
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either number. In this case, we have 23 and 31.
The LCM is then the product of these highest powers: 23 x 31 = 8 x 3 = 24.
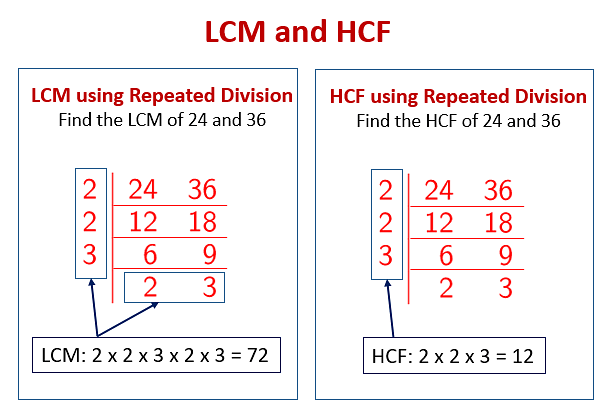
The Division Method
The division method involves dividing both numbers by their common prime factors until we are left with 1. Then, we multiply all the divisors together to find the LCM.
First, divide both 8 and 24 by their common factor 2: 8/2 = 4, 24/2 = 12. Then, divide again by 2: 4/2 = 2, 12/2 = 6. Finally, divide one more time by 2: 2/2 = 1, 6/2 = 3.
Then we divide 3 by 3, getting 1. Multiplying all the divisors together (2 x 2 x 2 x 3) gives us 24, confirming that the LCM of 8 and 24 is indeed 24.
Why is the LCM of 8 and 24 equal to 24?
The reason the LCM of 8 and 24 is 24 lies in the fact that 24 is a multiple of 8. This simplifies the process significantly.
Since 24 is divisible by 8 (24 / 8 = 3), 24 is already a common multiple of both numbers. Therefore, it automatically becomes the *least* common multiple.
Real-World Applications of LCM
While the concept of LCM might seem abstract, it has numerous practical applications in everyday life. From scheduling events to understanding gear ratios, the LCM plays a crucial role.
Consider a scenario where two buses leave a station. One bus leaves every 8 minutes, and another leaves every 24 minutes. To determine when they will both leave the station at the same time, you would calculate the LCM of 8 and 24, which is 24 minutes. This illustrates how LCM helps in determining synchronized events.
In music, the LCM can be used to understand rhythmic patterns. If one instrument plays a note every 8 beats and another plays a note every 24 beats, the LCM tells you how many beats until they play together.
The Significance of Number Theory
Understanding concepts like the LCM is fundamental to a broader understanding of number theory. Number theory is a branch of mathematics that deals with the properties and relationships of numbers, particularly integers.
From cryptography to computer science, number theory forms the backbone of many technological advancements. The study of prime numbers, divisibility, and modular arithmetic all fall under this umbrella.
By grasping the basics of LCM, you’re laying a foundation for more complex mathematical concepts. These concepts are essential for further studies in fields like algebra, calculus, and beyond.
Conclusion: A Building Block for Mathematical Understanding
The question "What is the LCM of 8 and 24?" may seem simple, but it unlocks a deeper understanding of fundamental mathematical principles. The answer, 24, is more than just a number; it represents a core concept that underlies many real-world applications.
By mastering the art of finding the LCM, individuals gain a valuable tool for problem-solving and critical thinking. The ability to identify patterns, analyze relationships, and apply mathematical concepts to everyday situations becomes greatly enhanced.
So, the next time you encounter the LCM, remember that you’re not just crunching numbers. You’re building a strong foundation for mathematical understanding and opening doors to a world of exciting possibilities.









/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)