What Is The Phase Shift Of A Periodic Function

Imagine a serene ocean, waves rising and falling in a rhythmic dance. Now picture another wave, identical in shape and size, but slightly out of sync. One crests a moment later than the other. This subtle difference, this offset in their timing, is akin to what we call phase shift in the mathematical world of periodic functions. It's a concept that might sound intimidating at first, but it's surprisingly intuitive and fundamental to understanding the behavior of many phenomena around us.
At its core, the phase shift of a periodic function quantifies how much a wave is shifted horizontally with respect to a reference wave. Understanding phase shift is crucial in fields ranging from physics and engineering to music and even economics, allowing us to predict and analyze repetitive patterns with greater accuracy.
The Fundamentals of Periodic Functions
Before diving into phase shift, let’s refresh our understanding of periodic functions. A periodic function is simply a function that repeats its values at regular intervals.
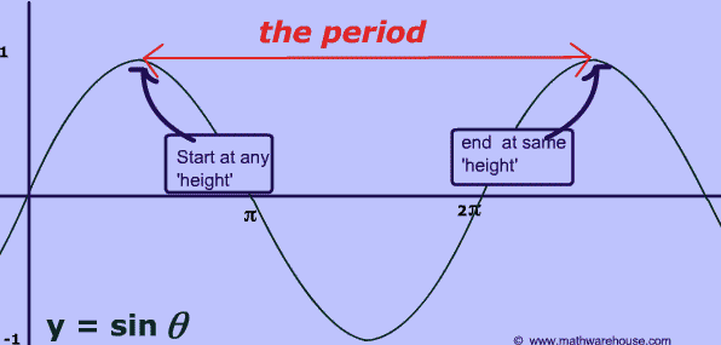
Think of a swing set: it moves back and forth in a predictable, repeating pattern. Similarly, the sine wave, a cornerstone of mathematics, oscillates continuously between -1 and 1, completing a full cycle every 2π radians.
Mathematically, a function f(x) is periodic if there exists a non-zero constant P such that f(x + P) = f(x) for all values of x. This constant P is called the period of the function.
Introducing Phase Shift
Now, consider two identical sine waves. If one wave starts its cycle a little later than the other, we say it has a phase shift.
Formally, the phase shift is the amount by which the input to the function is shifted horizontally. It’s often represented by the Greek letter φ (phi).
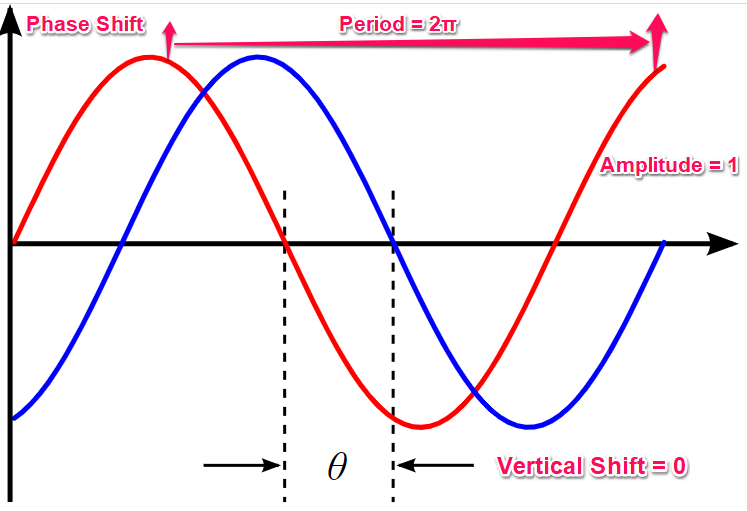
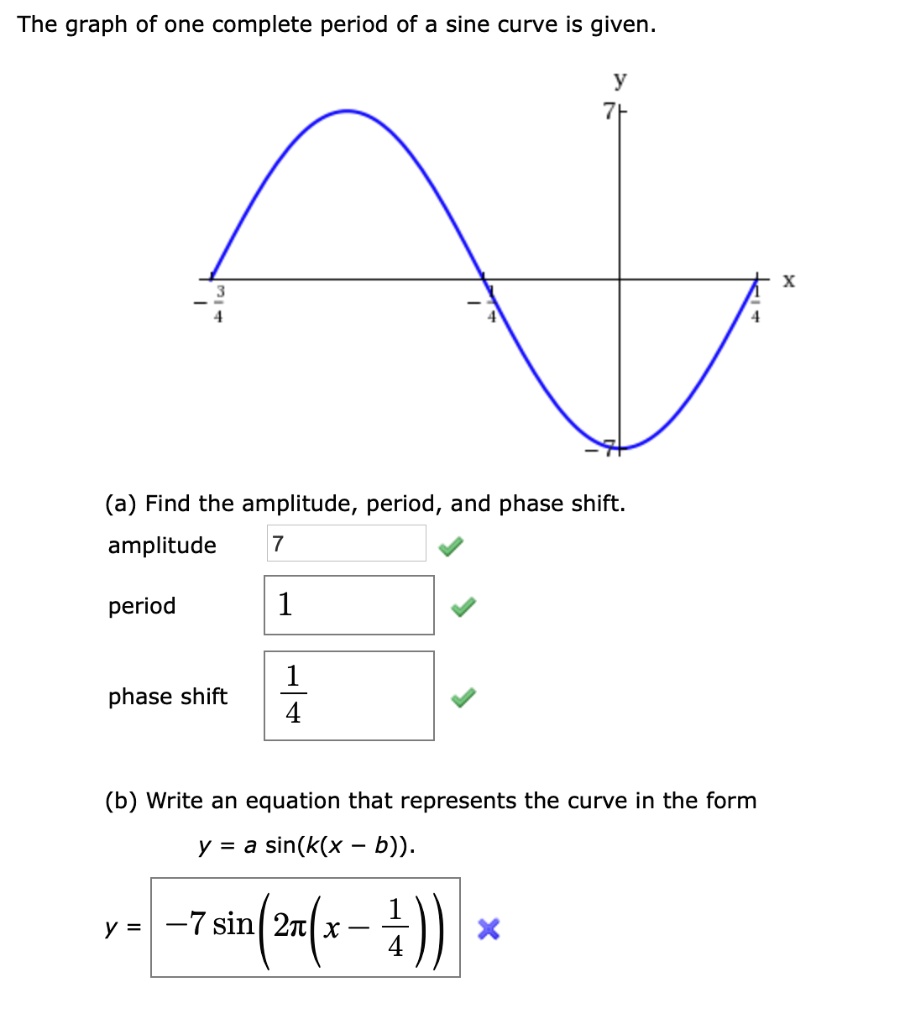
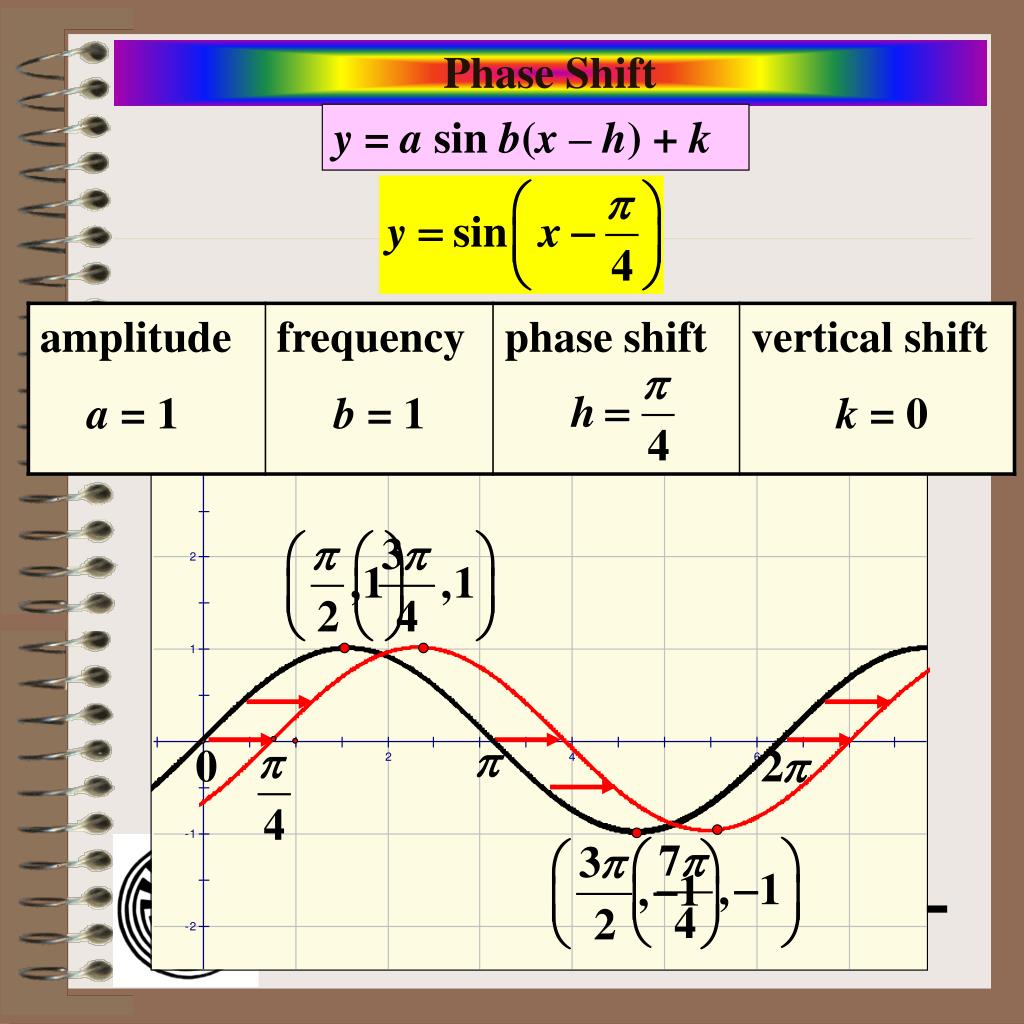
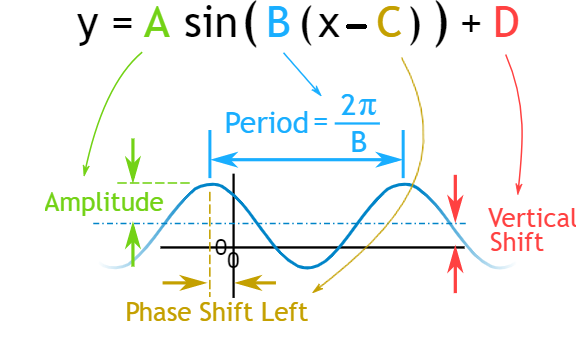
For example, consider the function f(x) = A sin(Bx - φ). Here, A represents the amplitude, B affects the period, and φ is the phase shift.
Understanding the Equation
The equation f(x) = A sin(Bx - φ) encapsulates the key properties of a sinusoidal function. The amplitude, A, determines the height of the wave.
B influences the period; a larger B compresses the wave, making the period shorter. The phase shift, φ, moves the entire wave left or right along the x-axis.
A positive φ shifts the wave to the right, while a negative φ shifts it to the left. The amount of the shift is given by φ/B.
The Significance of Phase Shift
The concept of phase shift might seem abstract, but it has practical implications in numerous fields.
Let's explore a few key applications.
Physics: Waves and Interference
In physics, understanding phase shift is essential for analyzing wave interference. When two waves meet, they can either reinforce each other (constructive interference) or cancel each other out (destructive interference), depending on their relative phases.
If two waves are perfectly in phase (φ = 0), their amplitudes add together. If they are completely out of phase (φ = π), they can cancel each other out completely.
This principle is used in noise-canceling headphones, where the device generates a sound wave that is 180 degrees out of phase with the ambient noise, effectively silencing it.
Electrical Engineering: AC Circuits
In electrical engineering, phase shift plays a critical role in analyzing alternating current (AC) circuits. In an AC circuit containing both inductors and capacitors, the voltage and current are often out of phase.
The phase shift between voltage and current affects the power factor of the circuit, which is a measure of how efficiently electrical power is being used.
Engineers carefully design circuits to minimize phase shift and improve the power factor, leading to more efficient energy usage.
Music: Sound and Harmony
Even in music, phase shift has a subtle but important role. When two instruments play the same note with slightly different timbres, the resulting sound can be richer and more complex.
This complexity arises from the interference of the sound waves produced by the instruments, where slight phase shifts between the waves contribute to the overall sonic texture.
Furthermore, certain audio effects, such as phasing and flanging, intentionally manipulate phase shift to create swirling, ethereal sounds.
Telecommunications: Signal Processing
In telecommunications, phase shift is crucial for encoding and decoding signals. Modulating the phase of a carrier wave allows for the transmission of information.
This technique, known as phase-shift keying (PSK), is widely used in digital communication systems. By varying the phase shift of the carrier wave, different data symbols can be represented.
At the receiving end, the phase shift is detected and used to recover the original data.
Visualizing Phase Shift
To truly grasp the concept of phase shift, it's helpful to visualize it graphically. Imagine a standard sine wave on a graph.
Now, imagine sliding this wave to the left or right. The amount of this slide represents the phase shift.
Software tools like Desmos or Wolfram Alpha allow you to experiment with different values of φ in the equation f(x) = A sin(Bx - φ) and observe how the graph changes in real-time.
Practical Examples
Consider a simple example: f(x) = sin(x) and g(x) = sin(x - π/2). Here, g(x) is simply f(x) shifted to the right by π/2 radians (or 90 degrees).
At x = 0, f(0) = 0, but g(0) = sin(-π/2) = -1. This difference highlights the effect of the phase shift.
Another example could involve two individuals walking in step, but one starts a few paces behind the other. That delay in steps is a real-world representation of phase shift.
Common Misconceptions
One common misconception is that phase shift is the same as time delay. While they are related, they are not identical.
Phase shift is an angular measurement (in radians or degrees), while time delay is a temporal measurement (in seconds or milliseconds). They are related by the period of the function.
Another misconception is that phase shift always represents a delay. A negative phase shift actually represents a lead, meaning the wave starts its cycle earlier than the reference wave.
Conclusion
From the rhythmic sway of ocean waves to the intricate workings of electronic circuits, the concept of phase shift permeates our world. It is more than just a mathematical abstraction; it is a fundamental property that governs the behavior of periodic phenomena.
By understanding phase shift, we gain a deeper appreciation for the intricate interplay of waves and oscillations that shape our reality. It empowers us to predict, analyze, and manipulate these phenomena for a wide range of applications.
So, the next time you hear a complex musical chord, or marvel at the clarity of noise-canceling headphones, remember the subtle dance of waves and the power of phase shift.