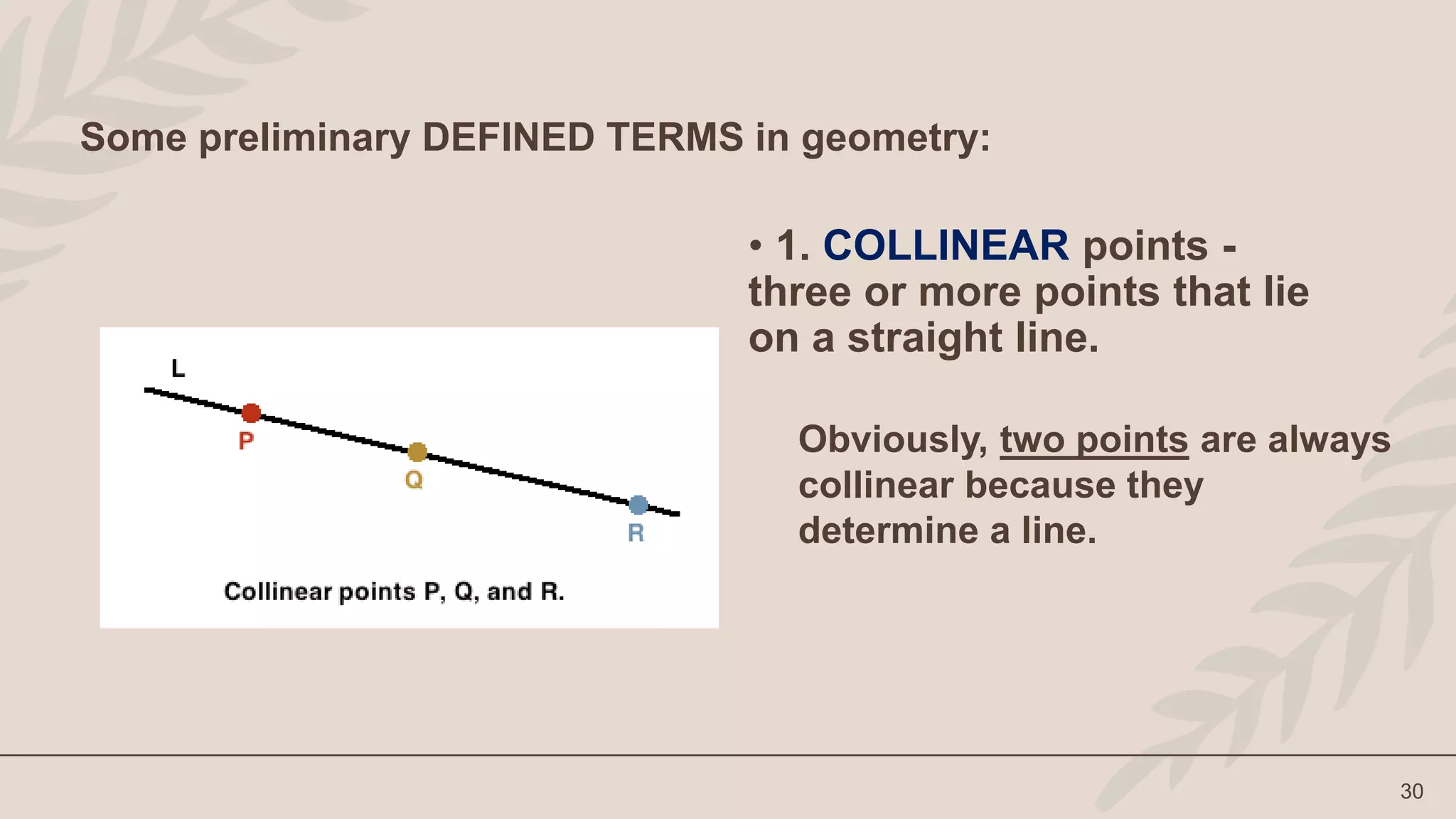
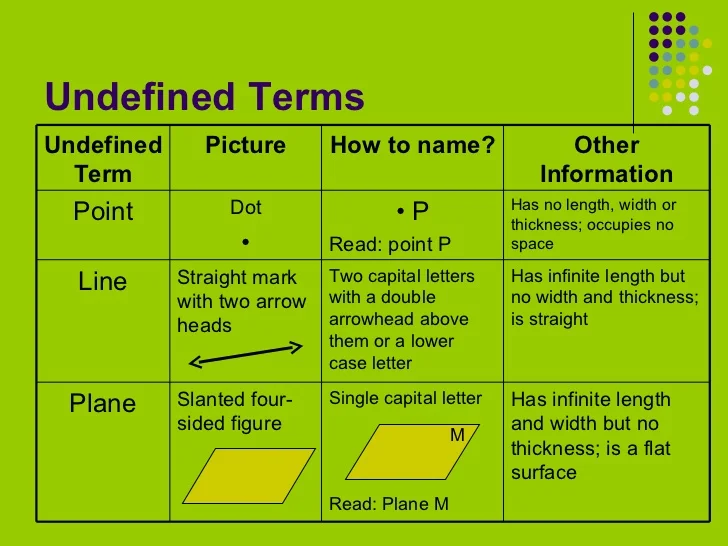
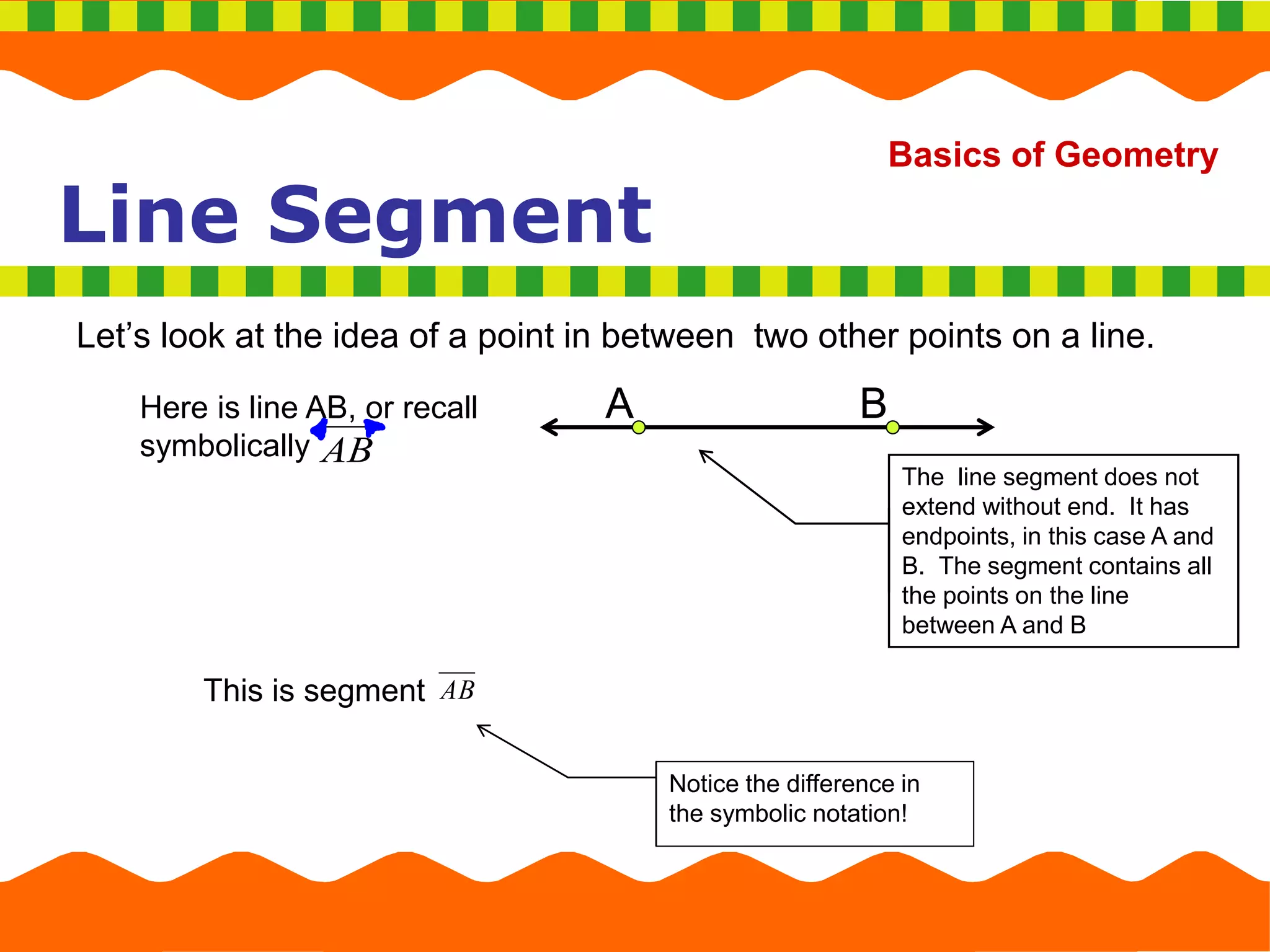
Which Figure Represents An Undefined Term
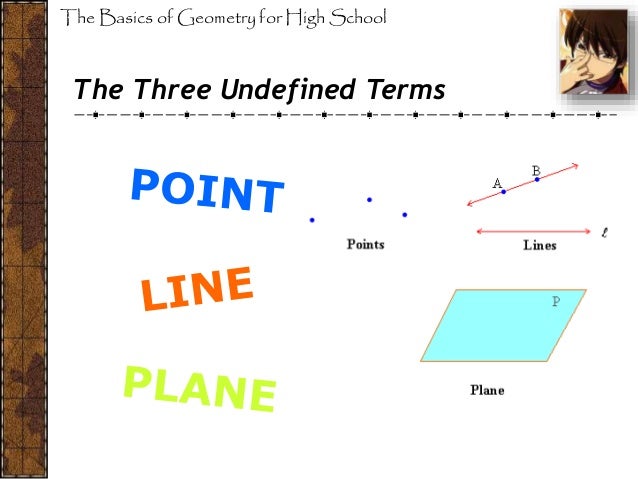
A debate is swirling within the mathematics education community regarding the proper representation of undefined mathematical terms, particularly zero divided by zero and division by zero in general. The discussion, fueled by a recent position paper from the National Council of Teachers of Mathematics (NCTM) and subsequent online discussions, centers around how these concepts are introduced and reinforced in classrooms, and whether current visual and symbolic representations are potentially misleading.
At the heart of the controversy is the lack of a universally accepted, intuitive figure to represent 'undefined'. Critics argue that traditional approaches, often involving crossing out or leaving blank, are not conceptually helpful and may even reinforce misconceptions about the nature of undefined terms. The debate highlights the ongoing effort to improve mathematical literacy and critical thinking skills among students of all ages.
The NCTM Position Paper: A Call for Clarity
The NCTM's position paper, released last month, directly addresses the challenges in teaching undefined terms. It stresses the importance of focusing on the underlying mathematical principles, rather than simply memorizing rules. The paper emphasizes the need for representations that accurately reflect the mathematical properties of limits and the consequences of violating established axioms.
According to Dr. Evelyn Hayes, lead author of the NCTM paper, the issue goes beyond simple notation. "Our goal is to foster a deeper understanding of why division by zero is problematic, and not just dictate that it is forbidden," she stated during a recent webinar. "The representations we use play a crucial role in shaping students' understanding."
Current Representations and Their Shortcomings
Currently, textbooks and educators employ a variety of methods to signify undefined terms. These include: writing "undefined," using the symbol "∅" (empty set, though its meaning is slightly different), leaving the answer blank, or crossing out an equal sign to indicate "not equal to." While these methods communicate the lack of a defined value, critics argue they often fail to explain why the term is undefined.
For example, students may interpret crossing out an answer as a simple error, rather than grasping the fundamental issue of violating mathematical rules. Similarly, simply stating "undefined" without further explanation can lead to rote memorization without true understanding.
The Search for a Better Representation
The quest for a better representation is ongoing. Some educators suggest using graphical representations, such as showing the behavior of a function as it approaches a point where division by zero occurs. This approach can visually demonstrate the concept of a limit and the unbounded nature of the result.
Others advocate for using computer simulations to explore the consequences of attempting to divide by increasingly smaller numbers, highlighting the instability and unpredictable nature of the result. Professor David Lee, a mathematics education researcher at Stanford University, suggests focusing on the properties of the number system itself. "We need to help students understand the axioms that underpin our mathematical system and how division by zero breaks those rules," he said.
"The issue isn't about finding a single perfect symbol," Professor Lee noted. "It's about fostering a conceptual understanding through multiple representations and thoughtful exploration."
Impact on Mathematical Understanding
The way undefined terms are represented has a significant impact on students' overall mathematical understanding. Misconceptions about division by zero, for instance, can hinder progress in algebra, calculus, and other advanced mathematical fields. A deeper understanding of these concepts can lead to improved problem-solving skills and a more nuanced appreciation for the logical structure of mathematics.
Furthermore, clarity in representing undefined terms can contribute to improved mathematical communication. Students who understand the underlying principles are better equipped to explain their reasoning and justify their solutions. This enhanced communication is essential for collaboration and critical thinking in mathematics.
A Broader Discussion About Mathematical Rigor
The debate over undefined terms is part of a larger discussion about mathematical rigor and conceptual understanding. There is a growing consensus among educators that rote memorization is insufficient for developing true mathematical competence. Instead, students need opportunities to explore mathematical concepts through hands-on activities, discussions, and problem-solving.
The focus is shifting towards helping students develop a deeper understanding of the why behind the mathematics, rather than simply the how. This requires a fundamental change in teaching practices and the development of new resources that support conceptual understanding.
Ultimately, the search for a better representation of undefined terms reflects a commitment to improving mathematics education and fostering a generation of critical thinkers. While a single, universally accepted solution may not emerge, the ongoing dialogue and exploration will undoubtedly lead to more effective teaching practices and a deeper understanding of mathematics for all students.
