Which Of The Following Is Not A Continuous Variable

A critical misunderstanding of statistical concepts is sweeping through data analysis fields, threatening the validity of research findings. Identifying discrete versus continuous variables is paramount, and a failure to do so leads to flawed conclusions.

The question of whether a variable is continuous is fundamental to data analysis. Errors in variable classification undermine statistical tests and can lead to disastrous misinterpretations across various sectors, from healthcare to finance.

Understanding Variable Types

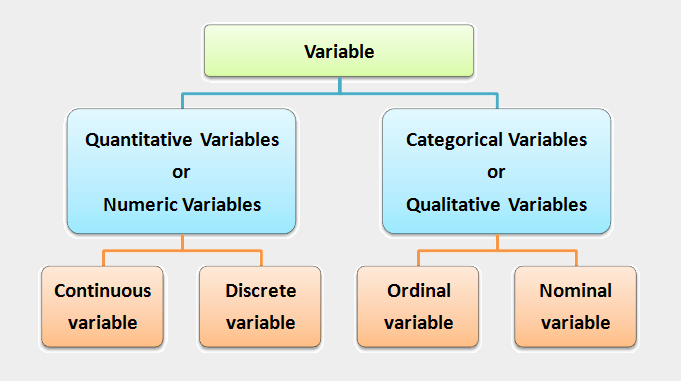
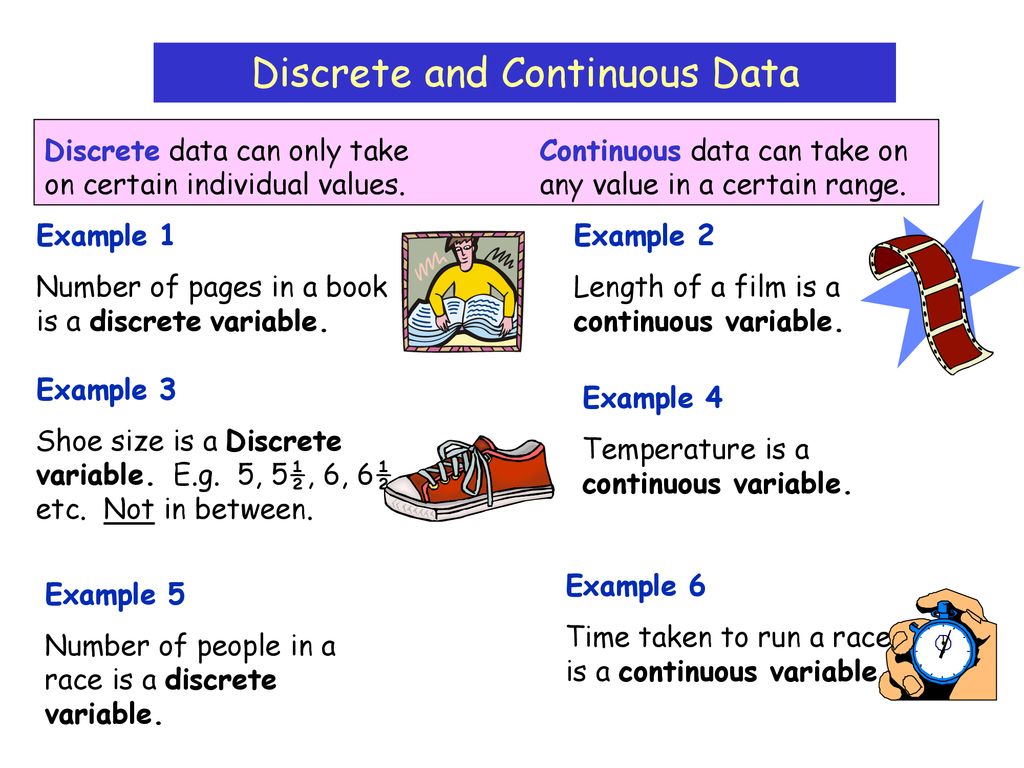
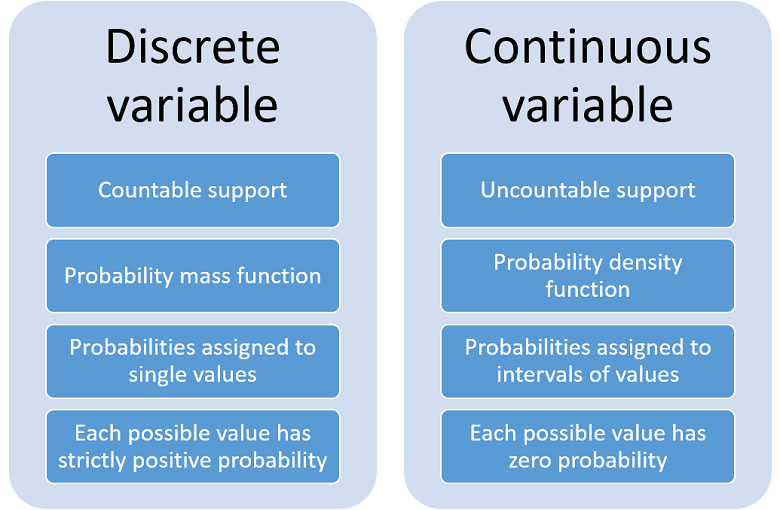
Variables are broadly categorized into two types: discrete and continuous. Discrete variables are countable and can only take on specific, separate values. Think of the number of students in a class or the number of cars passing a point on a highway in an hour.

Continuous variables, on the other hand, can take on any value within a given range. Examples include height, temperature, and time.

The Critical Distinction

The distinction lies in the potential for intermediate values. A continuous variable can, theoretically, be measured with infinite precision between any two given points.

A discrete variable cannot. It jumps between distinct values.

The Peril of Misclassification

Misclassifying a variable has serious consequences. Using statistical methods designed for continuous variables on discrete data (or vice versa) invalidates the results.

This can lead to incorrect inferences and poor decision-making. Imagine using a continuous variable test on the number of customer complaints—the results would be statistically meaningless.

Common Examples and Pitfalls

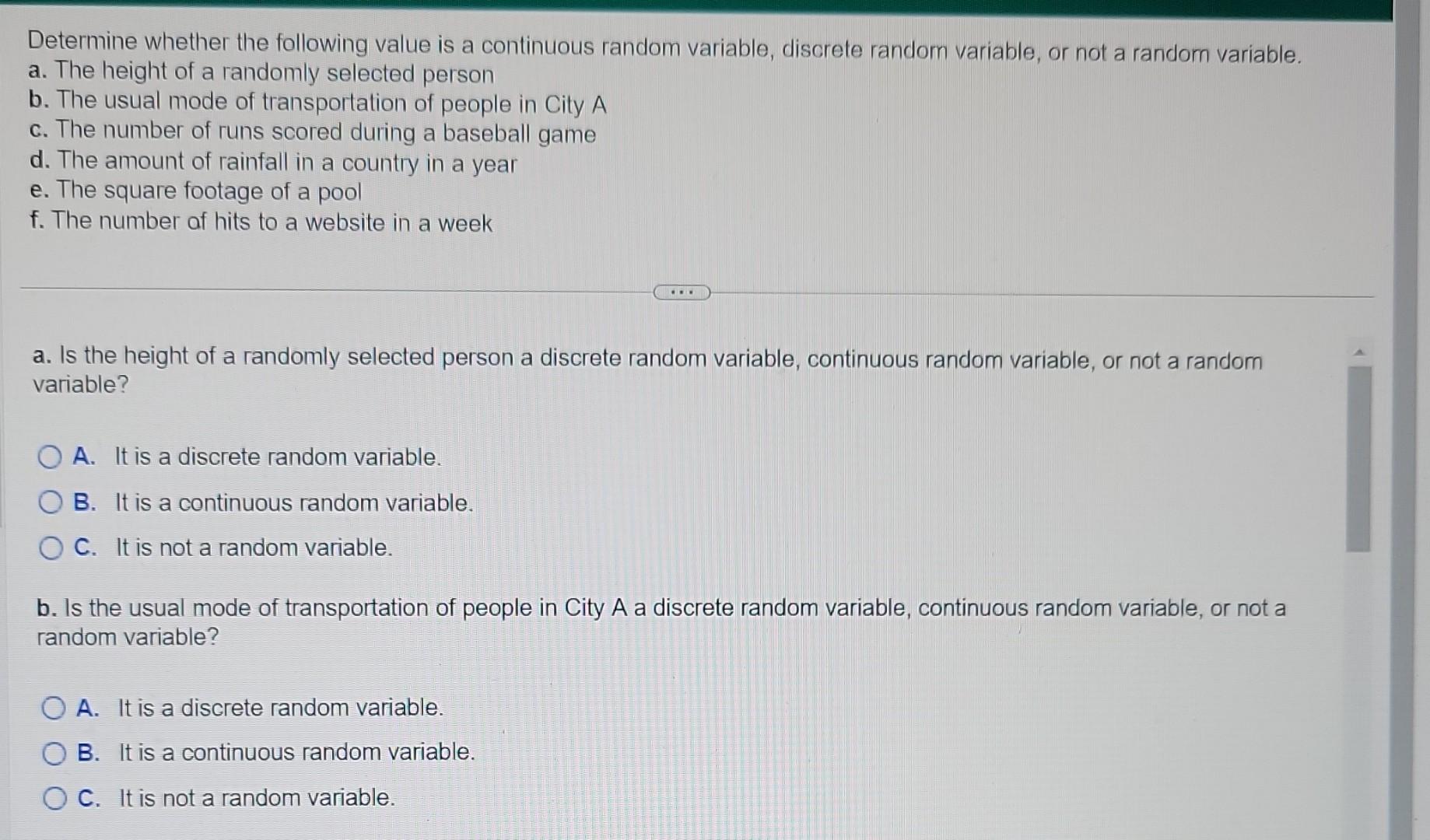
One frequently cited example is age. While often treated as continuous, age reported in whole years is, technically, discrete.

However, for many analyses, the approximation of treating it as continuous is acceptable, especially with large datasets. This is where the analyst's judgment becomes crucial.

The key is understanding the underlying nature of the data and the potential impact of the approximation.

Illustrative Cases

Consider these examples: Number of siblings: Discrete. Weight: Continuous. Number of houses in a neighborhood: Discrete.

Temperature in Celsius: Continuous. Ratings on a 1-5 scale: Discrete (though often treated as continuous with caution).

These examples highlight the importance of critical thinking when classifying variables.

The Importance of Measurement Scale

The measurement scale also plays a crucial role. Variables can be nominal, ordinal, interval, or ratio.

Nominal variables (e.g., colors) are categorical and unordered. Ordinal variables (e.g., satisfaction ratings) have a meaningful order but unequal intervals. Interval variables (e.g., temperature in Celsius) have equal intervals but no true zero point.

Ratio variables (e.g., height) have equal intervals and a true zero point.

Addressing the Knowledge Gap

Several educational resources are being developed to address this widespread misunderstanding. Online tutorials, workshops, and revised statistical curricula are underway.

These initiatives aim to equip data analysts with the necessary skills to accurately classify variables and apply appropriate statistical methods. This is not merely an academic exercise; it directly impacts the reliability and validity of research.

Universities and professional organizations are stepping up to provide training. The goal is to enhance data literacy and reduce errors in statistical analysis.

Expert Opinions

“A solid understanding of variable types is the bedrock of sound statistical practice,” says Dr. Anya Sharma, a professor of statistics at the University of California, Berkeley. “Neglecting this foundation can lead to misleading conclusions and flawed decision-making.”

Dr. Ben Carter, a data scientist at Google, emphasized the practical implications. “In the real world, misclassification can have significant financial and ethical consequences. We must prioritize training and education in this area.”

Their views underscore the pressing need for action.

Ongoing Developments

Research into automated variable classification techniques is ongoing. While these tools can assist in the process, they are not a replacement for human judgment.

The analyst must always understand the context of the data and critically evaluate the results. Technology should augment, not replace, human expertise.

Further studies are needed to quantify the extent of misclassification errors and their impact on various fields.