Which Of The Following Statements Is A Proposition

Confusion and misinformation are spreading rapidly online regarding a seemingly simple question: "Which of the Following Statements Is a Proposition?". The debate hinges on understanding fundamental logical principles and has sparked heated discussions across educational platforms and social media.
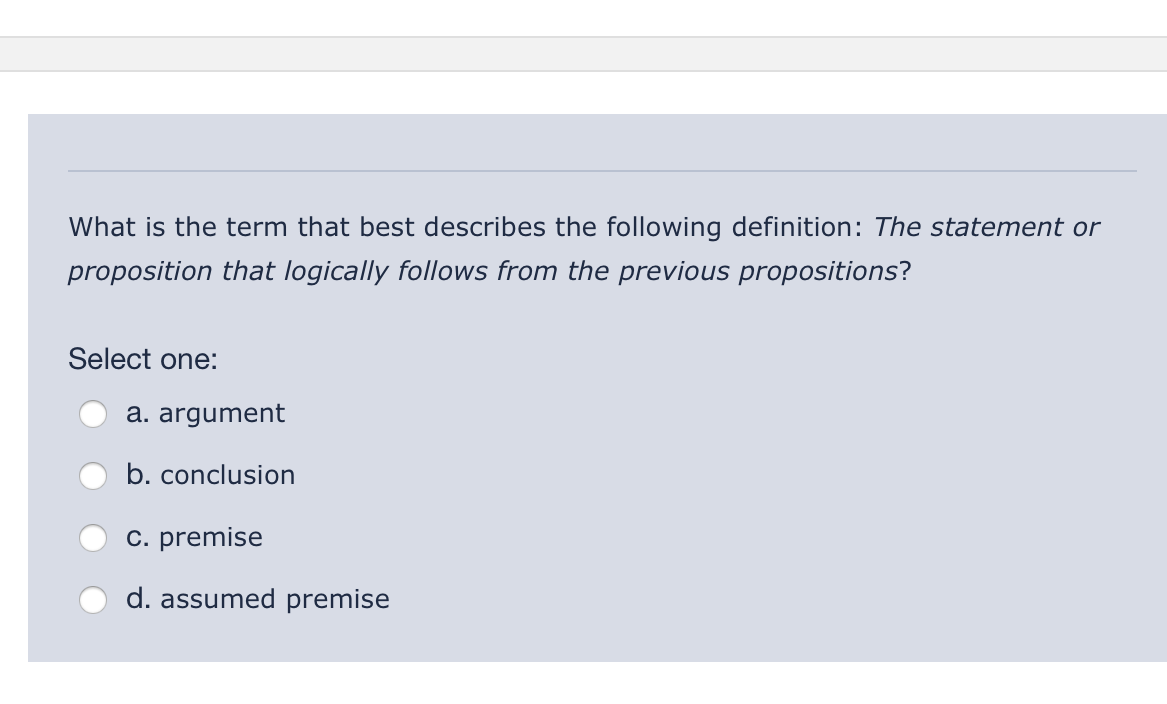
The core issue revolves around defining what constitutes a proposition in logic – a statement that can be either true or false, but not both. The correct identification of propositions is crucial for valid reasoning and critical thinking, yet the concept is frequently misunderstood, leading to widespread errors in analysis and argumentation.
Defining a Proposition: The Basics
In logic, a proposition, also known as a statement, is a declarative sentence that asserts something. Crucially, a proposition must have a truth value, meaning it can be definitively classified as either true or false.
Questions, commands, exclamations, and opinions are generally not considered propositions because they do not assert a fact that can be verified as true or false. For example, "Close the door!" is a command and cannot be assigned a truth value.
Common Misconceptions
Many individuals struggle to differentiate between statements of fact and subjective opinions. "Chocolate ice cream is delicious" is an opinion and not a proposition, as its truth value depends on individual preferences.
Similarly, rhetorical questions, while phrased as questions, often function as assertions. However, in a strict logical sense, they are still technically questions and not propositions.
Examples and Analysis
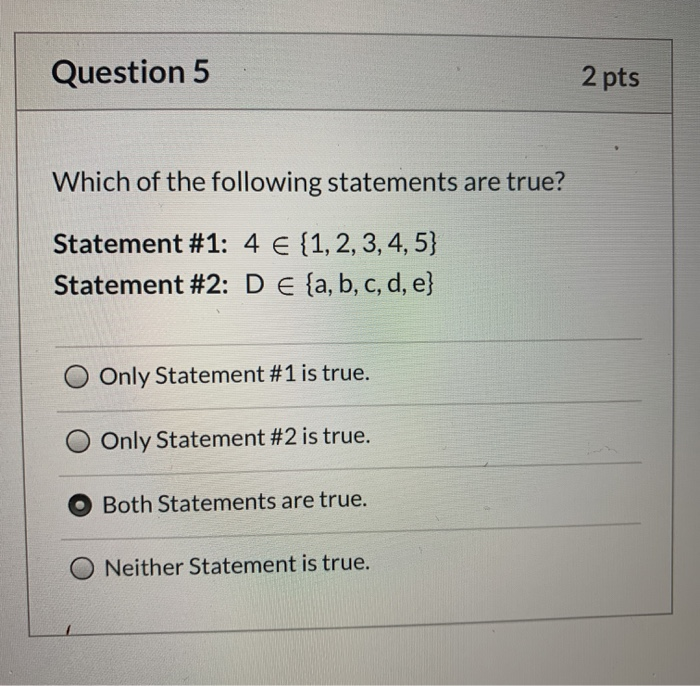
Consider these examples: "The Earth is flat," and "2 + 2 = 4." The first is a proposition, albeit a false one. The second is a proposition, and a true one.
Contrast these with "What time is it?" and "Ouch!". Neither of these can be assigned a truth value, therefore they are not propositions.
A statement like "This sentence is false" presents a special case known as a paradox. While it seems like a proposition, it leads to a logical contradiction and is generally excluded from the realm of valid propositions in formal logic.
Why This Matters
The ability to identify propositions is fundamental to constructing valid arguments and avoiding logical fallacies. In fields ranging from mathematics and computer science to law and philosophy, precise reasoning is paramount.
Misunderstanding propositions can lead to flawed conclusions and ineffective communication. Critical thinking skills, therefore, heavily rely on this basic logical concept.
The current online debate highlights a deficiency in logical literacy. Many users incorrectly identify statements based on personal beliefs or emotional reactions, rather than adhering to the objective criteria of truth value.
Addressing the Confusion
Educational institutions and online learning platforms are urged to emphasize the principles of logic more effectively. Clear explanations and practical examples are crucial for reinforcing understanding.
Resources like online logic courses, textbooks, and interactive exercises can help individuals develop their ability to identify propositions accurately. Self-assessment and practice are key to mastery.
Collaboration between educators and content creators is needed to disseminate accurate information and debunk common misconceptions. Simple, accessible explanations can reach a wider audience and promote logical reasoning.
Next Steps
Efforts are underway to create freely available online resources dedicated to explaining propositional logic. These resources will include interactive quizzes, video tutorials, and detailed explanations.
A coalition of educators and logicians are planning a series of webinars and workshops aimed at improving logical literacy among students and the general public. The first webinar is scheduled for next month.
The ongoing discussion about propositions underscores the importance of continuous learning and critical evaluation of information. As misinformation continues to spread, logical reasoning remains a vital tool for navigating the complexities of the modern world.