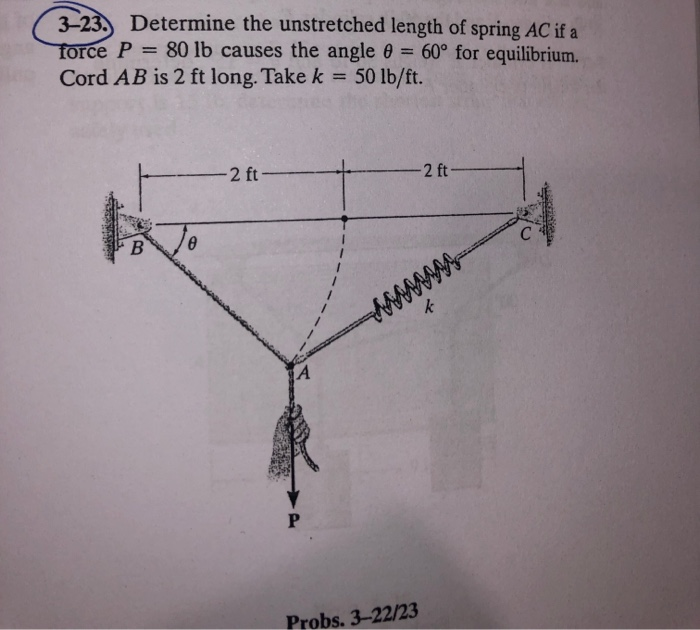
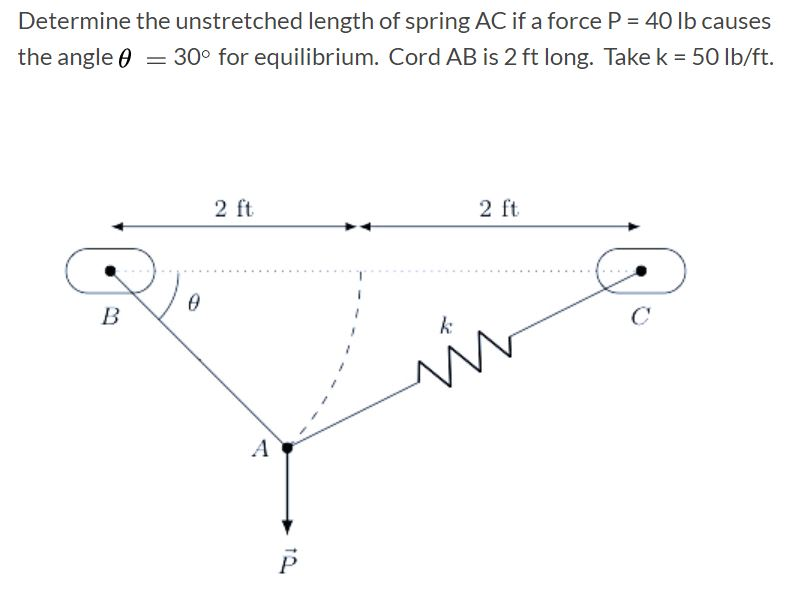
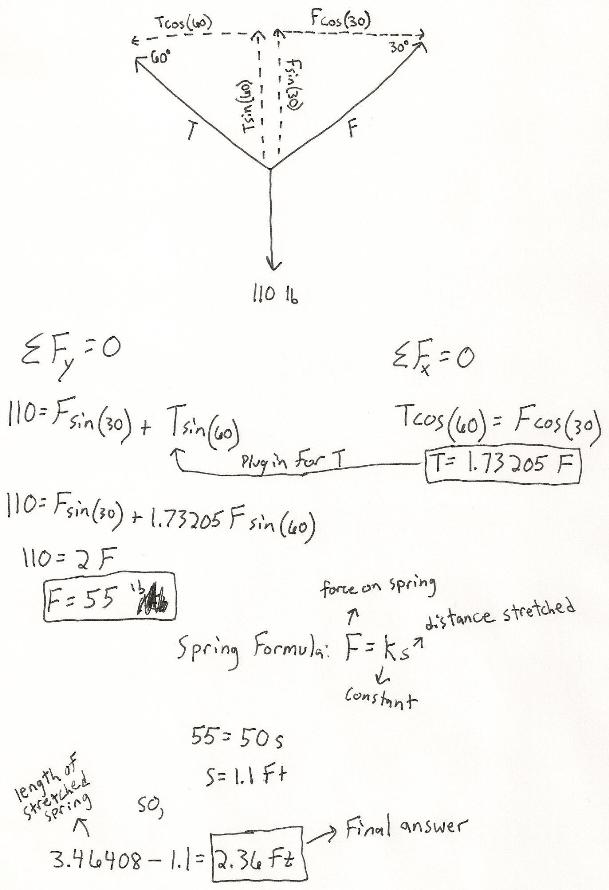
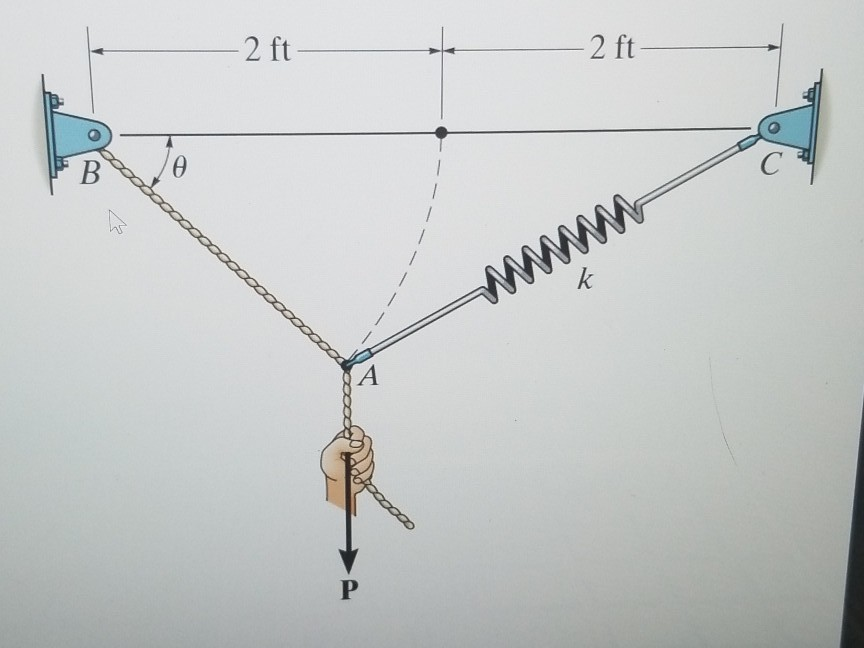
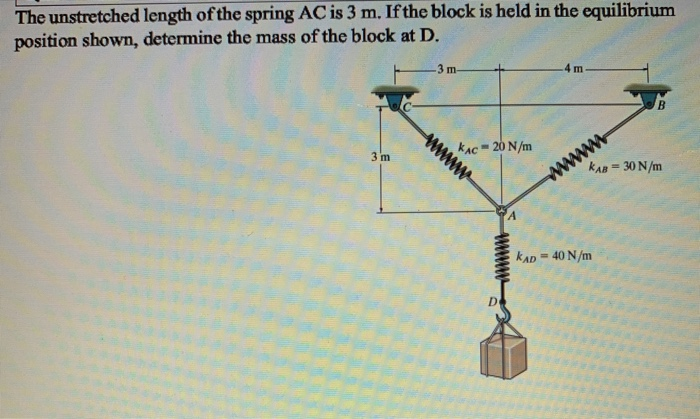
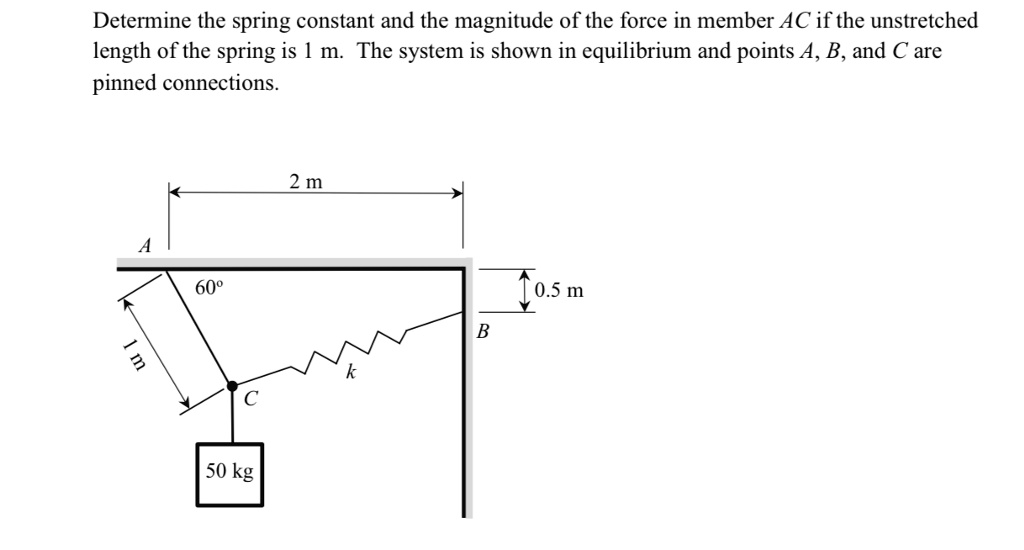
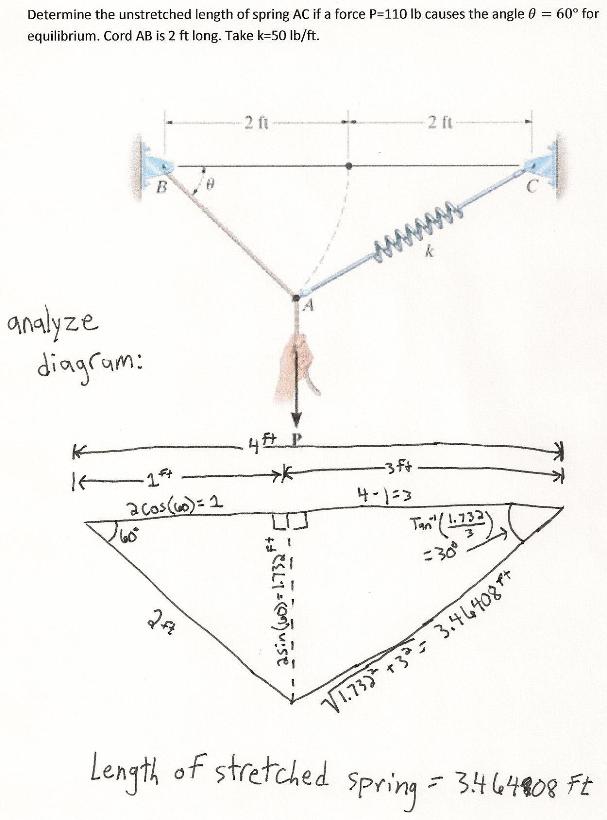
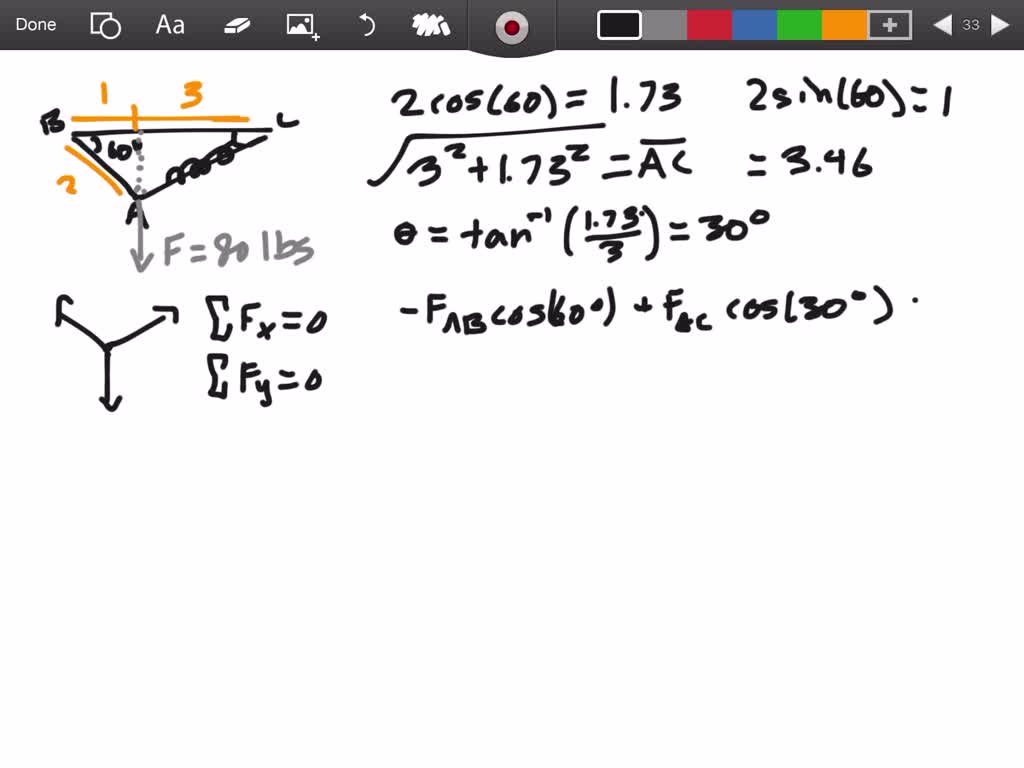
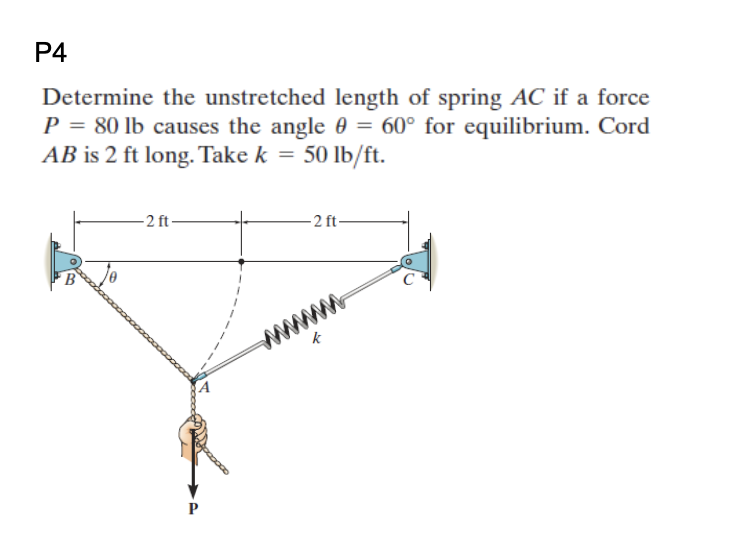
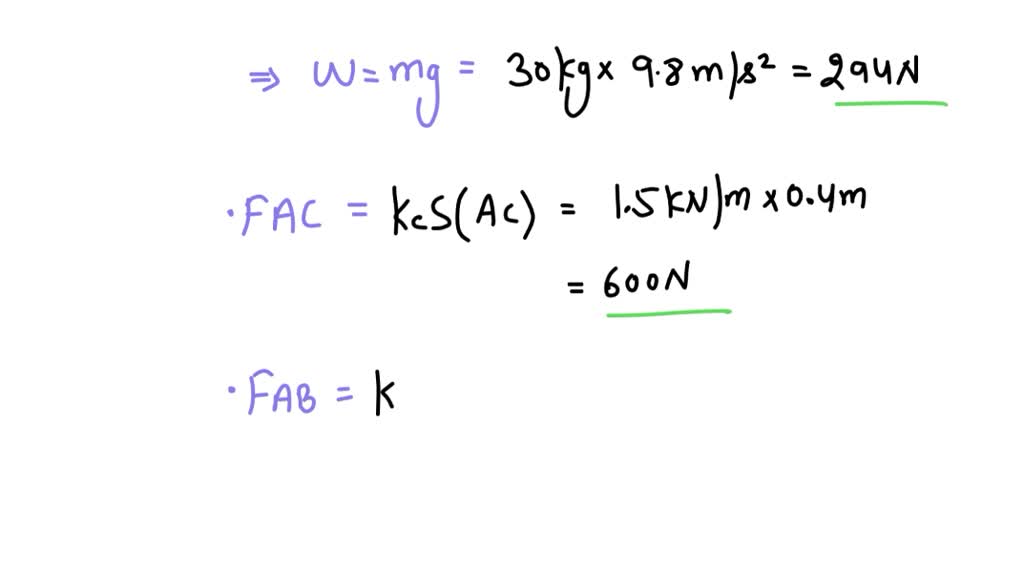Determine The Unstretched Length Of Spring Ac

Ever stretched a Slinky way too far? We've all been there! Figuring out the original length of a spring before you put it to work (or, you know, accidentally turn it into a wobbly noodle) is simpler than you think. Think of it as detective work for bouncy things!

The Core Concept: It's All About the Stretch

The magic behind finding the unstretched length lies in understanding how springs behave. They follow a pretty predictable pattern when you pull on them. This predictability is our secret weapon!

Imagine you're stretching a rubber band. The further you stretch it, the harder you have to pull, right? That's kind of what we're banking on.

What We Need

To solve this springy mystery, we need a few key pieces of information. It's like gathering clues at a crime scene, but instead of a magnifying glass, we're using a ruler and our brainpower!

First, we need at least two sets of data: the force applied to the spring and the resulting length of the spring. Think of it as knowing how hard you pulled and how far the spring stretched.

Second, we need to assume the spring is linear. No twisty or crazy springs please.

Let's Get Practical

Let's say you hung a 1 kg weight on a spring, and it stretched to 12 cm. Then, you hung a 2 kg weight, and it stretched to 17 cm. We're in business! Okay, let's turn these into force units.

1 kg equals roughly 9.8 Newtons (N) of force. Similarly, 2 kg equals roughly 19.6 Newtons of force.

We have our data now. When you apply 9.8 N force, the spring length is 12 cm. Similarly, when you apply 19.6 N force, the spring length is 17 cm.

The Magic Formula (Kind Of)

Now for the big reveal! We need a formula that relates force, spring length, and the spring constant (how stiff the spring is). That formula is: F = k * (L - L0), where F is the force, k is the spring constant, L is the stretched length, and L0 is the unstretched length (what we're after!).

Since we have two sets of data, we can setup a system of two equations with two unknowns (k and L0): 9.8 = k * (12 - L0) and 19.6 = k * (17 - L0).

Solving these equation is a bit of algebra gymnastics. You can use substitution method. Solve for k in one equation: k = 9.8 / (12 - L0). Plug it into the other equation, 19.6 = (9.8 / (12 - L0)) * (17 - L0).

After simplifying, you can get 2 * (12 - L0) = 17 - L0. Expand the equation: 24 - 2L0 = 17 - L0. Re-arrange the equation: L0 = 7.

Ta-da! The unstretched length of the spring is approximately 7 cm. We did it!

Important Caveats (Because Physics Isn't Always Perfect)

This method assumes the spring behaves perfectly linearly, which isn't always the case in real life. Some springs become non-linear at large stretched. It's a bit like assuming your friend will always share their pizza crusts – sometimes they just won't!

Also, make sure you don't stretch the spring beyond its elastic limit, because that'll permanently damage the spring. That's like trying to fold a piece of paper more than seven times – it's just not going to happen without some serious damage!

If the spring is very weak, the gravity might be a problem. You need to take into account the initial position of the spring.

Conclusion

Finding the unstretched length of a spring is a fun little puzzle with real-world applications. So go forth, measure some springs, and impress your friends with your newfound physics prowess!

And remember, a little bit of detective work can go a long way, especially when it comes to understanding the bouncy world around us.