Express In Terms Of Sums And Differences Of Logarithms
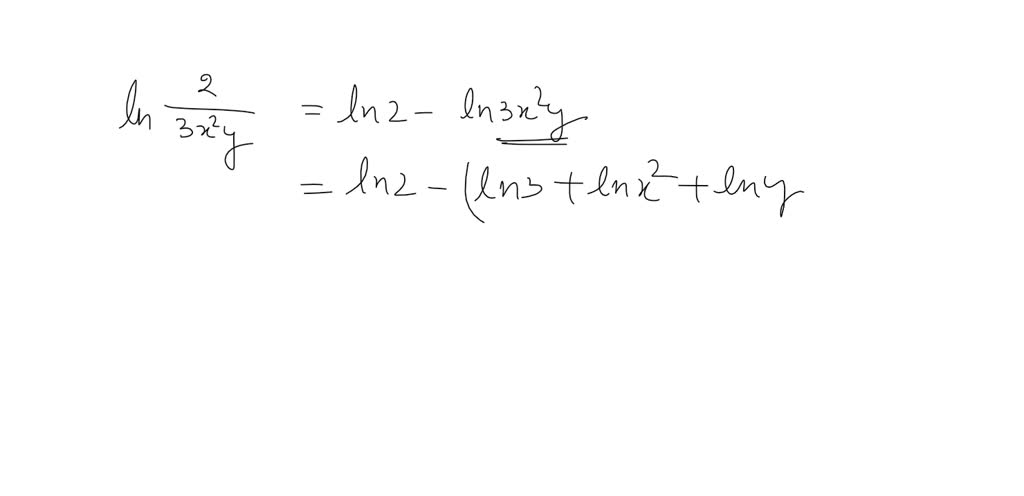
Ever feel like math is a tangled mess? Like untangling Christmas lights... only with numbers? Well, get ready for a neat trick that's surprisingly satisfying.
It’s all about playing with logarithms! And not just any playing. We're talking about turning multiplication and division problems into simpler addition and subtraction ones.
The Logarithm Lowdown (Made Easy!)
Think of logarithms as secret code unlockers. They help us simplify complex calculations.
Suddenly, huge numbers seem manageable. It's like having a superpower for math!
We’re basically taking these log expressions and breaking them down. We rewrite them as additions and subtractions of other logs. Cool, right?
Why Is This So Fun?
Okay, "fun" might be a strong word for some. But trust us, there's a certain satisfaction to this.
Imagine you have a really complicated expression. It's a logjam of numbers and operations!
Then, with a few clever moves, you transform it into something clean and organized. Think of it like decluttering your desk, or finally understanding that weird dream you had.
It's like a mathematical puzzle where the solution is elegant simplicity. You started with a hairy beast, but finished with a sleek, well-groomed kitten. Purrfect!
The Secret Ingredients: Log Rules
There are a few key rules, but they are super intuitive. They’re the secret sauce!
One rule says that multiplying inside a log is like adding the logs separately. Log(A*B) becomes Log(A) + Log(B).
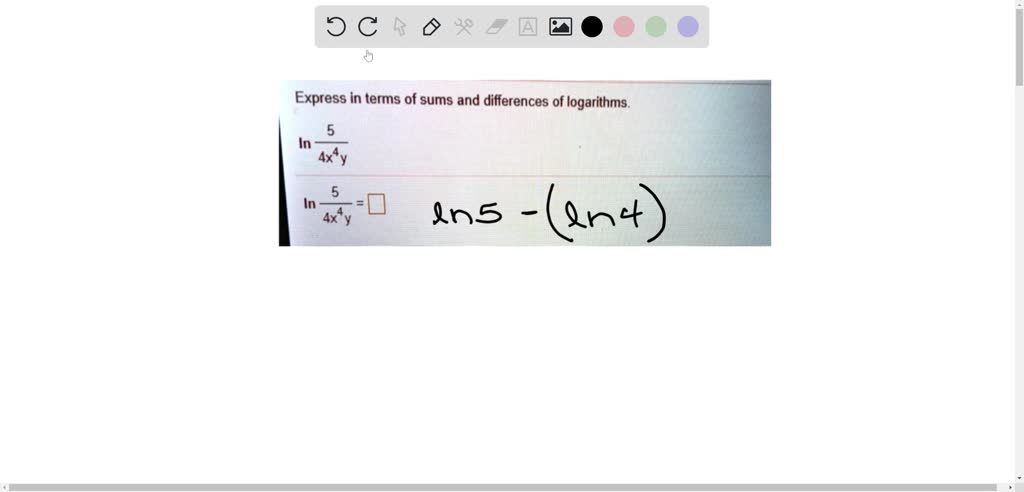
Another says dividing inside a log is like subtracting the logs. Log(A/B) becomes Log(A) - Log(B). It’s like magic!
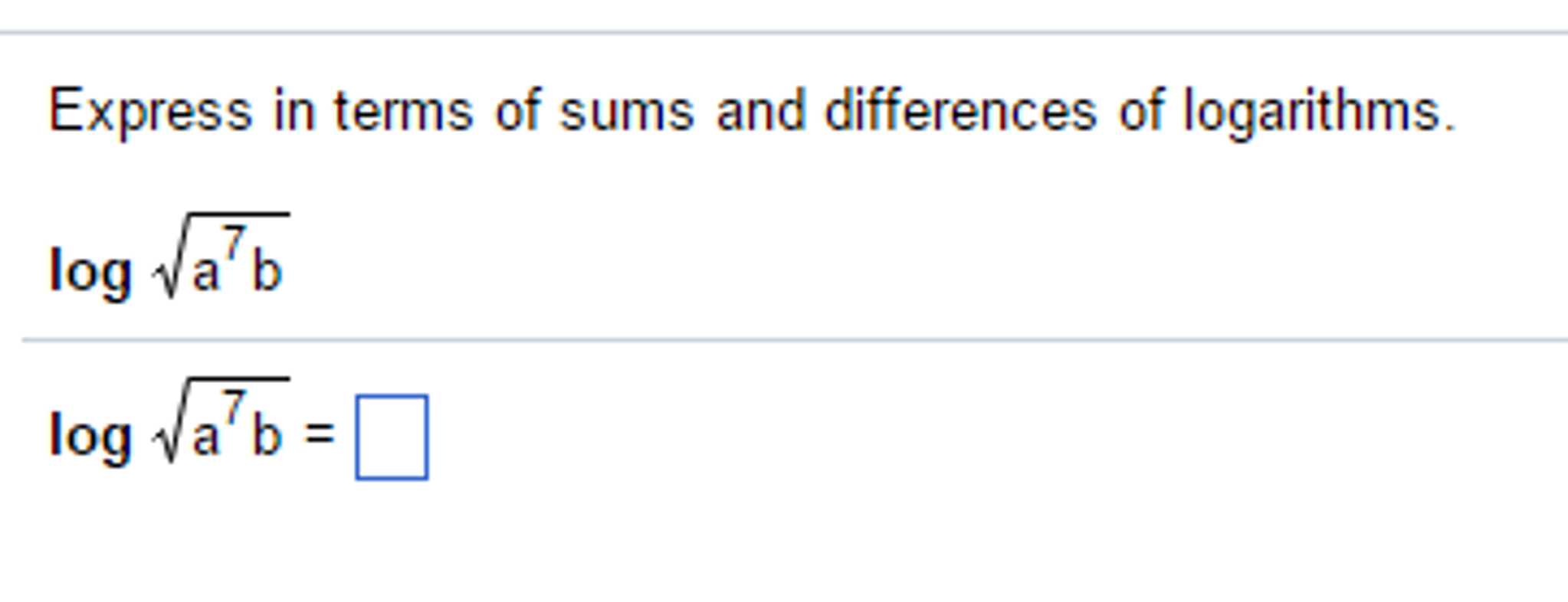
What about powers? Log(AB) becomes B * Log(A). The exponent becomes a multiplier!
These rules are the keys to the kingdom. Master them, and you can conquer any logarithmic expression.
Example Time!
Let’s say we have log(x*y/z). Using the rules above, we can rewrite this as log(x) + log(y) - log(z).
See how we turned multiplication into addition and division into subtraction? Pretty slick, huh?
Let's try a slightly harder one. Suppose we have log( (a2 * b) / c3 ).
Break it down: log(a2) + log(b) - log(c3). Then simplify further: 2log(a) + log(b) - 3log(c).
Beyond the Basics
This skill isn't just about showing off your math prowess. It has real-world applications.
It's used in computer science, engineering, and even finance. Simplifying complex equations is a crucial step in many fields. Mastering logarithmic manipulation helps you see the hidden structure within complex formulas.
Give It a Try!
So, are you ready to dive in? Don't be intimidated. Grab a pencil, some paper, and a few log expressions. Experiment with those rules!
You might be surprised at how quickly you get the hang of it. Plus, the feeling of unlocking those equations is strangely addictive.
Who knows? You might just discover your inner math wizard! It's all about understanding logarithms and their properties. Embrace the challenge and see what wonders you can unfold!
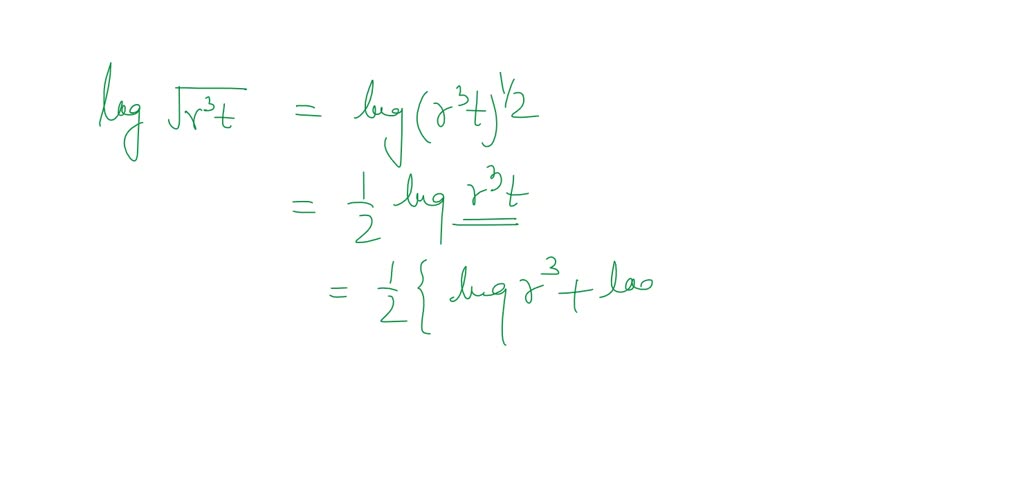


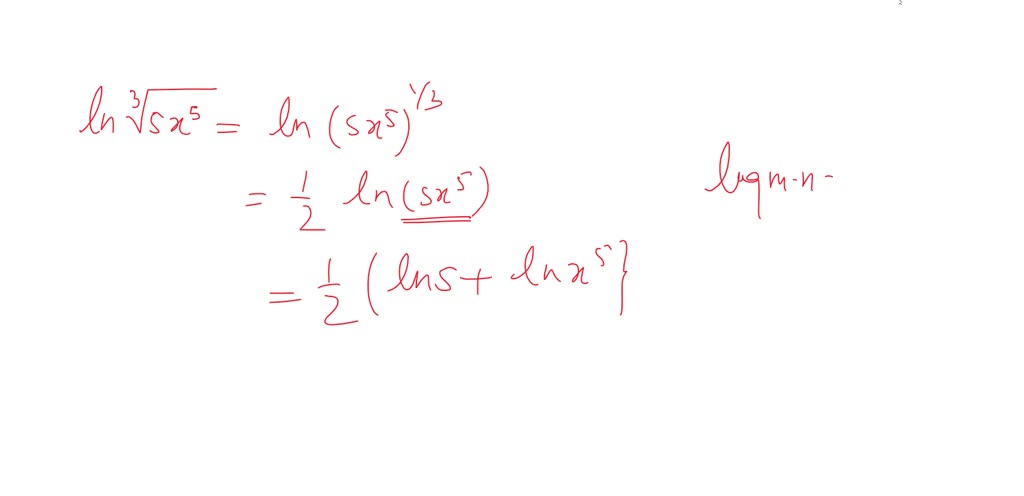

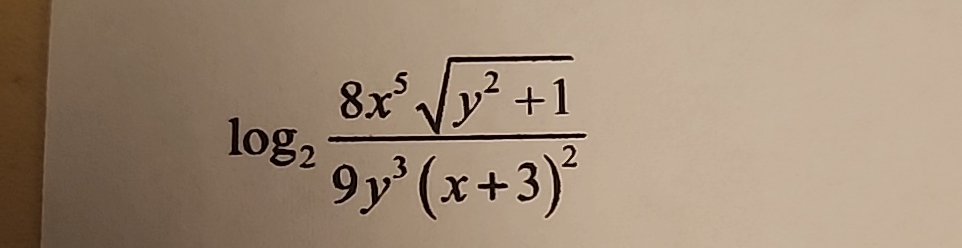
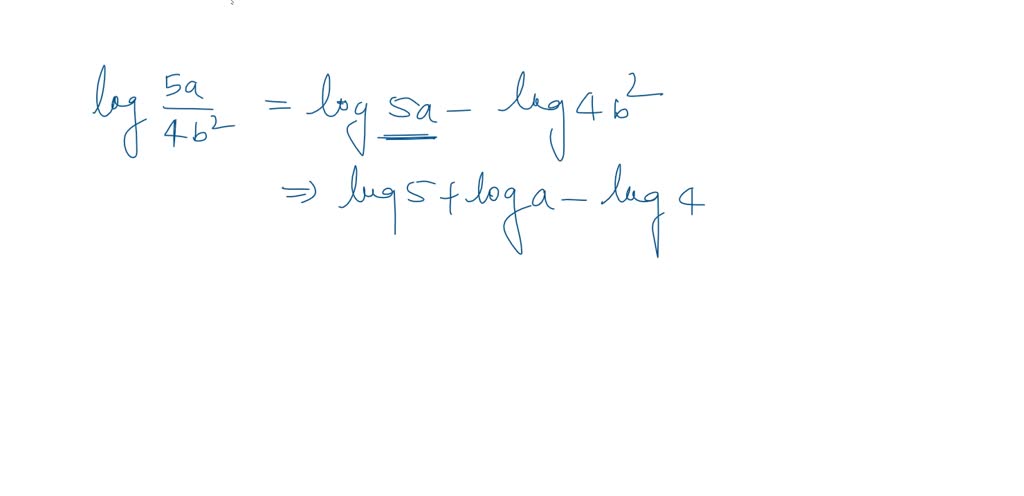





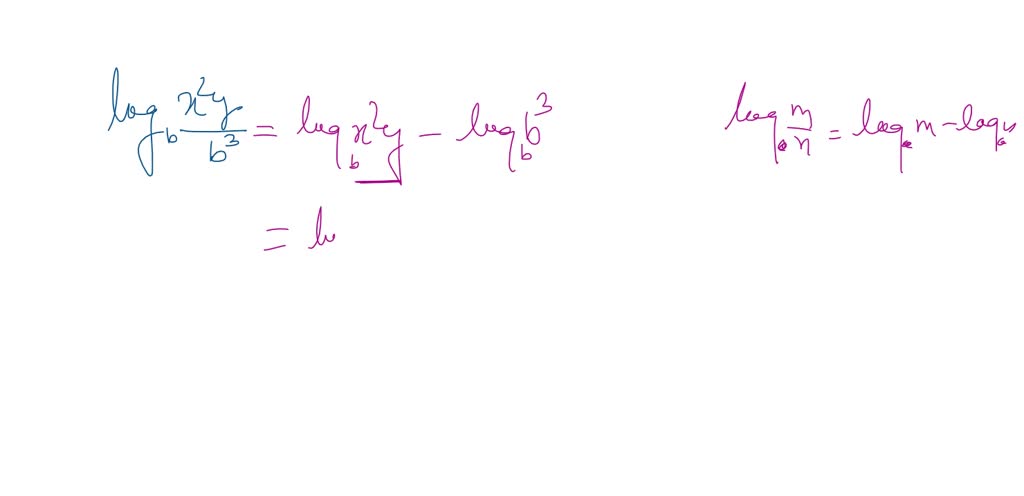
![Express In Terms Of Sums And Differences Of Logarithms [ANSWERED] Express in terms of sums and differences of logarithms log a](https://media.kunduz.com/media/sug-question-candidate/20220701035238259413-4356528.jpg?h=512)
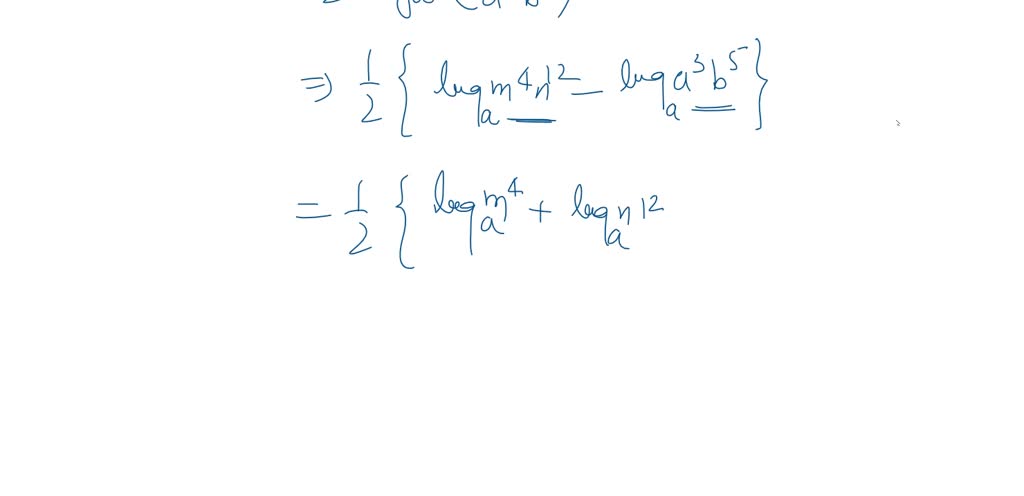
![Express In Terms Of Sums And Differences Of Logarithms [ANSWERED] Express in terms of sums and differences of logarithms In 4](https://media.kunduz.com/media/sug-question-candidate/20230409030015819381-4341414.jpg?h=512)
