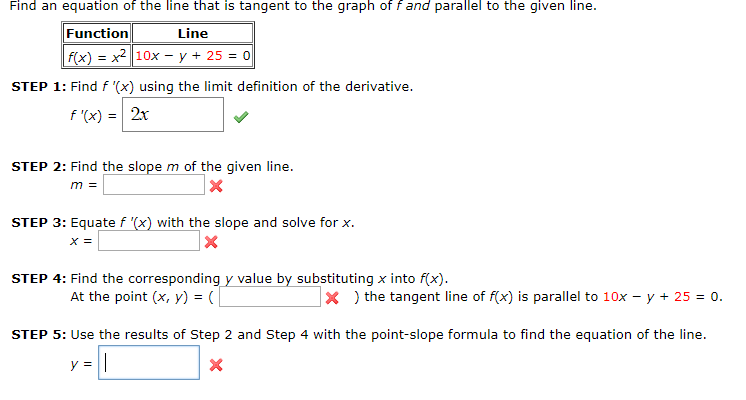
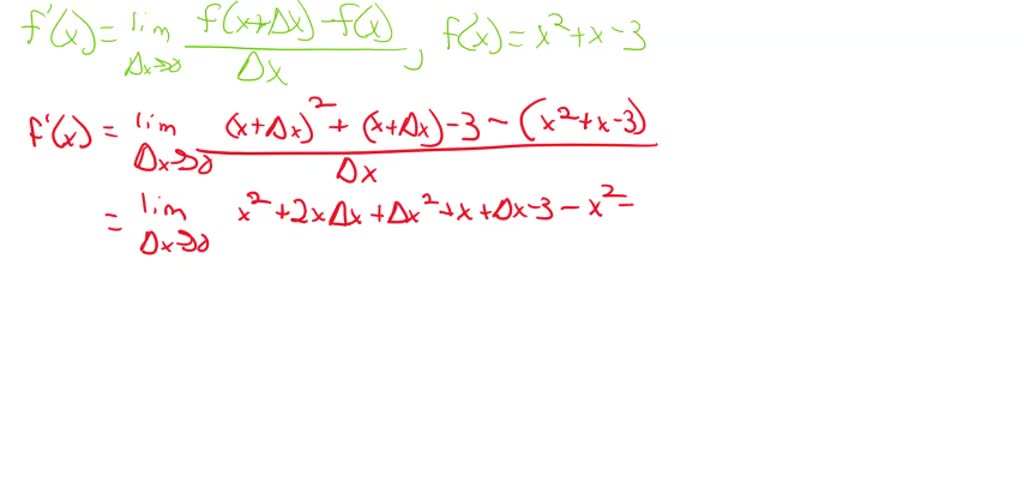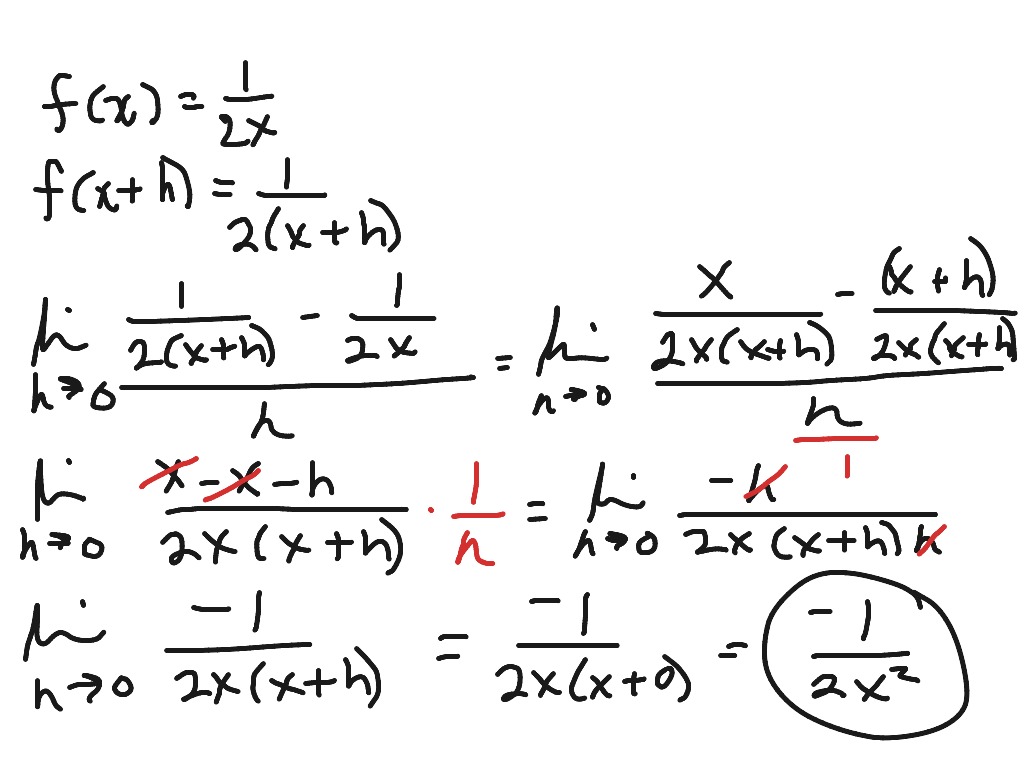Find The Derivative Of The Function By The Limit Process

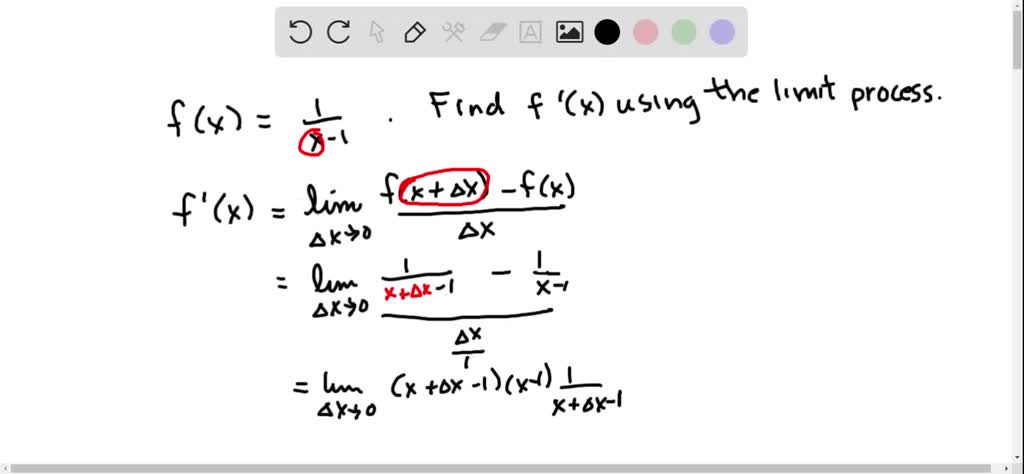
Ever wondered how mathematicians find the speed of something when its speed is constantly changing? It's like trying to catch a greased piglet – slippery and fast!

Well, they use a secret weapon called the limit process to find the derivative. Think of the derivative as the speedometer of a curvy roller coaster track.

The Greased Piglet Analogy

Imagine you're chasing that greased piglet. You get closer and closer, but never quite catch it. That "getting closer and closer" feeling is kind of like what happens with limits.

You're not *exactly* at the point where you want to find the speed, but you're so close it almost doesn't matter. This "almost doesn't matter" is the heart of the limit process.

Zooming In for the Win

Consider a curve drawn in chalk on the sidewalk. Now, put on your magic glasses that let you zoom in, like, a *lot*.

As you zoom in closer and closer to a particular point, that curve starts to look like a straight line. And *bam*! That straight line’s slope is the derivative at that point.

It’s like turning a wild, unpredictable dance into a simple two-step, but only when you're super, super close.

The Infinitesimal Magician

The limit process involves shrinking the distance between two points on the curve to something ridiculously tiny – what mathematicians call an infinitesimal change.

Think of it as using a microscope to analyze the smallest possible step a ladybug takes on a leaf.

This infinitesimal step helps us calculate the slope, which is the derivative, which gives us the instantaneous speed. It’s like having a built-in speedometer for the ladybug.

The Formula Fumble (But Don't Panic!)

Okay, there's a formula involved, but don’t let that scare you! It looks something like this: lim (h -> 0) [f(x+h) - f(x)] / h.

This is the formal way to describe the "getting closer and closer" idea. It's essentially figuring out the slope of the line when the distance `h` between the points is almost zero. Think of h as the distance between you and the greased piglet.

Don't worry about memorizing it right now! The important thing is to understand the *idea* behind it.

From Mystery to Mastery (Maybe!)

The limit process might seem intimidating at first. But with a little practice, it becomes a powerful tool.

It reveals the hidden speed secrets within those curvy functions, like uncovering the secret ingredient in your grandma's famous cookies.

So next time you see a derivative, don't be afraid! Remember the greased piglet, the zooming glasses, and the infinitesimal ladybug steps. Think of Isaac Newton and Gottfried Wilhelm Leibniz, the dynamic duo who basically invented this stuff.

And remember, even mathematicians sometimes chase slippery concepts!