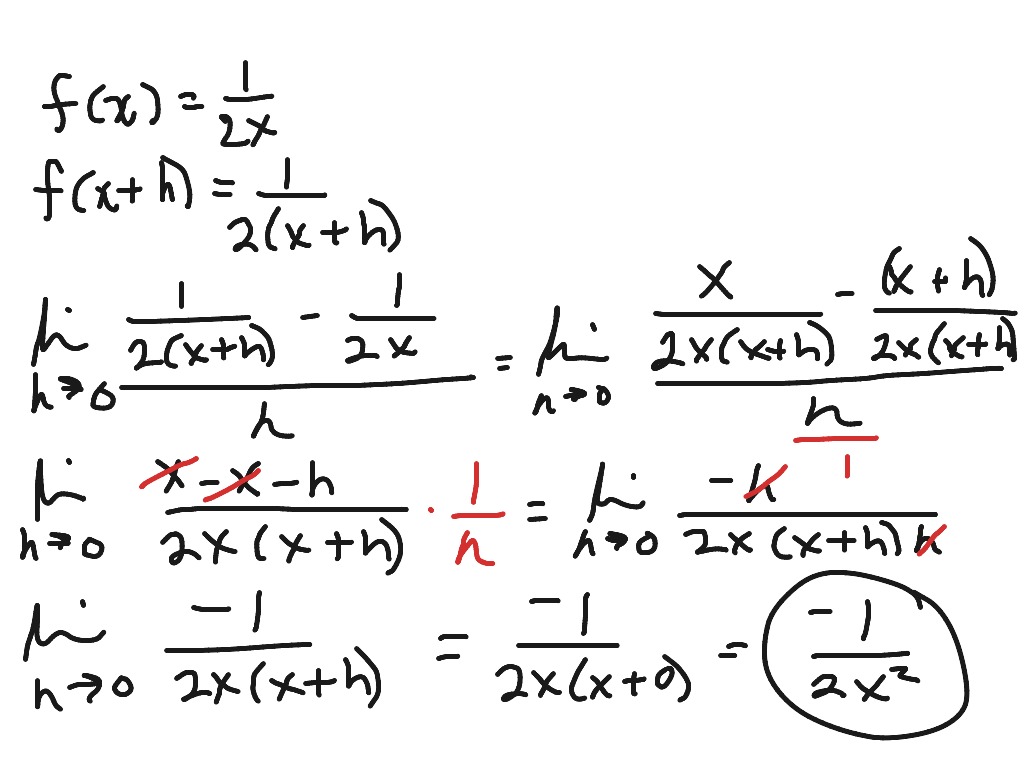How To Find The Derivative Using The Limit Process

Alright, buckle up buttercups! We're diving into the world of derivatives using something called the *limit process*! Don't let the fancy name scare you; it's actually quite a groovy dance!

The "Rise Over Run" Refrain

Imagine you're chilling on a super-fun roller coaster. You want to know exactly how steep the track is at a particular point.

That's where the idea of *slope*, or "rise over run," comes in handy. Remember that old friend from algebra class?

We just need two points on the line to do this. But the challenge here is that we want to know the slope at a *single point*!

Zooming In Like a Math Detective

Here's where our secret weapon, the *limit process*, comes into play! We pick a second point *really, really* close to our point of interest.

Like, microscopically close! So close, they're practically twins sharing a pizza!

We calculate the slope between these two super-close points.

The Magical Formula

Now for the magic trick! We need a formula to capture this zooming-in process. Prepare for some *mathematical elegance*!

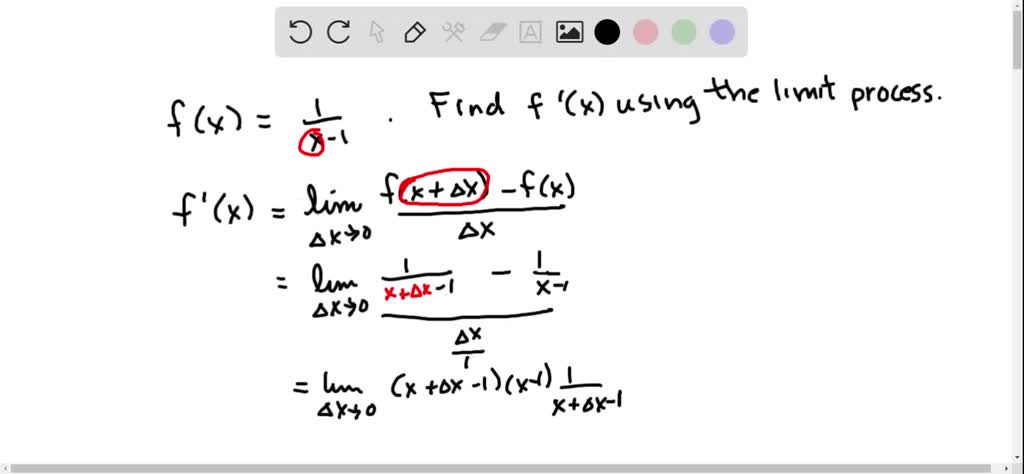
It looks like this: (f(x + h) - f(x)) / h. Sounds intimidating, right?

But don't you fret! Think of f(x) as the height of your roller coaster at position x.

And f(x + h) is the height at a point just a tiny bit further along, *h* being our super small distance!

The numerator, f(x + h) - f(x), calculates the change in height (the "rise"). The denominator, h, calculates the change in position (the "run").

The Limit: Approaching Infinity... of Awesomeness!

Now comes the key ingredient: the *limit*! We want to see what happens to that slope formula as *h* gets incredibly small, approaching zero. This is like getting closer and closer to the specific point on the roller coaster track.

We write it like this: lim (h->0) (f(x + h) - f(x)) / h.

This reads: "The limit as *h* approaches zero of (f(x + h) - f(x)) divided by *h*."

This limit gives us the *instantaneous rate of change* at a specific point.

Example Time: The Super Simple Case

Let's say our roller coaster is just a straight line: f(x) = 2x. Super boring, but perfect for illustrating this.

Plugging into our magical formula, we get: lim (h->0) (2(x + h) - 2x) / h.

Simplifying, we get: lim (h->0) (2x + 2h - 2x) / h = lim (h->0) 2h / h = lim (h->0) 2 = 2.

Ta-da! The derivative of 2x is 2. The slope is constant (it’s a straight line!), and our limit process heroically rescued us!

Derivatives: Unlocking the Secrets of Change

The derivative, found using the limit process, is super important. It tells us how quickly something is changing.

From physics (velocity and acceleration) to economics (marginal cost and revenue), derivatives unlock a world of insights!

So, next time you see a derivative, don't run away screaming! Remember our roller coaster and the joy of zooming in. Embrace the limit process! You've got this!