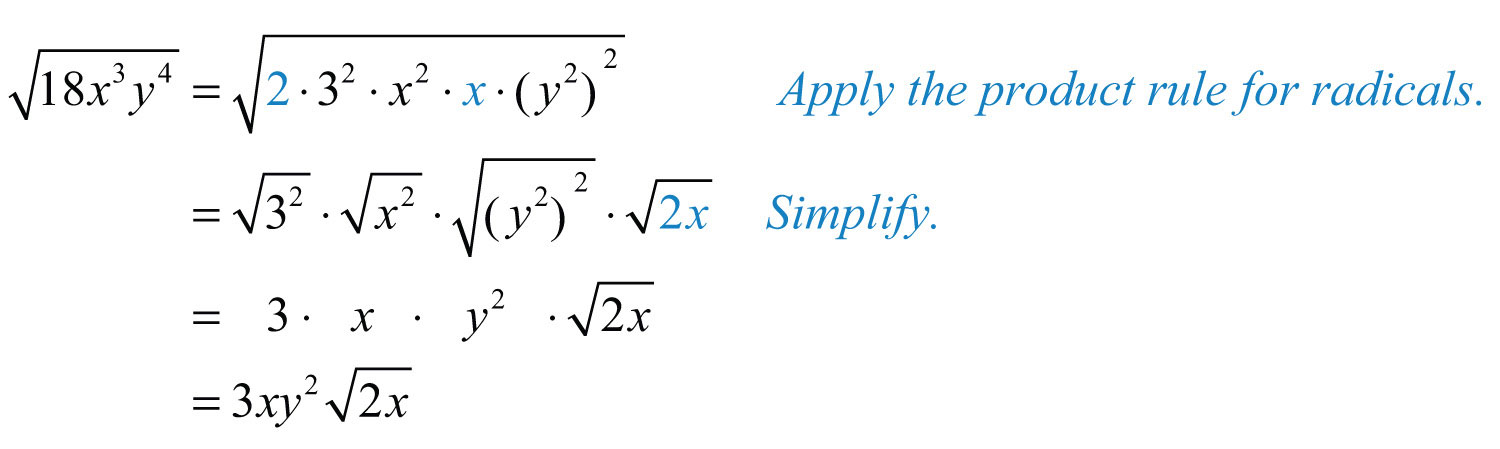How To Write Expressions In Radical Form
Let's talk about radicals, those sneaky little symbols that can make math look like pirate treasure maps. Think of them as mathematical containers holding secrets, ready to be unlocked!
First, imagine you have a number like, say, 8. We want to write this in radical form, but without actually changing its value. It's like dressing up a potato as a princess – still a potato, just fancier.
Finding the Perfect Square
The key to this magical makeover is finding a perfect square that divides evenly into our number. A perfect square is a number that results from squaring another number (1, 4, 9, 16, 25, and so on).
For 8, the perfect square that works is 4, because 8 = 4 * 2. See where we are going?
Now, let's introduce our radical friend: the square root symbol, looking all stylish like a check mark with a long tail √.
The Radical Transformation
We can rewrite our expression using the square root of 4 times 2. This will be √ (4*2).
The next step is radical separation! Since we have the square root of a product, we can split it into the product of the square roots: √4 * √2.
Now for the fun part: We know that the square root of 4 is 2. Therefore, √4 * √2 becomes 2 * √2, or simply 2√2. Ta-da! 8, disguised as 2√2.
Dealing with Bigger Numbers
Let's try a bigger number, maybe 50. The perfect square that divides into 50 is 25 (50 = 25 * 2).
So, we can express this in radical form: √50 = √(25*2) = √25 * √2 = 5√2.
It's like finding hidden treasures within numbers! Isn't it fun?
Expressions with Variables
Now let's get a little wild and try something with a variable! How about x3?
Remember, the goal is to find perfect squares. If we have x3, we can rewrite it as x2 * x.
Then, we'll put it under radical form: √(x2 * x) = √x2 * √x = x√x. Isn’t it cool?
A Few Tips and Tricks
Always look for the largest possible perfect square. Finding the largest perfect square makes simplifying easier.
Don't be afraid to experiment! The journey of figuring out the simplest radical form is much more fun than the destination.
Sometimes, the number is already in its simplest form. For instance, 7 is a prime number. It cannot be divided by any perfect square. So, it stays as √7.
Radicals Are Everywhere!
You might be wondering: why are we even doing this? Well, radicals pop up in geometry (think the Pythagorean Theorem), physics, and even computer graphics!
Understanding how to manipulate them opens doors to a whole new world of mathematical possibilities.
So, go forth and conquer those radicals. You are now an expert at dressing up numbers in their radical finest!
Remember to have fun with radical expressions!