58 Rounded To The Nearest Ten
The number 58, rounded to the nearest ten, is not merely a mathematical exercise; it represents a fundamental concept impacting everyday calculations, statistical analysis, and even policy decisions. Its seemingly simple resolution – 60 – masks the underlying principles of rounding, which have far-reaching consequences in data interpretation and numerical approximations across various disciplines.
At its core, rounding aims to simplify numbers, making them easier to work with while accepting a degree of imprecision. The crux lies in understanding the rules that govern this simplification and acknowledging the potential impact of the resulting approximation. This article delves into the mechanics of rounding 58 to the nearest ten, examines its applications, and explores the inherent limitations and potential pitfalls of this ubiquitous mathematical operation. We will also briefly look at how rounding impacts real-world scenarios like financial calculations, scientific estimations and the statistical interpretation of data.
The Mechanics of Rounding: A Deep Dive
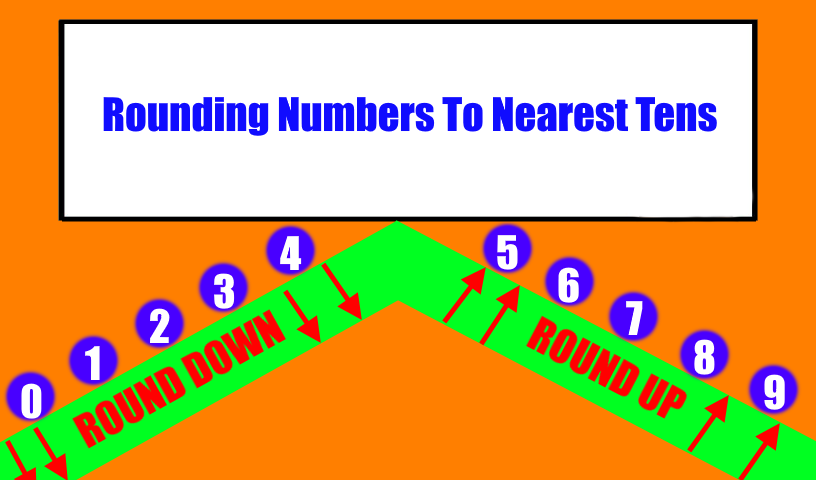
Rounding to the nearest ten involves identifying the two multiples of ten closest to the number in question – in this case, 50 and 60. The decision of which multiple to choose hinges on the digit in the ones place. In the case of 58, that digit is 8.
The standard rounding rule dictates that if the ones digit is 5 or greater, the number is rounded up to the higher multiple of ten. Conversely, if the ones digit is less than 5, the number is rounded down to the lower multiple of ten. Therefore, since 8 is greater than 5, 58 is rounded up to 60.
This principle extends to other rounding scenarios as well, such as rounding to the nearest hundred, thousand, or even decimal place. The key is always to identify the relevant digit and compare it to the halfway point (typically 5) between the two nearest multiples.
Applications of Rounding in Real-World Scenarios
Rounding is an essential tool in various fields. In finance, for example, large sums of money are often rounded to the nearest thousand or million to simplify reporting and analysis.
In scientific research, rounding can be used to present data in a more understandable format. For instance, the average height of a population might be rounded to the nearest centimeter.
Furthermore, rounding is frequently employed in statistical analysis to aggregate data and identify trends. This can provide quick insights into patterns that might not be immediately apparent when working with raw numbers. As stated by Dr. Anya Sharma, a statistician at the National Institute of Mathematics, "Rounding allows us to effectively communicate complex data in a more digestible manner, revealing underlying trends and patterns that may be obscured by excessive precision."
The Impact of Rounding Errors: A Word of Caution
While rounding offers benefits in terms of simplification and clarity, it also introduces the potential for errors. Each time a number is rounded, a small amount of information is lost.
If rounding is applied repeatedly over many calculations, these small errors can accumulate and lead to significant discrepancies. This is particularly relevant in situations involving large datasets or complex models.
Professor David Chen, an economist at Stanford University, warns, "It is crucial to understand the implications of rounding, especially when dealing with financial models or economic forecasts. Repeated rounding can propagate errors and distort the accuracy of the final results." This risk is compounded in large-scale models where many rounded inputs contribute to a final aggregate number, where the accumulative rounding errors can be significant. To mitigate these errors, it's vital to retain as much precision as possible until the final calculation stage and implement strategies to track and minimize rounding errors.
Alternative Rounding Methods and Their Significance
While the standard rounding rule (rounding up at 5 or above) is the most common, alternative methods exist and are used in various contexts. One such method is "round half to even," also known as banker's rounding.
This method aims to reduce bias in calculations by rounding numbers ending in 5 to the nearest even number. This approach distributes rounding errors more evenly, and it reduces the overall statistical bias during extensive statistical operation. This method is particularly relevant in statistical analysis and scientific computations, where minimizing bias is critical.
Another method is rounding down. Rounding down is more common when precision is very important. Consider the case of purchasing construction materials. Rounding down guarantees that you do not purchase less than you need, even if you are required to purchase extra.
Looking Ahead: The Future of Rounding and Numerical Approximations
As computational power continues to increase, the need for manual rounding may decrease in some areas. Modern software and algorithms can handle large datasets with high precision, reducing the reliance on simplified approximations. However, the underlying principles of rounding will remain relevant.
Even with advanced technology, the ability to understand and interpret rounded numbers is crucial for effective communication and decision-making. Furthermore, understanding the potential limitations of rounding errors will become increasingly important as data-driven decision-making becomes more prevalent.
The seemingly simple question of "58 rounded to the nearest ten" serves as a reminder of the importance of mathematical literacy and the need for a nuanced understanding of numerical approximation techniques. Whether dealing with financial statements, scientific data, or everyday calculations, the principles of rounding will continue to shape how we interpret and utilize numbers in the modern world.
