90 As A Product Of Prime Factors

In a seemingly simple mathematical exercise, the number 90 has recently become the focus of attention as educators and math enthusiasts delve into its prime factorization. This exploration highlights the fundamental building blocks of numbers and offers a practical application for understanding more complex mathematical concepts.

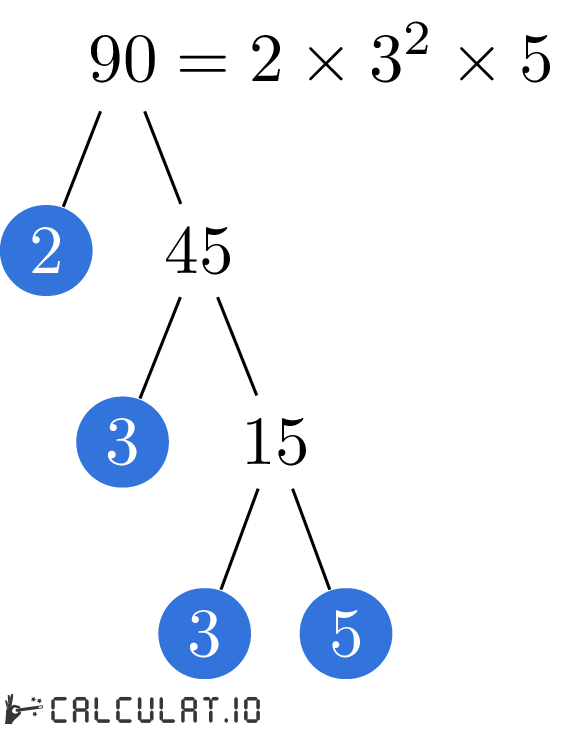
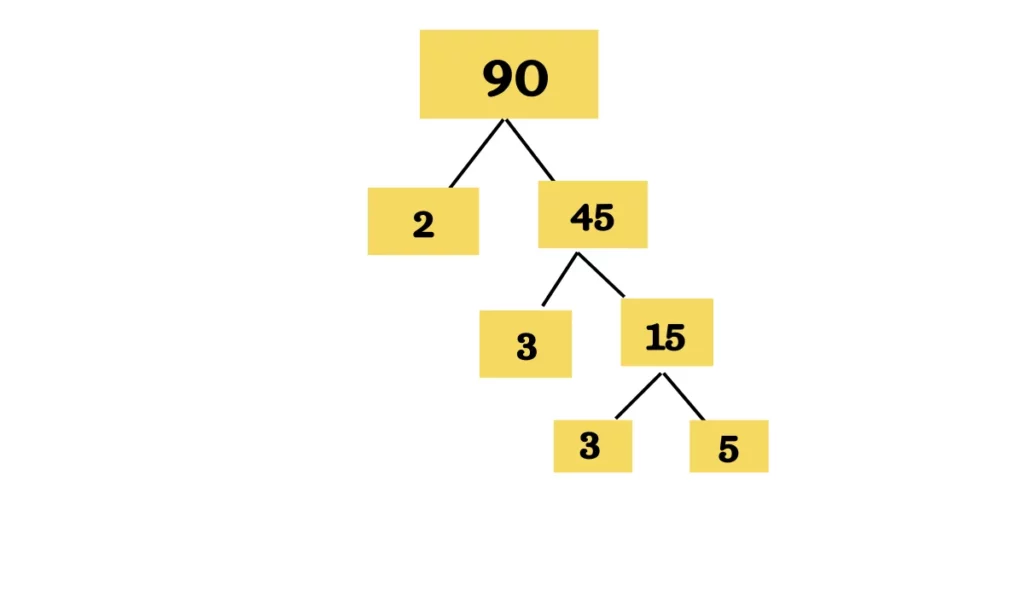
The prime factorization of 90, expressed as 2 x 3 x 3 x 5, or 2 x 3² x 5, serves as a valuable illustration for teaching prime numbers and factorization techniques. Understanding this concept is crucial for grasping broader mathematical principles such as greatest common divisors, least common multiples, and algebraic simplification.

Prime Factorization: The Core Concept

Prime factorization involves breaking down a composite number into its prime number components. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on.

The process of prime factorization involves successively dividing a number by prime numbers until all factors are prime. In the case of 90, we can start by dividing it by the smallest prime number, 2. This gives us 90 ÷ 2 = 45.

Next, we look at 45. It's not divisible by 2, so we move to the next prime number, 3. We find that 45 ÷ 3 = 15. Again, 15 is divisible by 3, giving us 15 ÷ 3 = 5.

Finally, 5 is a prime number itself, so we've reached the end of the process. The prime factors of 90 are thus 2, 3, 3, and 5, or 2 x 3² x 5.

Educational Significance

Understanding the prime factorization of numbers like 90 is a foundational skill in mathematics education. It provides a concrete example of how composite numbers are constructed from prime numbers. This knowledge helps students develop a deeper understanding of number theory.

Prime factorization is essential for simplifying fractions. Students can easily identify common factors in the numerator and denominator, leading to simplified forms. This is particularly helpful in more complex algebraic equations.

Furthermore, it provides a tool for calculating the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. These concepts are crucial in fields like cryptography and computer science.

Applications in Cryptography and Computer Science

Prime numbers and their properties play a significant role in cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring large numbers into their prime factors.

In computer science, prime factorization is used in algorithms for hashing, data compression, and other computational tasks. Understanding prime numbers and their characteristics can lead to more efficient and optimized algorithms.

"Prime factorization is not just an abstract concept; it's a powerful tool with real-world applications," said Dr. Anya Sharma, a mathematics professor at State University. "It's crucial for students to grasp these fundamentals early on to build a strong foundation in mathematics."

Teaching Strategies

Educators employ various strategies to teach prime factorization effectively. These range from hands-on activities using manipulatives to visual aids like factor trees.

Factor trees are a common method where a number is broken down into its factors branch by branch until all branches end in prime numbers. This visual representation can make the concept more accessible to visual learners.

Another approach involves using games and puzzles to make learning engaging and fun. These activities can help students practice prime factorization without even realizing they are doing math.

The Human Element: Making Math Relatable

To further enhance the learning experience, educators often try to connect mathematical concepts to real-life situations. For example, students might be asked to determine the number of ways to arrange 90 identical items into rectangular arrays.

Another exercise is to have students design a garden with 90 plants, arranging them in rows and columns where the number of plants in each row and column are prime numbers. Such exercises make math more relatable and meaningful.

By exploring the prime factors of a number like 90, educators can create engaging lessons that highlight the usefulness and relevance of mathematics. The act of doing this makes math more fun and less daunting.

Conclusion

The prime factorization of 90, while seemingly simple, provides a crucial entry point into more advanced mathematical concepts. Its application extends far beyond the classroom, with implications in cryptography, computer science, and various other fields.

By understanding the building blocks of numbers, students develop a stronger foundation for future mathematical endeavors. Thus, prime factorization remains a relevant and important topic in mathematics education.

As we continue to advance in technology and science, the fundamental principles of mathematics will remain vital for innovation and progress. Numbers like 90, broken down to their prime components, serve as a reminder of the elegance and power of mathematical thinking.