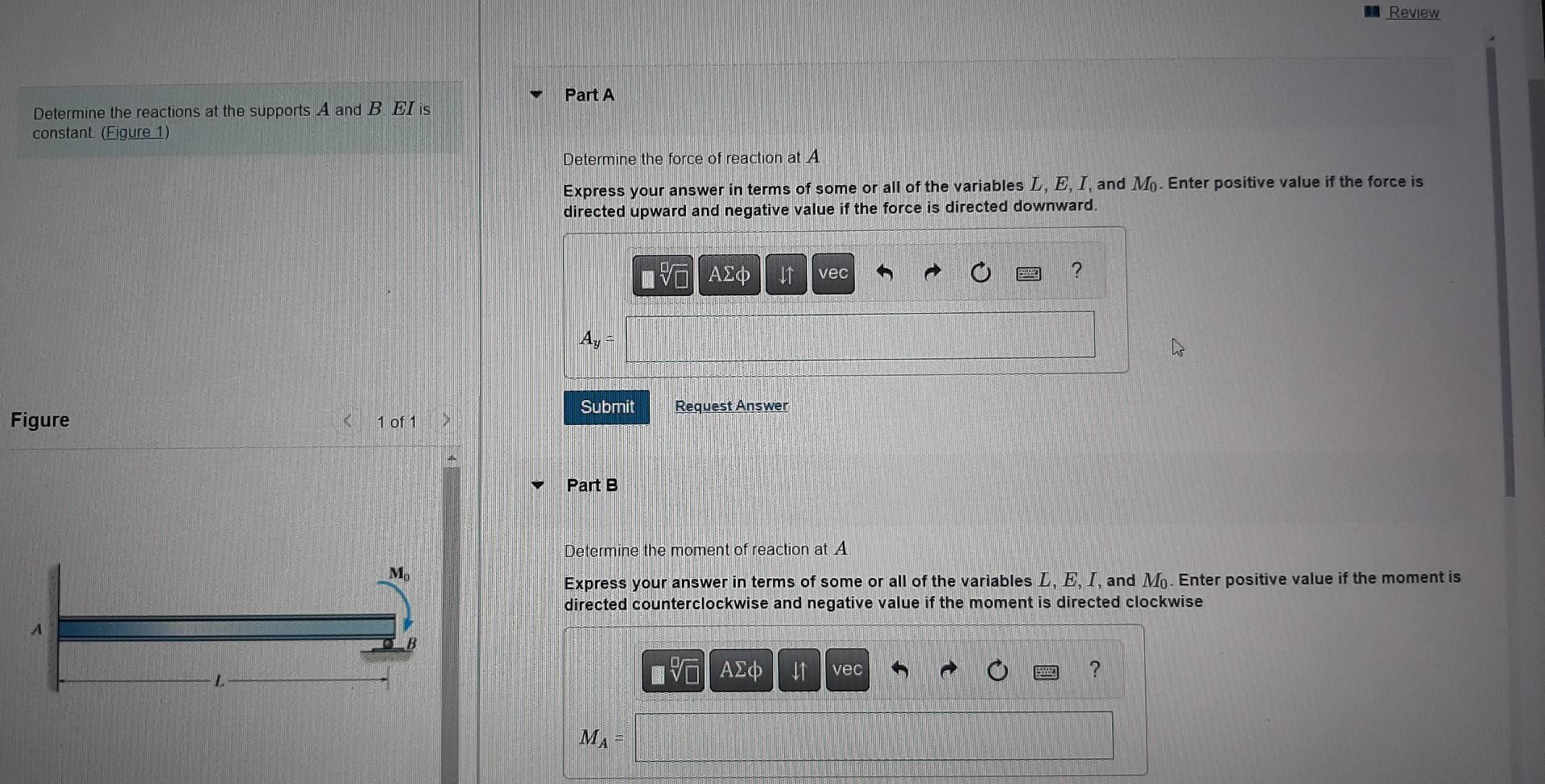
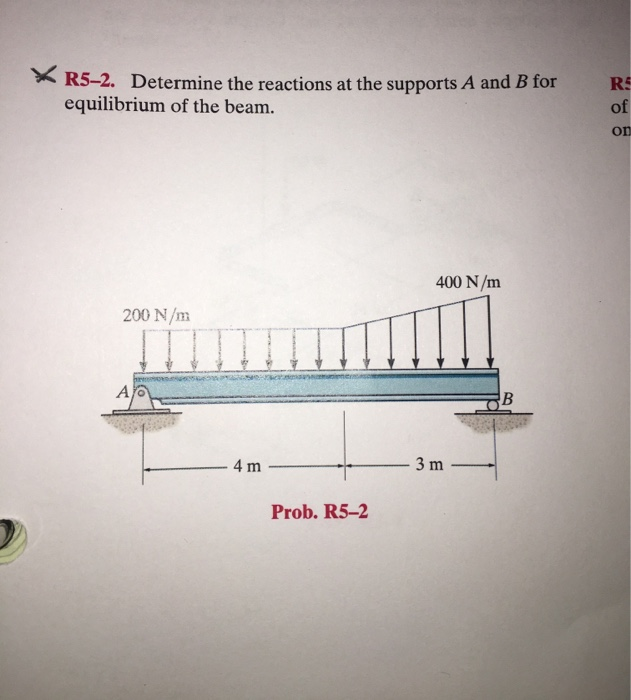
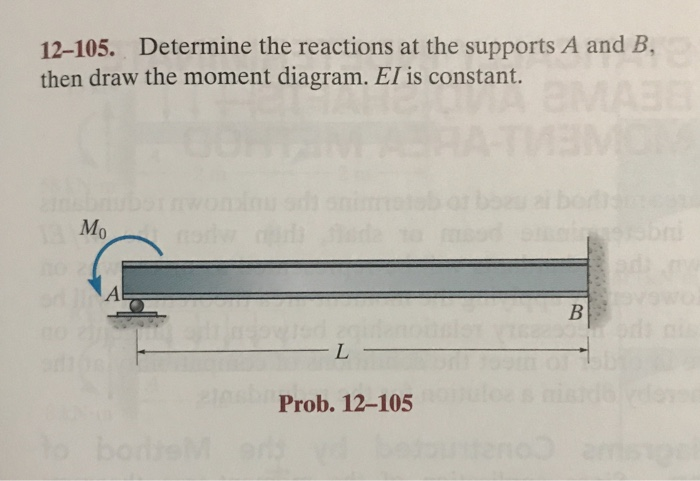
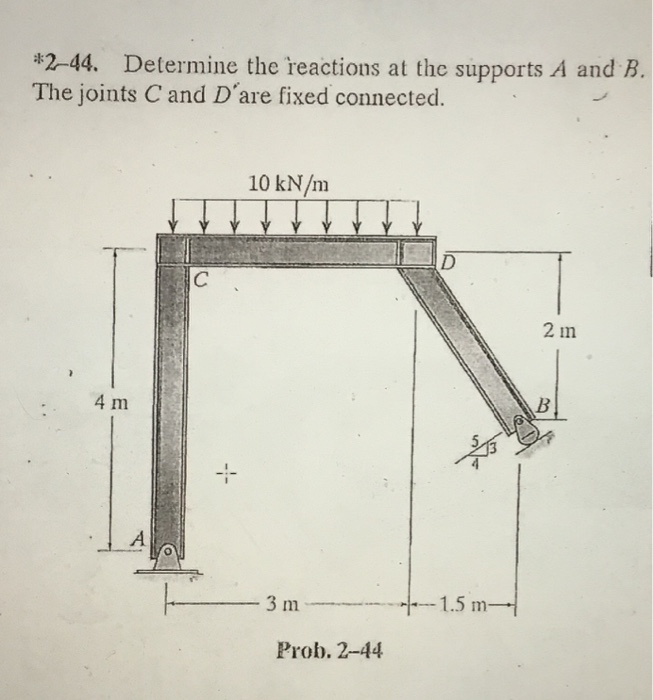
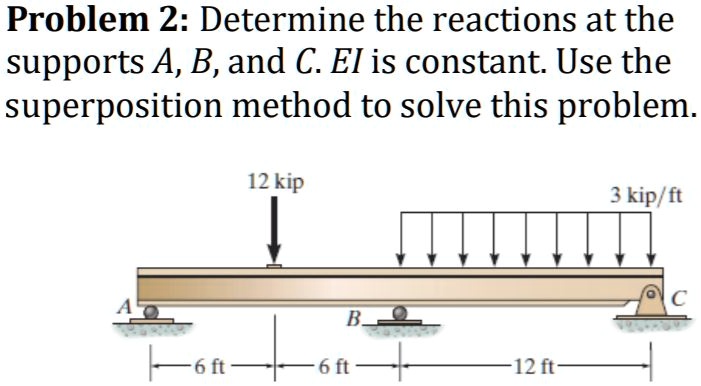
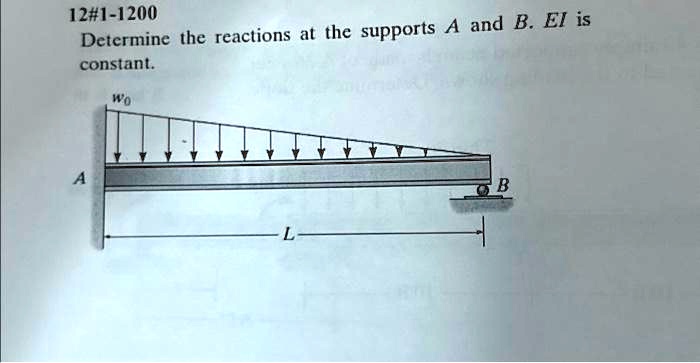
Determine The Reactions At The Supports A And B
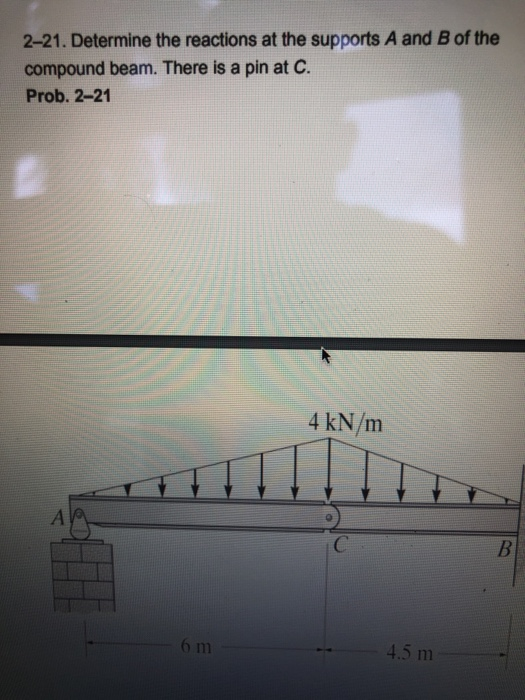
Structural engineers and civil engineering students worldwide are grappling with a complex statics problem involving a simply supported beam. The challenge focuses on accurately determining the reactions at supports A and B under various loading conditions. This problem serves as a foundational exercise in structural analysis and is crucial for understanding the principles of equilibrium.
The problem, typically presented in introductory mechanics courses, involves a horizontal beam resting on two supports, A and B. Students are tasked with calculating the vertical forces exerted by these supports in response to applied loads on the beam. The loads can range from simple point loads to more complex distributed loads, making the problem progressively challenging.
The key to solving this problem lies in applying the principles of static equilibrium.
Core Principles
Static equilibrium dictates that for a body to be at rest, the sum of all forces and moments acting on it must be zero. This translates into two fundamental equations for a two-dimensional problem: the sum of forces in the vertical direction must equal zero (ΣFy = 0), and the sum of moments about any point must equal zero (ΣM = 0). These equations form the basis for solving for the unknown reactions at supports A and B.
Applying Equilibrium Equations
To determine the reactions, engineers and students typically follow a structured approach. First, a free body diagram of the beam is drawn, showing all external forces and the unknown reactions at the supports. Second, the equilibrium equations are applied, and the resulting system of equations is solved for the unknown reaction forces RA (reaction at A) and RB (reaction at B).
The complexity arises when dealing with distributed loads. In these cases, the distributed load must be converted into an equivalent point load before applying the equilibrium equations.
Importance of Accuracy
The accurate determination of support reactions is paramount in structural design. Overestimation or underestimation of these forces can lead to structural failure. Understanding the distribution of loads and their effect on supports is crucial for ensuring the stability and safety of any structure. This underscores the significance of mastering these concepts at an early stage of engineering education.
Professor Eleanor Vance, a leading expert in structural mechanics at the University of California, Berkeley, emphasizes the critical role of this problem. "Understanding support reactions is fundamental to all structural analysis," she stated. "It's the foundation upon which we build more complex calculations. Accurate assessment is not merely an academic exercise; it directly impacts the integrity and safety of real-world structures."
Mistakes in determining support reactions can have severe consequences. Underestimating the reactions can lead to under-designed supports, which may fail under load. Overestimating the reactions, while generally safer, can result in over-designed supports, leading to unnecessary costs and inefficient use of materials.
Real-World Applications
The concepts learned from solving this problem are applicable across various engineering disciplines. Civil engineers use these principles to design bridges, buildings, and other infrastructure. Mechanical engineers apply them to design machine components and support structures. Aerospace engineers use them to design aircraft and spacecraft structures.
One notable example is in the design of bridge supports. Bridge designers must accurately determine the reactions at the bridge piers (supports) to ensure the bridge can withstand the weight of traffic and environmental loads such as wind and snow.
Understanding these principles allows engineers to make informed decisions about the size and material of supports, as well as the overall design of the structure.
Tools and Resources
Numerous tools and resources are available to assist in solving these types of problems. Software such as AutoCAD, SAP2000, and ANSYS can be used to model and analyze structures. These tools can automate the calculations and provide graphical representations of the results, aiding in visualization and understanding.
However, engineers and students are encouraged to first solve these problems manually to develop a solid understanding of the underlying principles. This hands-on approach helps solidify the concepts and develop critical thinking skills. Textbooks and online tutorials offer a wealth of information and examples.
Websites like Khan Academy and Coursera provide free courses on statics and mechanics, covering the fundamental principles and problem-solving techniques.
Conclusion
The problem of determining reactions at supports A and B is a cornerstone of structural analysis. While seemingly simple, it encapsulates the fundamental principles of static equilibrium and their application in real-world engineering scenarios. Mastering this problem is essential for anyone pursuing a career in structural, civil, mechanical, or aerospace engineering.
The exercise reinforces the importance of accuracy, attention to detail, and a thorough understanding of the underlying physics. Ultimately, proficiency in solving this problem translates into safer and more efficient designs in various engineering fields. By focusing on the core concepts, engineers and students can develop the skills necessary to tackle even more complex structural challenges.
Continued practice and engagement with these fundamental problems are key to building a strong foundation in structural engineering.


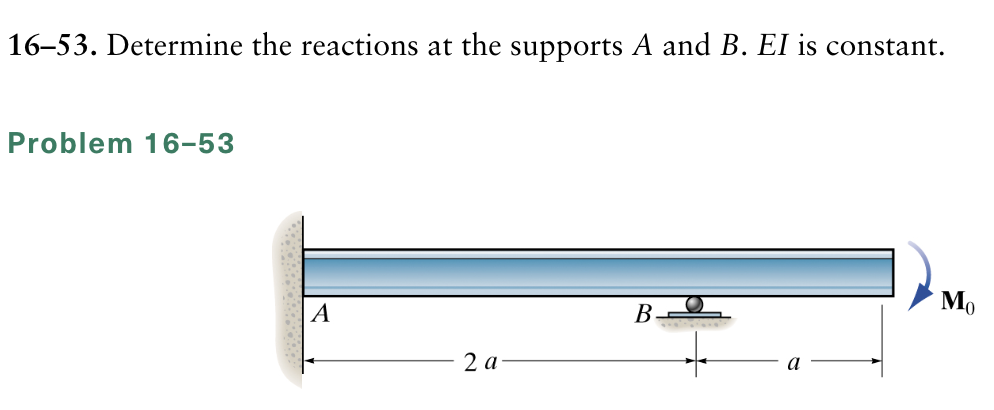
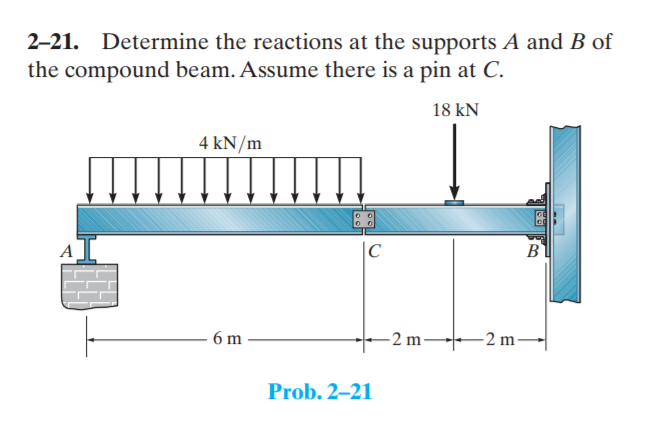
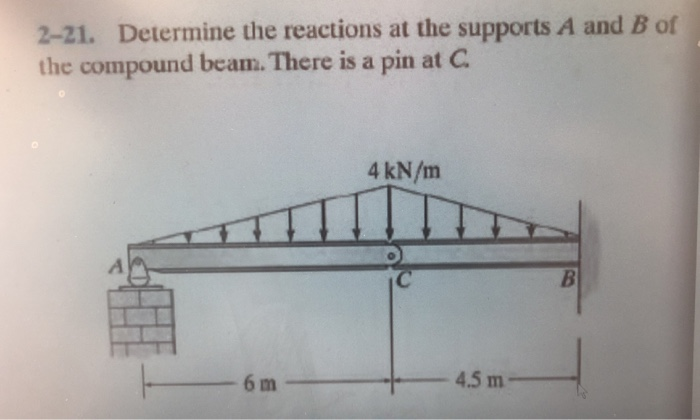

![Determine The Reactions At The Supports A And B [Solved]: Determine the reactions at the supports A and B.E](https://media.cheggcdn.com/media/658/6585d9a8-1283-41cd-a69b-fb33119b0c6d/Screenshot2024-05-20000406.png)