Find The Prime Factors Of 50

In an era dominated by quantum computing and the relentless pursuit of ever-more-complex algorithms, a seemingly simple mathematical problem has unexpectedly captured public attention. The challenge? Decomposing the number 50 into its prime factors. This seemingly trivial exercise has sparked debate and reflection on the fundamental principles underlying modern cryptography and data security.

At first glance, the decomposition of 50 may appear to be a straightforward academic exercise. However, the renewed interest stems from the growing realization that the computational difficulty of factoring large numbers into their prime components forms the bedrock of widely used encryption methods. The relative ease with which 50 can be factored serves as a stark reminder of the vulnerabilities that exist when dealing with significantly larger numbers, potentially jeopardizing sensitive information and digital infrastructure.

The Prime Factorization of 50: A Mathematical Breakdown

The prime factorization of a number is the process of expressing it as a product of prime numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Common examples include 2, 3, 5, 7, 11, and so on.

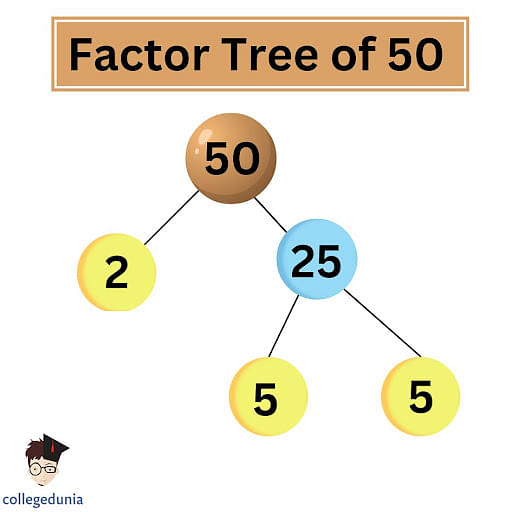
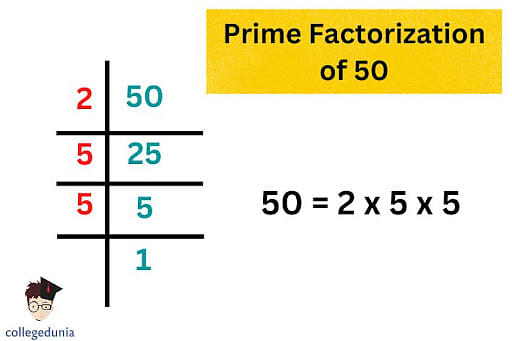
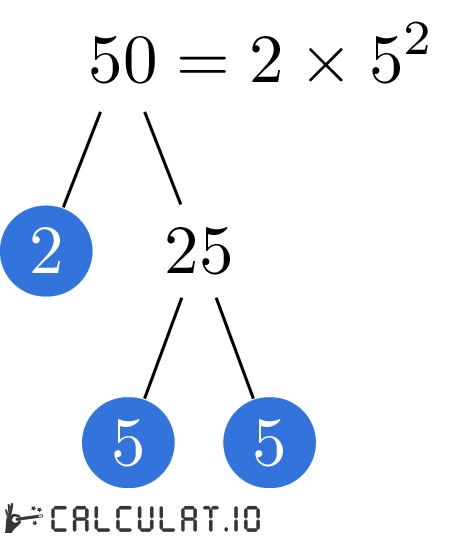
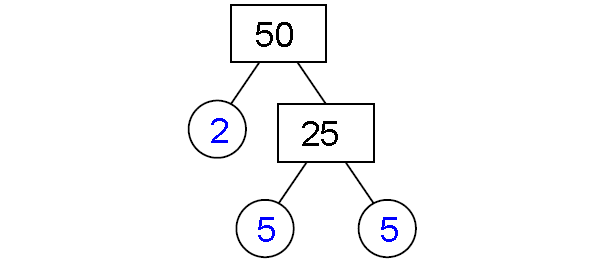
To determine the prime factors of 50, one begins by identifying the smallest prime number that divides 50 evenly. That number is 2. Dividing 50 by 2 yields 25.

Next, we consider the number 25. The smallest prime number that divides 25 evenly is 5. Dividing 25 by 5 yields 5, which is itself a prime number.

Therefore, the prime factorization of 50 is 2 x 5 x 5, or 2 x 5². This can be expressed concisely as: 50 = 2 x 5².

Implications for Cryptography

The seemingly simple task of finding the prime factors of 50 highlights a critical concept in cryptography. Many modern encryption algorithms, such as RSA, rely on the difficulty of factoring large numbers into their prime components.

The security of RSA hinges on the fact that while it is relatively easy to multiply two large prime numbers together, it is computationally very difficult to reverse the process—that is, to find the prime factors of a very large composite number. The larger the prime numbers used, the more secure the encryption.

The exercise with 50 demonstrates this principle on a smaller scale. While easily factorable, it illustrates how the complexity escalates dramatically as the numbers involved increase in size.

Expert Opinions and Perspectives

Dr. Anya Sharma, a leading cryptographer at the National Institute of Standards and Technology (NIST), emphasized the importance of understanding the fundamentals of prime factorization. "While breaking down 50 is trivial, it underscores the core principle behind many encryption schemes," she stated. "It's a valuable exercise for students and professionals alike."

Professor Ben Carter from Stanford University's Computer Science Department added a cautionary note. "The ease with which 50 can be factored should serve as a reminder that encryption algorithms are not unbreakable. Advancements in computing power, particularly in quantum computing, pose a significant threat to current encryption methods."

Indeed, the emergence of quantum computers, which leverage the principles of quantum mechanics to perform computations far beyond the capabilities of classical computers, represents a potential game-changer. Shor's algorithm, a quantum algorithm, can theoretically factor large numbers much more efficiently than any known classical algorithm, jeopardizing the security of RSA and other widely used cryptographic systems.

The Future of Encryption

The renewed focus on prime factorization has spurred research into new encryption methods that are resistant to quantum attacks. These methods, known as post-quantum cryptography (PQC), are designed to be secure even if a quantum computer were to become available.

NIST is currently leading a global effort to develop and standardize PQC algorithms. These algorithms are based on mathematical problems that are believed to be difficult even for quantum computers, such as lattice-based cryptography and code-based cryptography.

The transition to PQC is a complex and ongoing process. It requires careful evaluation of the security and performance of candidate algorithms, as well as the development of new cryptographic protocols and standards.

Conclusion: A Foundation for Future Security

While the prime factorization of 50 may seem like a simple mathematical curiosity, it provides a valuable insight into the foundations of modern cryptography. It highlights both the power and the limitations of current encryption methods, and it underscores the need for ongoing research and development in the field of cybersecurity.

As technology continues to evolve, particularly with the advent of quantum computing, it is crucial to understand the underlying principles of prime factorization and their implications for data security. This understanding is essential for developing robust encryption methods that can protect sensitive information in an increasingly complex and interconnected world.

The seemingly simple act of factoring 50 serves as a powerful reminder that the quest for secure communication is a continuous journey, one that requires constant vigilance and innovation.