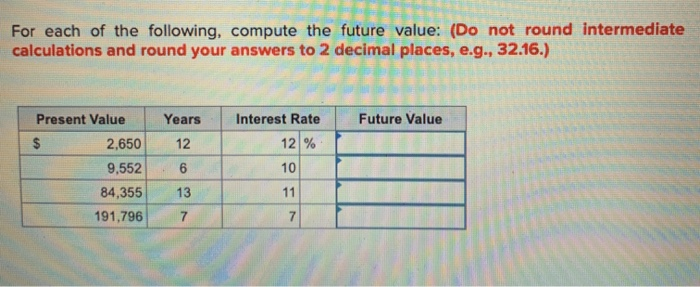
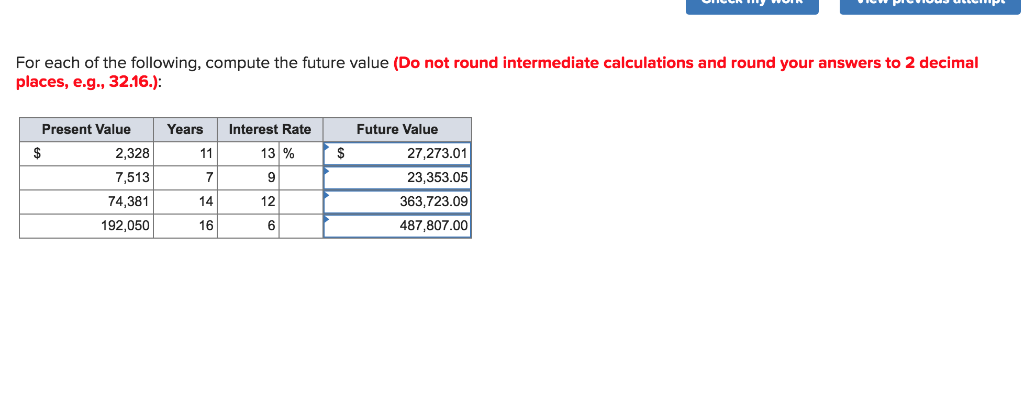
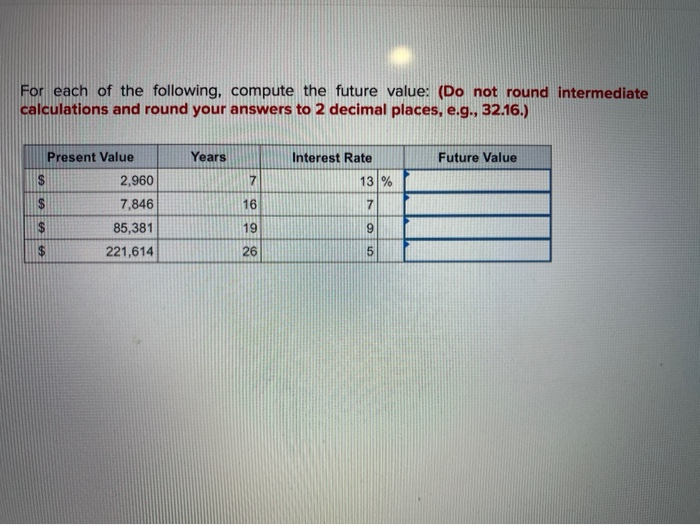
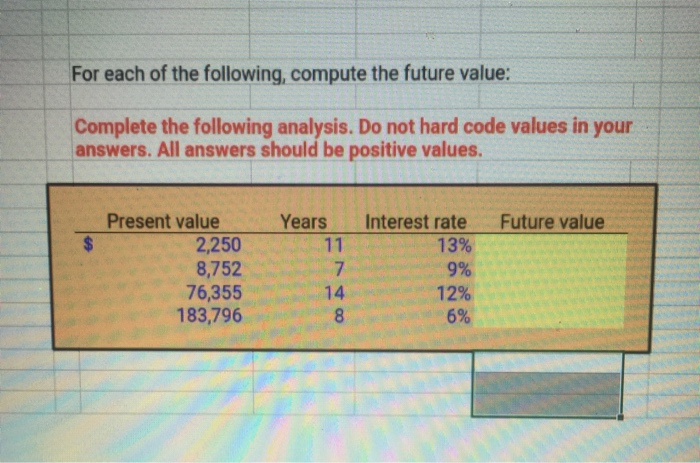
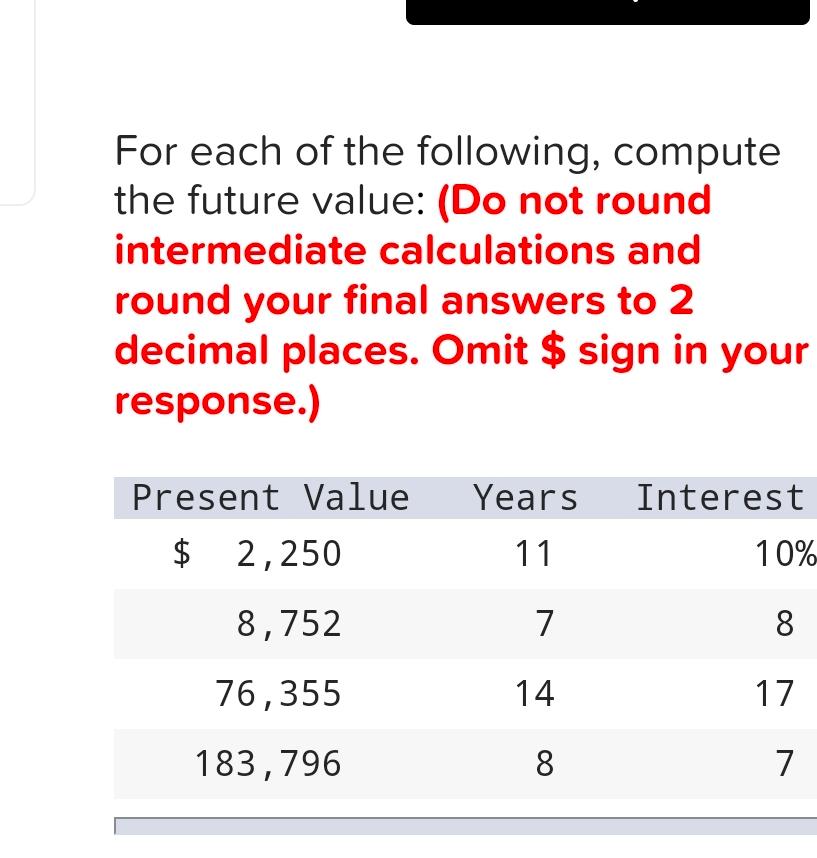
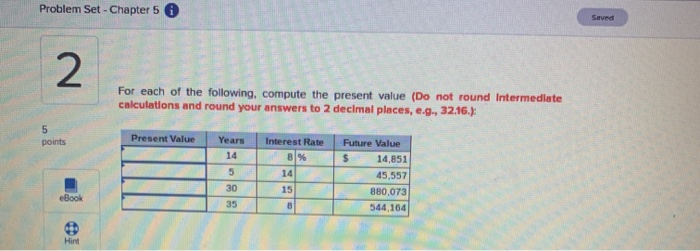
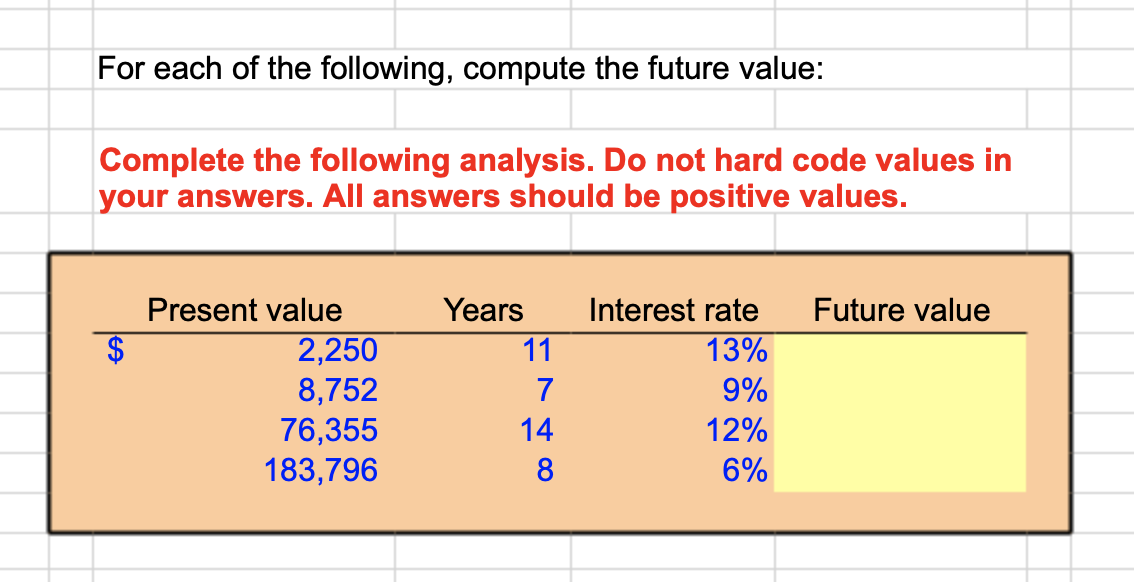
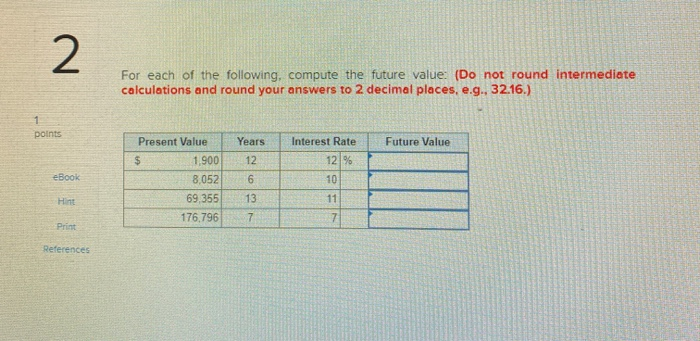
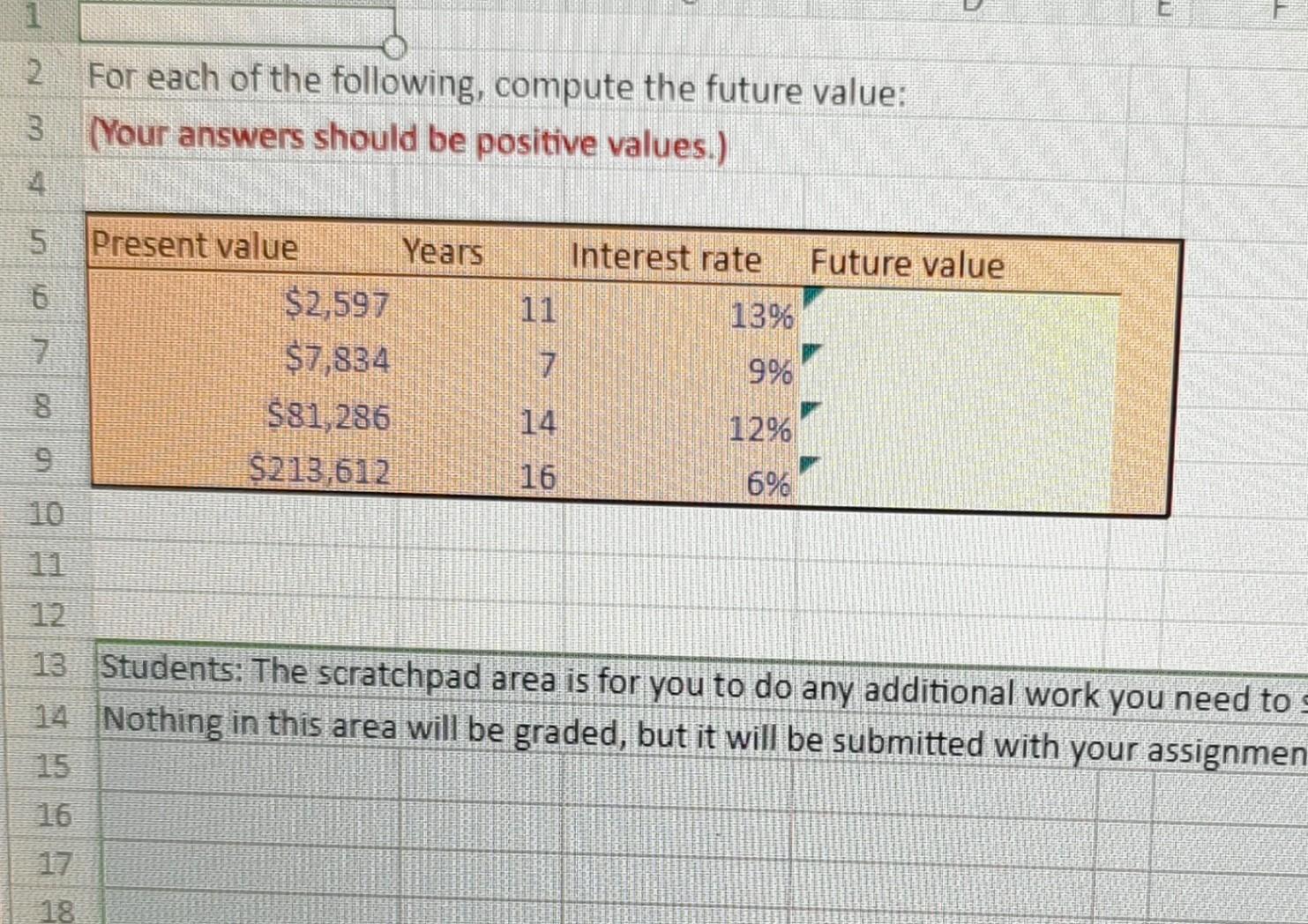
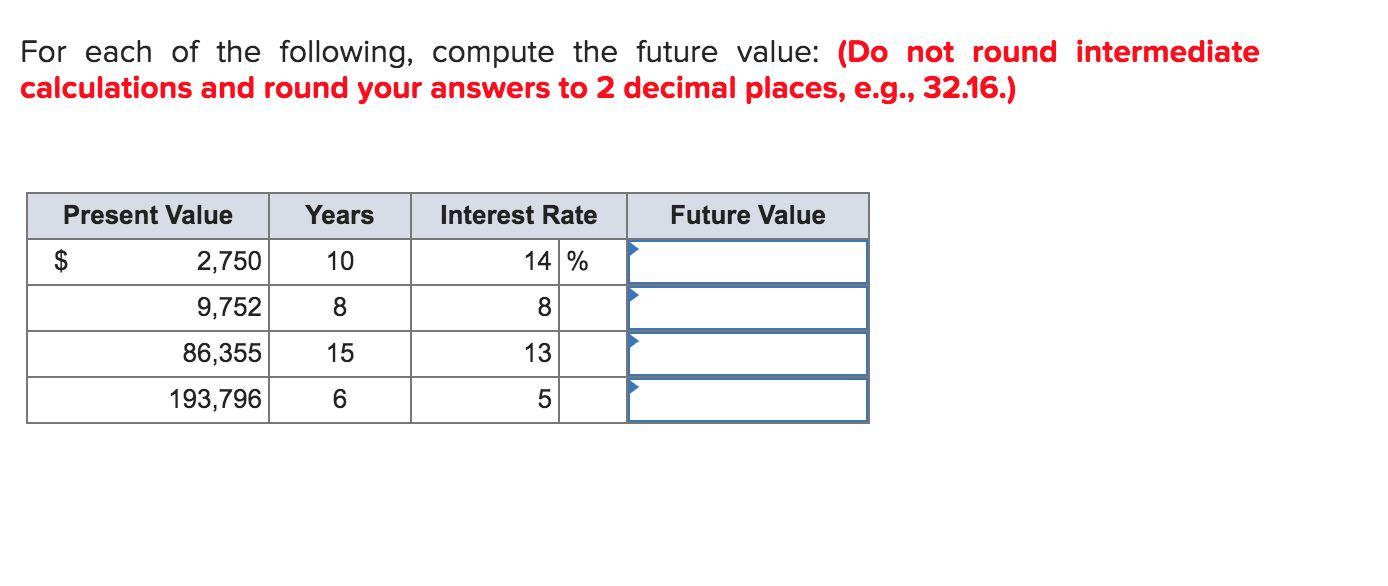
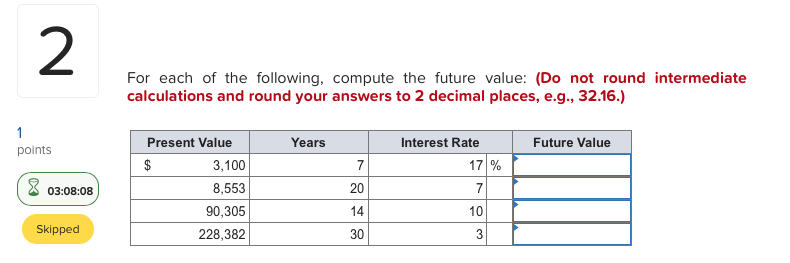
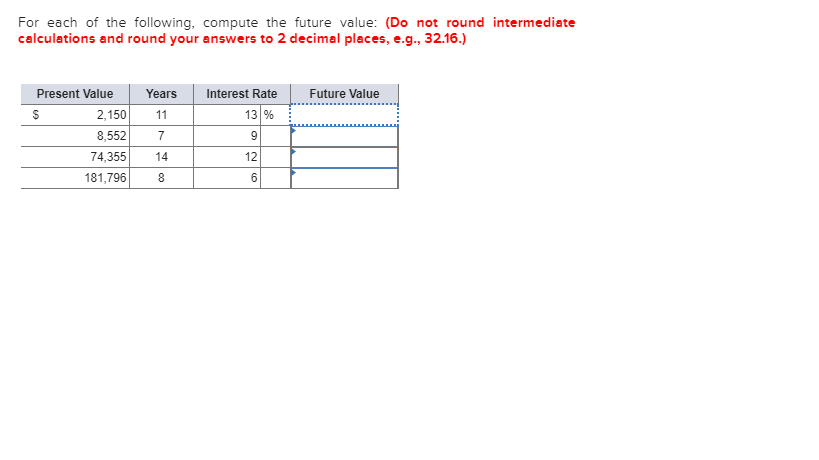
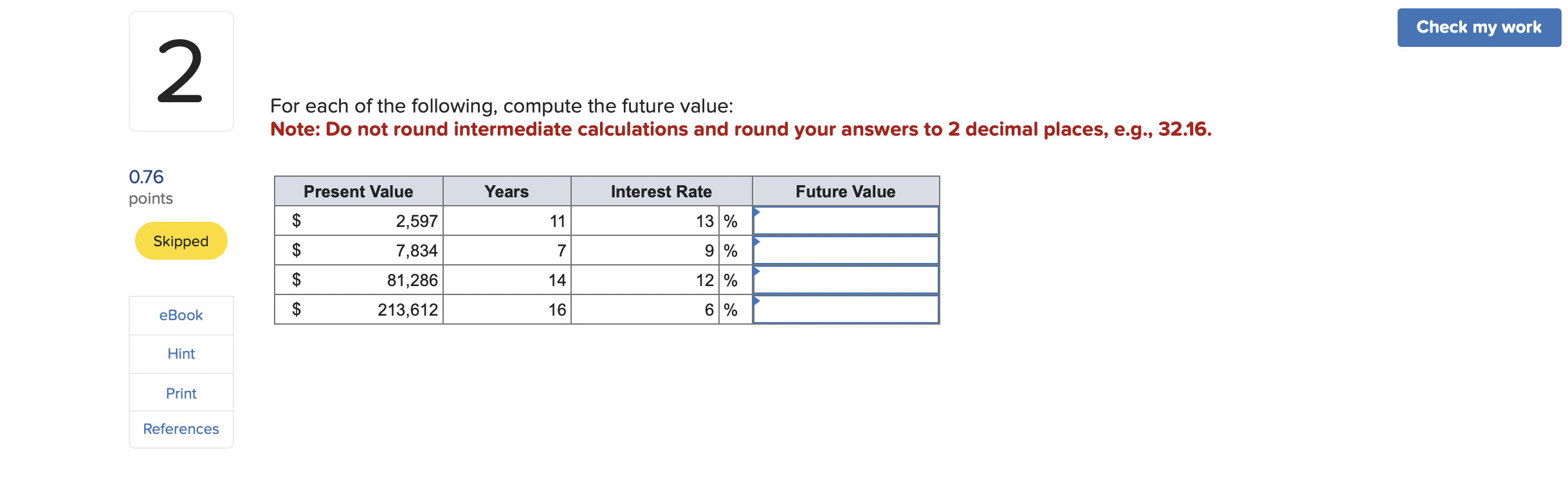
For Each Of The Following Compute The Future Value

Urgent financial advisory: Individuals and businesses face a critical juncture, requiring immediate action to secure future financial stability. Misunderstanding future value calculations can lead to severe economic repercussions, impacting investment strategies and long-term savings goals.

This article provides a concise guide to calculating future value (FV) for diverse financial scenarios, ensuring readers can make informed decisions to protect and grow their assets in an uncertain economic climate.

Scenario 1: Simple Interest Investment

What: Calculating the future value of a $1,000 investment at a simple interest rate.

How: An investment of $1,000 earning 5% simple interest annually for 5 years yields a future value of $1,250. The formula is FV = P(1 + rt), where P = principal, r = interest rate, and t = time.

This straightforward calculation highlights the basic growth of capital over time with simple interest accumulation. Understanding this is crucial before engaging in more complex financial instruments.

Scenario 2: Compound Interest Investment

What: Determining the future value of a $5,000 investment compounded annually.

How: Investing $5,000 at an annual interest rate of 7%, compounded annually for 10 years, results in a future value of $9,835.76. Use FV = P(1 + r)^n, where n = number of compounding periods.

This demonstrates the power of compounding, significantly increasing returns compared to simple interest over longer durations.

Scenario 3: Compounding Frequency Impact

What: Comparing future values based on different compounding frequencies.

How: A $2,000 investment at 6% annual interest for 3 years, compounded quarterly, results in a future value of $2,393.41. The formula adjusts to FV = P(1 + r/m)^(mt), where m = number of compounding periods per year.

Increasing the compounding frequency, from annually to quarterly, enhances the overall return due to more frequent interest accrual. Always compare the impact of different compouding options.

Scenario 4: Future Value of an Annuity

What: Calculating the future value of a series of regular deposits (an annuity).

How: Contributing $500 annually into an account earning 8% interest for 20 years generates a future value of $22,880.40. The formula is FV = P * [((1 + r)^n - 1) / r].

Annuities are crucial for long-term savings plans, such as retirement accounts, emphasizing the benefits of consistent investment.

Scenario 5: Impact of Inflation

What: Considering inflation when estimating future value.

How: An investment of $10,000 projected to be worth $16,000 in 10 years, with an average annual inflation rate of 3%, has a real future value of approximately $11,939.64 (present value terms). We account the impact of inflation into future value calculation to determine the real purchasing power.

Inflation erodes purchasing power; therefore, factoring it into FV calculations provides a more accurate representation of future wealth.

Scenario 6: Loan Amortization

What: Determine the future value of remaining balance after making payments for loan.

How: A loan of $20,000 with annual interest rate 6% amortized over 5 years. The remaining balance after paying 36 months (3 years) is $9,190.32. The balance is the present value of remaining payments.

Understanding the remaining balance on loan allows for strategies for either early repayment or refinancing.

Scenario 7: Deferred Annuity

What: Calculating future value when the investment begins later.

How: Contributing $2,000 annually for 10 years, but beginning in 5 years, at 9% interest. The $2,000 annual deposit starts 5 years from now for the next 10 years results a future value of $30,385.85.

The 5 year no deposit allows the initial amount to grow. This can be a critical aspect of retirement planning.

Scenario 8: Uneven Cash Flow

What: How to calculate the future value when cashflow is not equal.

How: An investment that generates $1000 in year 1, $1500 in year 2, and $2000 in year 3 with 7% annually. The total future value is $4,933.50. This calculation requires summing the future values of each individual cashflow.

Uneven cash flows are commong with investments that depend on economic trends. Using the right calculation is crucial to assess whether the investment is worthy.

Next Steps: Consult with a financial advisor to tailor these calculations to your specific circumstances and develop a comprehensive financial plan. Failure to act decisively now could jeopardize your financial future. Stay tuned for updated financial guidance as economic conditions evolve.