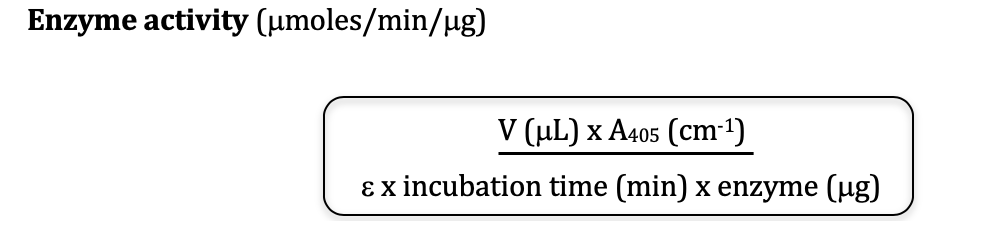How To Calculate Turnover Number Of Enzyme

In the intricate world of biochemistry, enzymes reign supreme, orchestrating reactions with unparalleled efficiency. Understanding their catalytic prowess is paramount, and the turnover number emerges as a crucial metric for quantifying this ability. However, the path to accurately determining this value isn't always straightforward, demanding careful consideration of experimental design and data analysis.

This article delves into the methods used to calculate the turnover number of an enzyme. We aim to provide a comprehensive guide, drawing from established biochemical principles and reputable scientific resources, for researchers and students alike.

Understanding the Turnover Number (k_cat)

The turnover number, often denoted as k_cat, represents the maximum number of substrate molecules that one enzyme molecule can convert into product per unit time when the enzyme is fully saturated with substrate. It's a direct measure of the enzyme's intrinsic catalytic activity.

A high turnover number signifies a highly efficient enzyme. Conversely, a low turnover number indicates a slower catalytic rate.

Essential Parameters for Calculation

Calculating the turnover number requires knowledge of several key parameters. These include the maximum reaction velocity (V_max) and the total enzyme concentration ([E]_T).

V_max represents the maximum rate of the enzyme-catalyzed reaction when the enzyme is saturated with substrate. [E]_T is the total concentration of enzyme present in the reaction mixture.

Determining V_max

The Michaelis-Menten equation forms the basis for determining V_max. This equation relates the initial reaction velocity (v₀) to the substrate concentration ([S]).

The Michaelis-Menten equation is: v₀ = (V_max[S]) / (K_M + [S]), where K_M is the Michaelis constant. V_max can be graphically determined from a plot of v₀ versus [S].

Graphical Methods

Plotting initial reaction velocities against varying substrate concentrations yields a hyperbolic curve. V_max is the asymptotic value that the curve approaches as the substrate concentration increases.

Lineweaver-Burk plots, also known as double-reciprocal plots, provide a linear representation of the Michaelis-Menten equation. This plot is generated by plotting 1/v₀ against 1/[S]. The y-intercept of the Lineweaver-Burk plot equals 1/V_max, allowing for easy determination of V_max.

Non-Linear Regression Analysis

Modern data analysis often employs non-linear regression techniques. Software packages can fit the Michaelis-Menten equation directly to experimental data, providing a more accurate estimate of V_max and K_M.

These methods minimize subjective interpretation and provide statistical measures of uncertainty, making them preferable to graphical methods.

Calculating Enzyme Concentration ([E]_T)

Accurately determining the total enzyme concentration is crucial. This can be achieved through various methods, including spectrophotometry and activity assays.

Spectrophotometry relies on the enzyme's absorbance properties at specific wavelengths. The Beer-Lambert Law relates absorbance to concentration, requiring knowledge of the enzyme's molar extinction coefficient.

Spectrophotometric Methods

The Beer-Lambert Law states: A = εbc, where A is the absorbance, ε is the molar extinction coefficient, b is the path length of the light beam through the sample, and c is the concentration.

By measuring the absorbance of a known sample and utilizing the molar extinction coefficient, the enzyme concentration can be calculated. Ensure the enzyme is pure for accurate spectrophotometric determination.

Active Site Titration

Active site titration offers a more direct measurement of the concentration of active enzyme molecules. This involves using a titrant that binds specifically and irreversibly to the enzyme's active site.

By monitoring the reaction until the enzyme is completely inhibited, the concentration of active sites can be determined. This method is particularly useful when dealing with enzyme preparations that may contain inactive enzyme molecules.

Calculating k_cat

Once V_max and [E]_T are determined, the turnover number can be calculated using the following equation: k_cat = V_max / [E]_T.

The units of k_cat are typically expressed as s^-1, representing the number of substrate molecules converted to product per enzyme molecule per second.

Example Calculation

Let's assume V_max is determined to be 10 μM/s and [E]_T is 0.1 μM. The turnover number would be: k_cat = 10 μM/s / 0.1 μM = 100 s^-1.

This indicates that each enzyme molecule can convert 100 substrate molecules into product every second under saturated conditions.

Factors Affecting Turnover Number

Several factors can influence the apparent turnover number. These include temperature, pH, and the presence of inhibitors or activators.

Optimal conditions are crucial for achieving accurate and meaningful k_cat values. Deviations from these conditions can lead to underestimation or overestimation of the true turnover number.

Importance of Proper Controls

Including appropriate controls in enzyme assays is paramount. Controls help to account for non-enzymatic reactions and ensure that the measured activity is solely due to the enzyme of interest.

Blank reactions, lacking either the enzyme or the substrate, are essential controls. Subtracting background rates from enzyme-catalyzed reaction rates provides a more accurate measure of enzyme activity.

Applications and Significance

The turnover number is a valuable parameter for comparing the catalytic efficiencies of different enzymes. It provides insights into the enzyme's mechanism of action and its role in biological processes.

Furthermore, k_cat is essential in drug discovery and development. Understanding the turnover number allows researchers to design inhibitors that effectively target enzymes involved in disease pathways.

Future Directions

Advancements in enzyme kinetics continue to refine the methods for determining turnover numbers. Microfluidic devices and high-throughput screening technologies enable rapid and precise measurement of enzyme activity.

These innovations promise to accelerate the discovery and characterization of novel enzymes. This will lead to a deeper understanding of biological processes and the development of new biotechnological applications.Therefore, accurately determining and applying turnover numbers is critical for future innovation and advancements.