How To Find The Volume Of A Composite Solid

Urgent alert: Many students are struggling with calculating the volume of complex shapes. Master this skill immediately to ace your next test and excel in real-world applications.
This guide provides a clear, concise method for determining the volume of composite solids, crucial for geometry, engineering, and architecture. Don't fall behind – understand this fundamental concept now.
Identifying Composite Solids
A composite solid is simply a three-dimensional shape made up of two or more simpler solids, such as cubes, prisms, cylinders, cones, and spheres. Recognizing these individual shapes is the first crucial step. Think of it as dissecting the object into its building blocks.
Examine the solid carefully. Look for distinct sections or boundaries that indicate different geometric forms.
The Addition Method: Combining Volumes
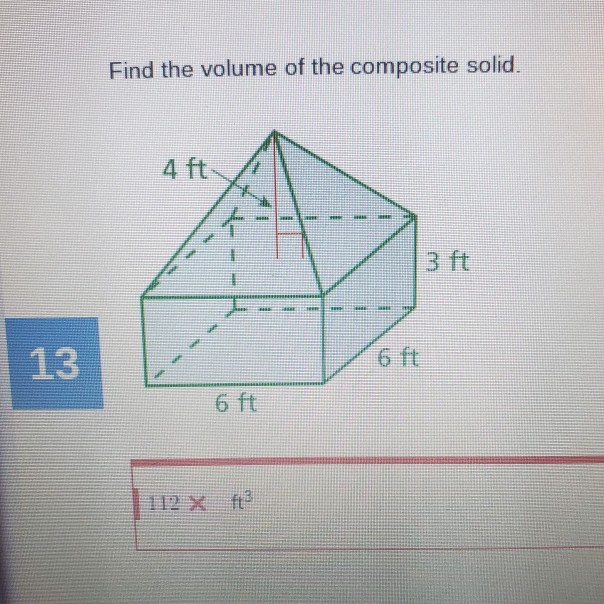
If the composite solid is formed by joining separate shapes, calculate the volume of each individual shape. Then, add these volumes together to get the total volume of the composite solid.
For example, imagine a solid made of a cube sitting on top of a rectangular prism. Calculate the volume of the cube. Then, calculate the volume of the prism. Finally, add the two volumes.
Volume Formulas: Quick Reference
Here are some essential volume formulas you'll need:
- Cube: V = s3 (where s is the side length)
- Rectangular Prism: V = lwh (where l is length, w is width, and h is height)
- Cylinder: V = πr2h (where r is the radius and h is height)
- Cone: V = (1/3)πr2h (where r is the radius and h is height)
- Sphere: V = (4/3)πr3 (where r is the radius)
The Subtraction Method: Removing Volumes
Sometimes, a composite solid is formed by removing a shape from a larger shape. In this case, you'll need to use the subtraction method.
Calculate the volume of the larger shape. Then, calculate the volume of the shape that was removed. Subtract the volume of the removed shape from the volume of the larger shape. This will give you the volume of the composite solid.
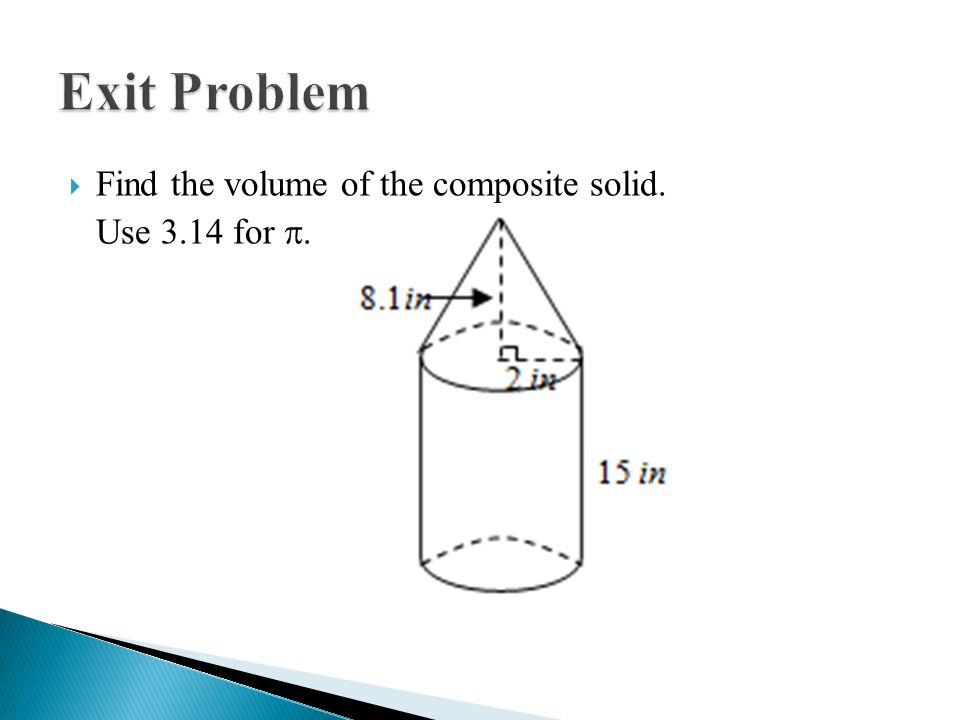
Consider a cylinder with a cone-shaped hole drilled through the center. Find the cylinder's volume. Find the cone's volume. Subtract the cone's volume from the cylinder's volume.
Complex Examples: A Step-by-Step Approach
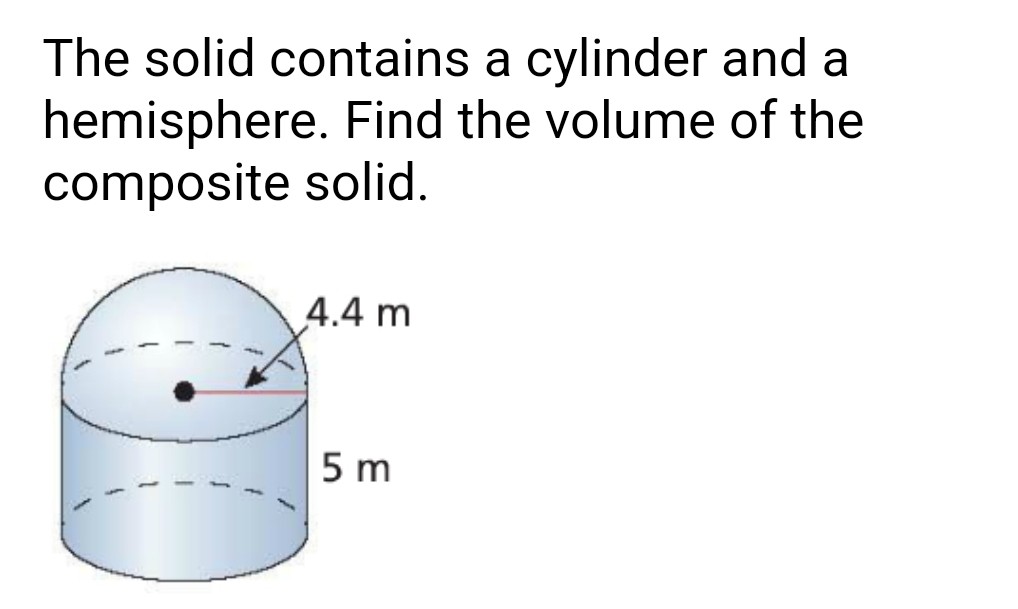
Let's break down a more challenging example: a hemisphere sitting on top of a cylinder. First, find the radius (r) which will be same for the hemisphere and the cylinder.
Calculate the volume of the hemisphere: V = (1/2) * (4/3)πr3 = (2/3)πr3. Then, calculate the volume of the cylinder: V = πr2h. Finally, add the two volumes together: Vtotal = (2/3)πr3 + πr2h.
Dealing with Overlapping Regions
Be extremely careful when dealing with solids that might have overlapping regions. If shapes overlap, ensure you don't count the overlapping volume twice. This often involves carefully visualizing and dissecting the solid.
For example, if two cubes are glued together face-to-face, the volume of the glue face isn't added. This seems obvious, but complex geometries can make it hard to visualize.
Real-World Applications: Why This Matters
Calculating the volume of composite solids is essential in many fields. Architects use it to determine the amount of material needed for construction. Engineers use it in designing everything from bridges to airplanes.
Even everyday tasks, like determining how much water a uniquely shaped vase can hold, rely on this skill. It's not just about math class; it's a practical skill for problem-solving.
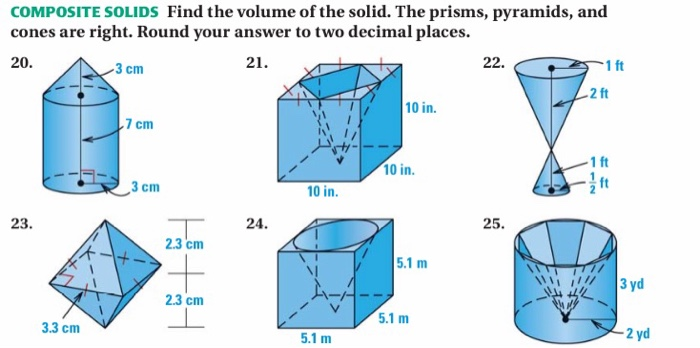
Practice Problems: Sharpen Your Skills
Practice is key to mastering this concept. Work through a variety of examples, starting with simple shapes and gradually increasing the complexity.
Use online resources, textbooks, and worksheets to find practice problems. Don't be afraid to ask for help from teachers or classmates.
Conclusion: Immediate Action Required
Understanding how to calculate the volume of composite solids is a critical skill for success in math and beyond. Don't delay: review the formulas, practice the methods, and master this essential concept.
Ongoing research into advanced geometric principles continues to refine our understanding of volume calculations. Stay updated on new developments to stay ahead.