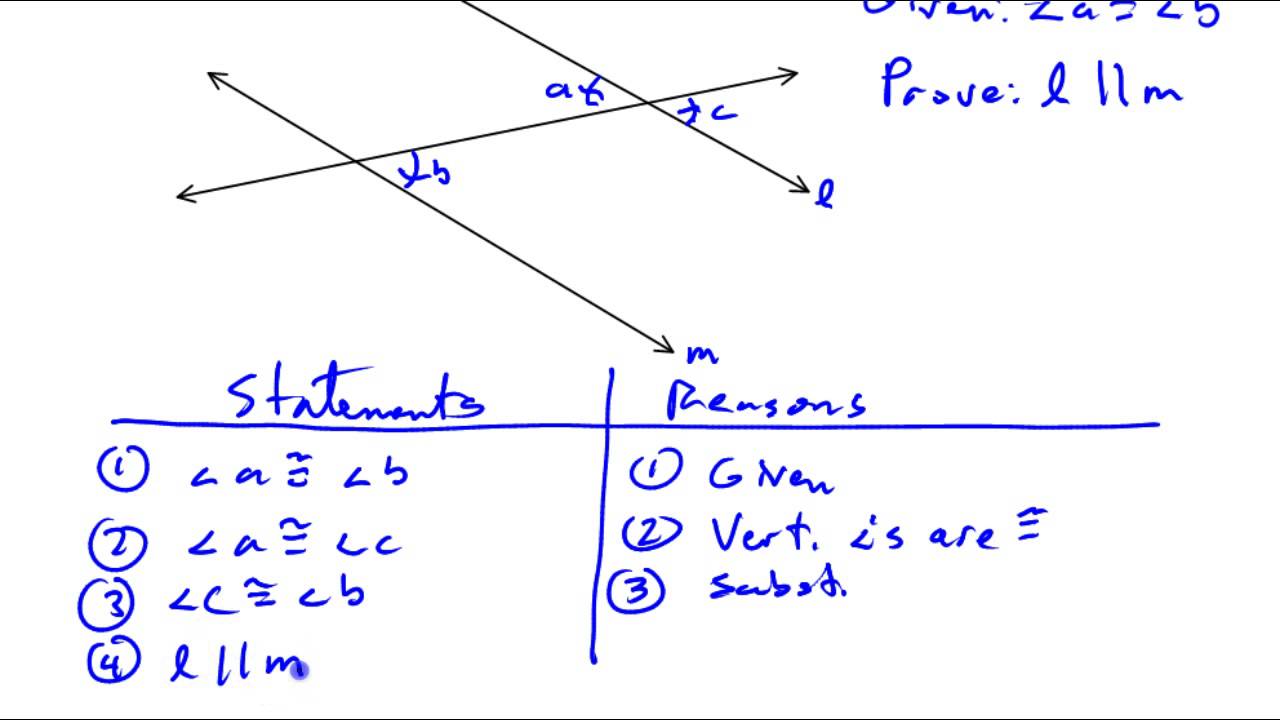
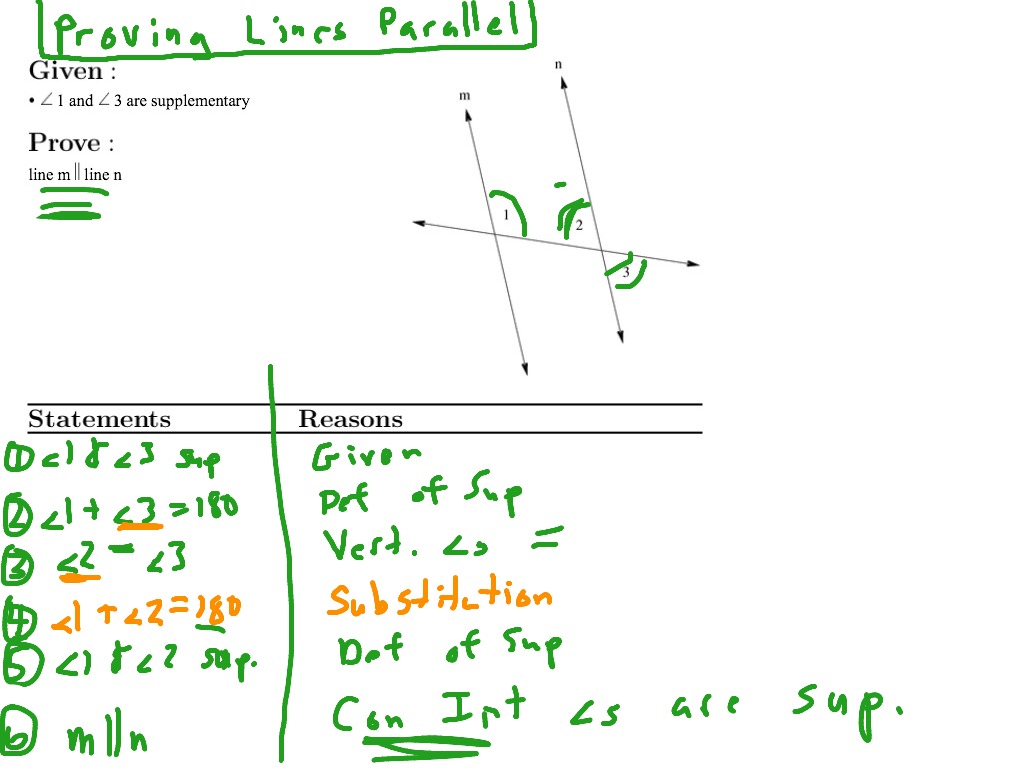
How To Prove A Line Is Parallel
Imagine a world without parallel lines. Picture buildings tilting precariously, bridges collapsing into rivers, and maps resembling abstract art more than accurate representations of reality. The simple concept of parallel lines, those unwavering paths that never meet, underpins so much of our structured world, from the architecture we inhabit to the very fabric of geometry.
At its core, understanding how to prove that lines are parallel is fundamental not just to mathematics, but to logical reasoning and problem-solving skills applicable across numerous disciplines. This article demystifies the methods of proving parallelism, breaking down the geometric principles involved and showing how they connect to real-world applications.
Parallel lines, by definition, are lines in the same plane that never intersect. But stating this definition is not enough to prove that two lines are actually parallel. To do so, we rely on geometric postulates, theorems, and angle relationships formed when a transversal – a line that intersects two or more other lines – cuts through them.
The Foundation: Angle Relationships and Transversals
The entire edifice of parallel line proofs rests upon understanding the angles formed when a transversal intersects two lines. These angles have special names and relationships that are crucial for establishing parallelism.
Corresponding Angles
Corresponding angles occupy the same relative position at each intersection. Think of them as being in the "same corner".
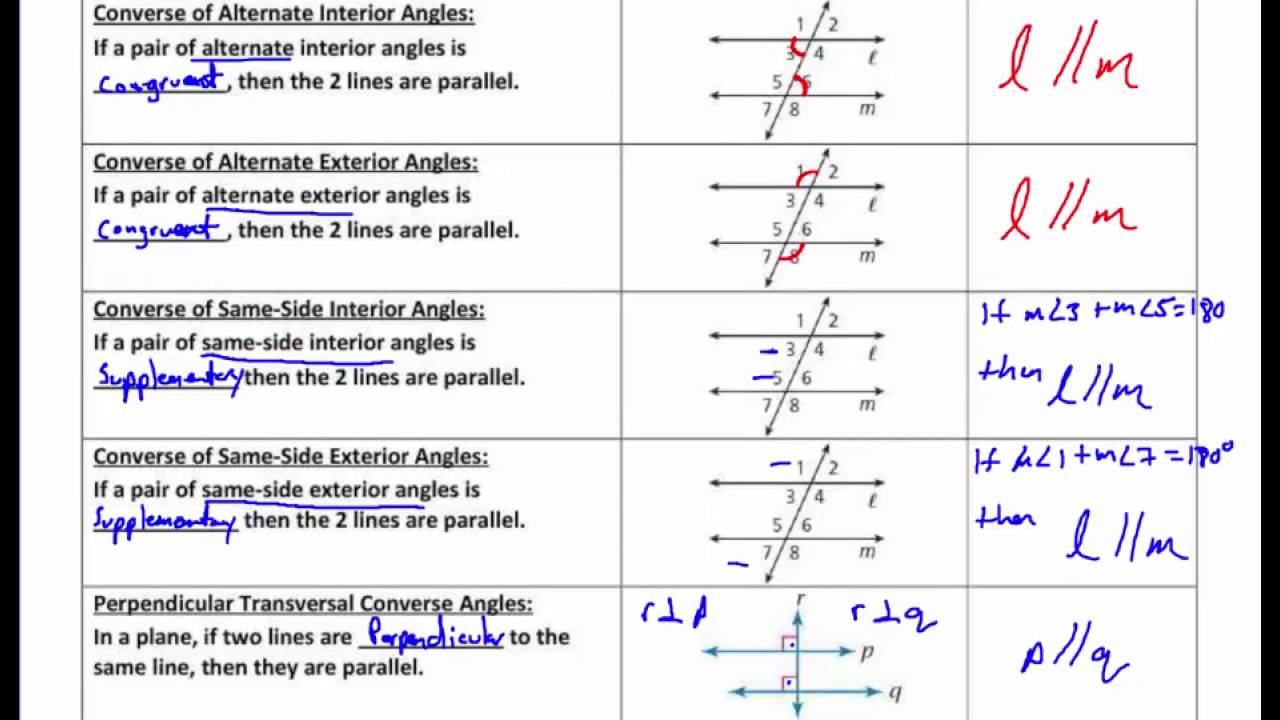
If corresponding angles are congruent (equal in measure), then the lines are parallel. This is known as the Corresponding Angles Postulate.
Alternate Interior Angles
Alternate interior angles lie on opposite sides of the transversal and between the two lines. Imagine them as being tucked inside the space between the two lines but on different sides of the transversal.
The Alternate Interior Angles Theorem states that if alternate interior angles are congruent, then the lines are parallel. Conversely, if the lines are parallel, then the alternate interior angles are congruent.
Alternate Exterior Angles
Alternate exterior angles lie on opposite sides of the transversal and outside the two lines. They are the exterior counterparts to the alternate interior angles.
Similarly, the Alternate Exterior Angles Theorem states that if alternate exterior angles are congruent, then the lines are parallel, and vice versa.
Consecutive Interior Angles (Same-Side Interior Angles)
Consecutive interior angles, also known as same-side interior angles, lie on the same side of the transversal and between the two lines. They are nestled inside the space between the two lines on the same side of the transversal.
The Consecutive Interior Angles Theorem states that if consecutive interior angles are supplementary (add up to 180 degrees), then the lines are parallel. And, of course, if the lines are parallel, the consecutive interior angles are supplementary.
Methods for Proving Parallel Lines
Now, let's put this knowledge into practice. Here's a breakdown of the key methods used to prove that two lines are parallel, each rooted in the angle relationships described above.
Method 1: Using the Corresponding Angles Postulate
Identify a transversal cutting through the two lines you want to prove are parallel. Measure (or be given) the measures of a pair of corresponding angles.
If the corresponding angles are congruent, then you can definitively state that the lines are parallel based on the Corresponding Angles Postulate.
Method 2: Using the Alternate Interior Angles Theorem
As before, locate a transversal and a pair of alternate interior angles. Determine if these angles are congruent.
If they are, the Alternate Interior Angles Theorem immediately proves that the lines are parallel.
Method 3: Using the Alternate Exterior Angles Theorem
This method mirrors the previous one but focuses on alternate exterior angles. If you can establish that a pair of alternate exterior angles are congruent, then the lines are parallel thanks to the Alternate Exterior Angles Theorem.
Method 4: Using the Consecutive Interior Angles Theorem
In this approach, focus on consecutive interior angles. Measure or determine the measures of these angles.
If the sum of their measures is 180 degrees (supplementary), then the Consecutive Interior Angles Theorem confirms that the lines are parallel.
Method 5: Lines Perpendicular to the Same Line
This is a less direct but powerful method. If two lines are each perpendicular to the same line, then those two lines are parallel to each other.
This is because perpendicular lines form right angles (90 degrees), and if both lines create right angles with the same transversal, the corresponding angles are congruent.
Method 6: Transitive Property of Parallel Lines
This method relies on a chain reaction of parallelism. If line 'a' is parallel to line 'b', and line 'b' is parallel to line 'c', then line 'a' is also parallel to line 'c'.
This transitive property allows you to establish parallelism indirectly by linking lines through a common parallel intermediary.
Real-World Applications and Significance
The seemingly abstract concept of parallel lines has profound real-world applications. Consider architecture: buildings rely on parallel lines for structural integrity and aesthetic appeal.
Bridges, roads, and railway tracks depend on parallelism for safety and efficient functionality. Urban planning utilizes parallel lines to create organized and navigable cityscapes.
Even in art and design, the principles of parallel lines are used to create perspective, depth, and visual harmony. They are fundamental building blocks in many creative fields.
Beyond Geometry: Cultivating Logical Thinking
The process of proving lines are parallel isn't merely about memorizing theorems and applying formulas. It's an exercise in logical deduction and critical thinking.
Learning to construct a rigorous proof, to identify relevant information, and to apply geometric principles is a valuable skill that extends far beyond the realm of mathematics.
These skills are transferable to problem-solving in any field, from scientific research to business strategy to everyday decision-making.
By mastering the art of proving parallel lines, we are not just learning about geometry; we are honing our ability to think clearly, reason logically, and approach challenges with a structured and analytical mindset.
So, the next time you encounter parallel lines, remember that they represent more than just a geometric concept. They are a testament to the power of logical reasoning and a reminder of the underlying order that shapes our world.