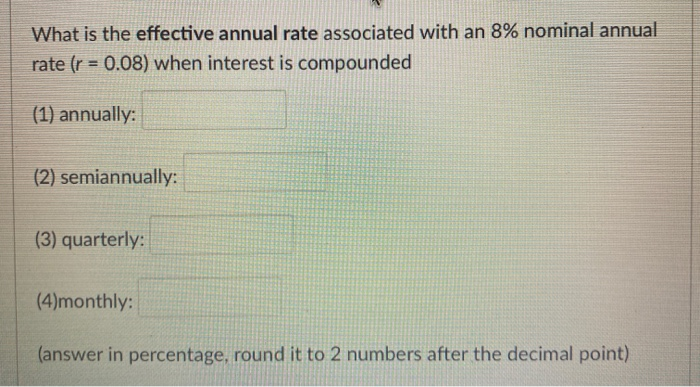
Identify A True Statement About The Effective Annual Rate
The effective annual rate (EAR), a crucial metric in financial planning and investment analysis, has been the subject of ongoing discussion among financial professionals and consumers alike. Understanding its true nature is essential for making informed financial decisions, whether it's choosing a savings account, evaluating a loan, or comparing investment opportunities.
At its core, the EAR provides a standardized measure of the actual interest earned or paid on an investment or loan over a one-year period. The key is that it takes into account the effect of compounding, unlike the stated or nominal interest rate. This distinction is critical for accurate financial comparisons.
Understanding the Effective Annual Rate
The EAR, sometimes also referred to as the annual equivalent rate (AER), is a more accurate reflection of the true cost of borrowing or the true return on an investment. This is especially the case when interest is compounded more frequently than annually.
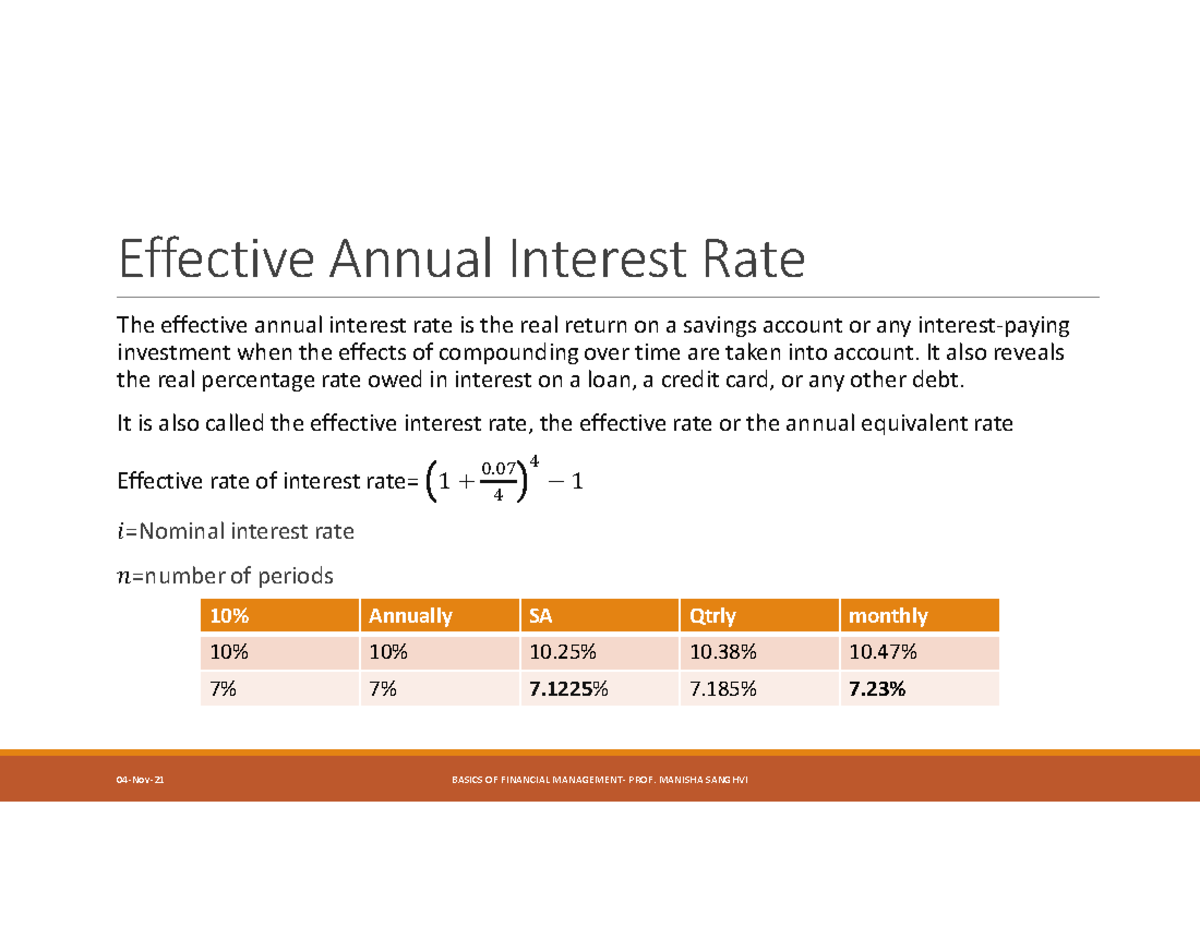
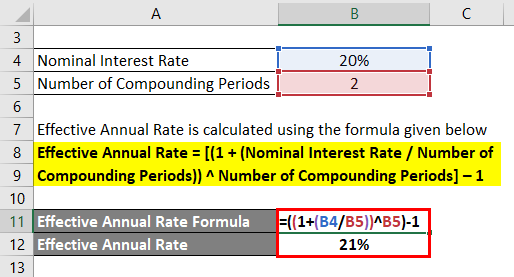
The formula for calculating the EAR is: EAR = (1 + (i/n))^n - 1, where i represents the stated annual interest rate and n represents the number of compounding periods per year. This calculation highlights the impact of compounding on the overall return.
The True Statement: Compounding Matters
A true statement about the effective annual rate is that it always equals the nominal or stated interest rate when interest is compounded annually. When compounding happens more frequently than annually (e.g., monthly, daily), the EAR will be higher than the stated annual interest rate.
This occurs because the interest earned in each compounding period is added to the principal, and then earns interest itself in subsequent periods. The more frequently interest is compounded, the greater the impact on the EAR.
Consider two investment options: one offering a 5% stated annual interest rate compounded annually, and another offering the same 5% stated rate but compounded monthly. In the first case, the EAR is also 5%. In the second, the EAR will be slightly higher than 5% due to the monthly compounding effect.
Significance for Consumers
The EAR is a vital tool for consumers comparing financial products. It provides a consistent and transparent way to evaluate different loan offers, credit card rates, and investment options. By focusing on the EAR, consumers can avoid being misled by lower stated interest rates that fail to account for frequent compounding.
For example, when evaluating credit card offers, it’s important to look beyond the annual percentage rate (APR), which is the stated interest rate. A credit card with a seemingly low APR but daily compounding may actually have a higher EAR than a card with a slightly higher APR but less frequent compounding.
Similarly, when choosing a savings account, understanding the EAR allows consumers to identify the account that will provide the highest return on their savings. Banks and credit unions are required to disclose the EAR so consumers can compare effectively.
Implications for Businesses and Investors
Businesses use the EAR to evaluate the true cost of borrowing money and the potential return on investments. Accurate EAR calculations are essential for effective financial planning and risk management.
Investors rely on the EAR to compare investment opportunities with different compounding frequencies. It provides a standardized measure of return that facilitates informed decision-making.
By understanding and utilizing the EAR, businesses can optimize their financial strategies and ensure they are making the most advantageous borrowing and investment choices.
Expert Perspectives
According to Dr. Anya Sharma, a professor of finance at the University of Metropolitan City, "The EAR is a fundamental concept in finance that should be understood by everyone. It empowers individuals and businesses to make informed financial decisions by providing a clear and accurate picture of the true cost of borrowing and the true return on investment."
She further explains, "Ignoring the impact of compounding can lead to significant miscalculations and potentially costly mistakes. Always compare the EAR when evaluating financial products."
Conclusion
In conclusion, understanding the effective annual rate and its relationship to compounding is crucial for making sound financial decisions. The EAR provides a transparent and standardized measure of the true cost of borrowing and the true return on investment, empowering consumers, businesses, and investors alike.
Remember, if interest is compounded annually, the EAR equals the stated annual interest rate. If interest is compounded more frequently, the EAR will be higher, reflecting the impact of compounding.
