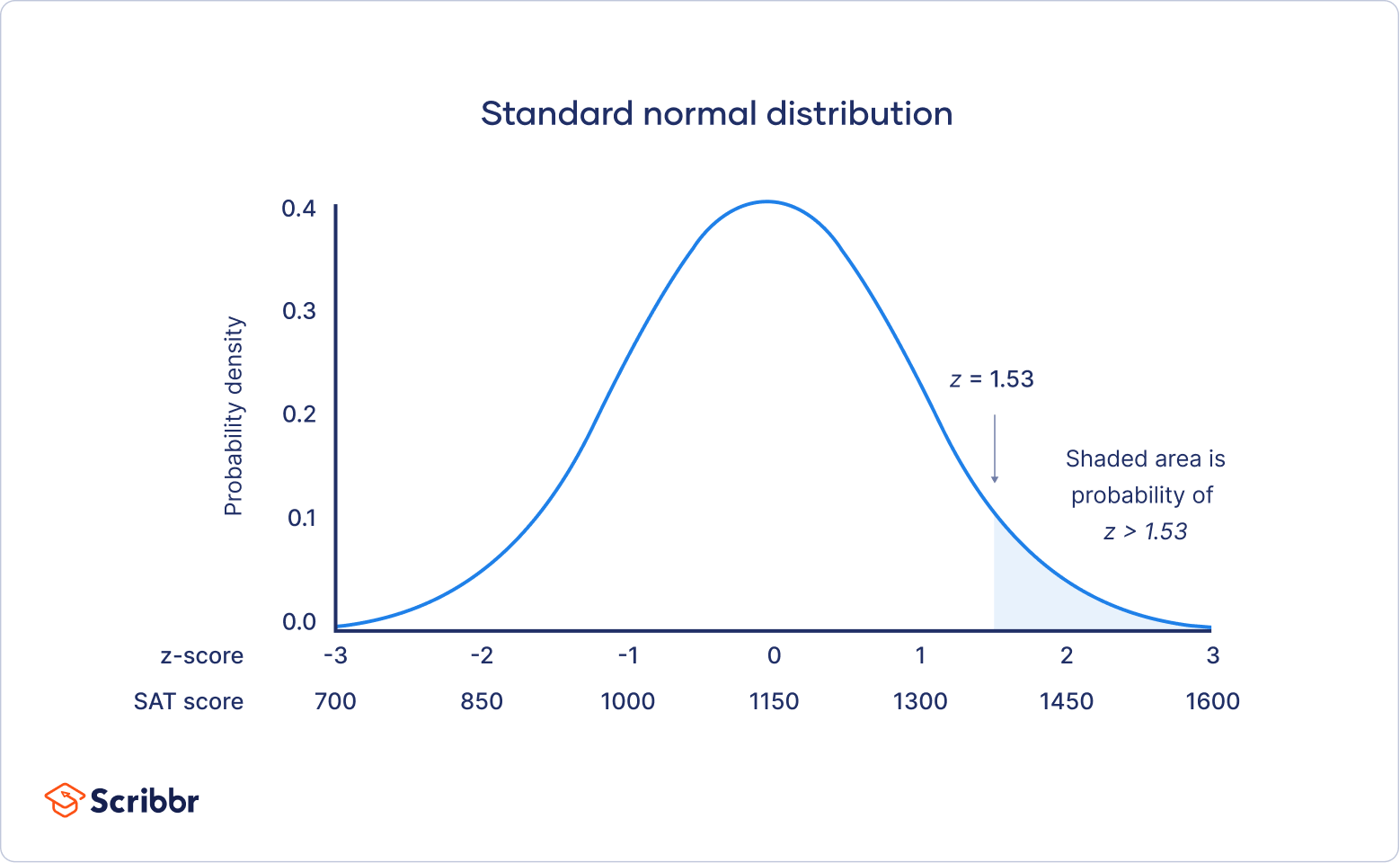
In Its Standardized Form The Normal Distribution

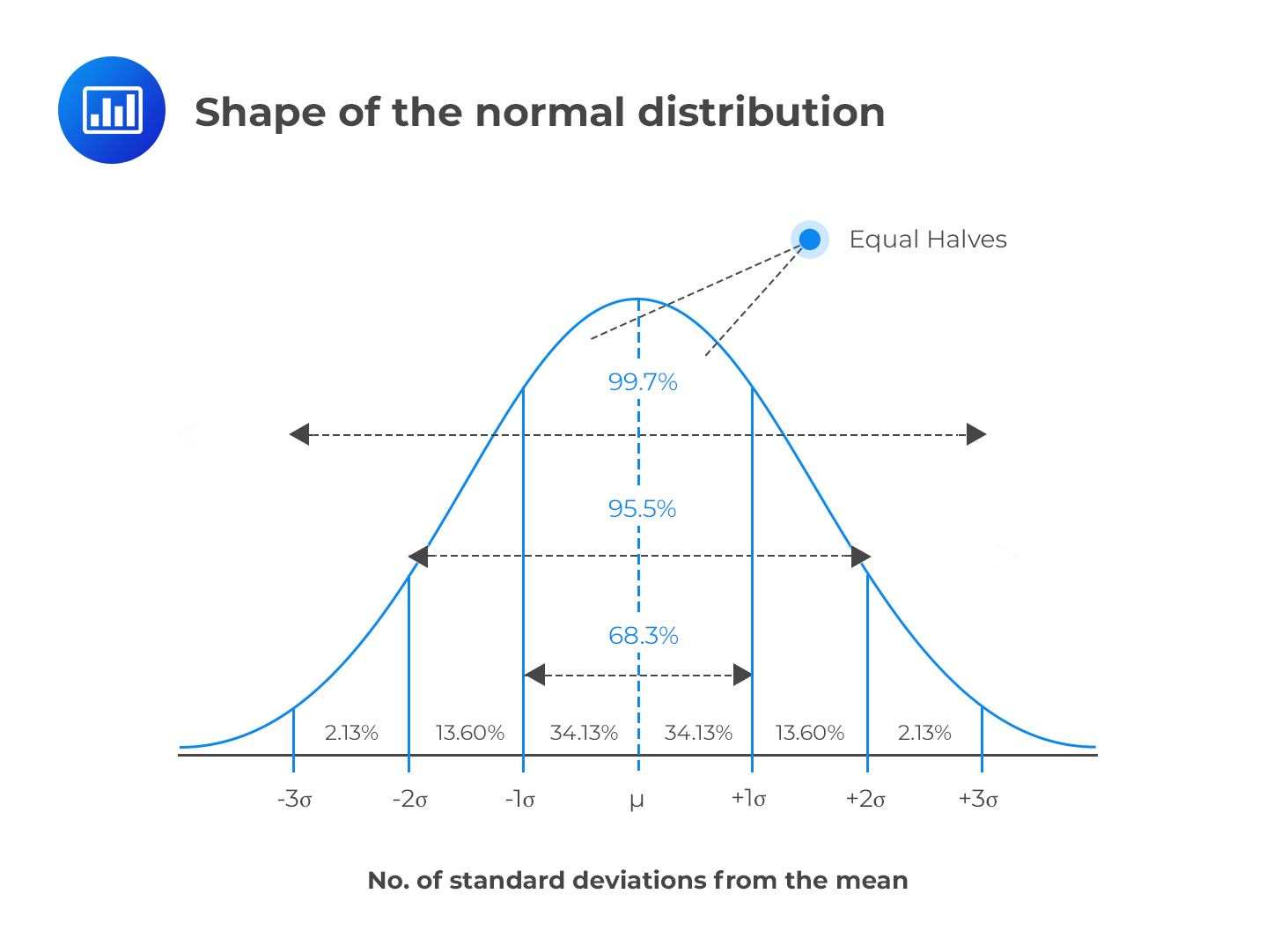
Imagine a gentle hill, perfectly symmetrical, rising to a single, majestic peak. Sunlight bathes its smooth slopes, casting soft shadows that emphasize its elegant curve. This isn't just any hill; it's a visual representation of one of the most fundamental concepts in statistics: the normal distribution, a pattern that quietly governs much of the world around us.

At its core, the normal distribution, also known as the Gaussian distribution or the bell curve, is a probability distribution that describes how data is distributed around its mean. This seemingly simple curve underpins a vast array of scientific and mathematical disciplines, from predicting election outcomes to designing effective medications. Understanding the normal distribution offers a powerful lens through which to interpret the world and make informed decisions based on data.

A Ubiquitous Pattern

The story of the normal distribution begins centuries ago, with mathematicians grappling with the intricacies of probability and error. Abraham de Moivre, a French mathematician, first discovered the shape in the 18th century while studying games of chance.

He realized that the distribution of outcomes tended to cluster around a central value. This work laid the groundwork for what would later become the formal definition of the normal distribution.

The Contributions of Gauss and Laplace

It was Carl Friedrich Gauss, however, who truly cemented the distribution's place in statistical history. He applied it to astronomy, using it to analyze errors in astronomical observations.

Independently, Pierre-Simon Laplace also explored the distribution, recognizing its importance in analyzing data from various fields. Their combined work led to the distribution being frequently referred to as the Gaussian distribution.

The Central Limit Theorem is a cornerstone of statistics, explaining why the normal distribution appears so frequently. It states that the sum of many independent, identically distributed random variables will tend to a normal distribution, regardless of the original distribution of those variables.

Think of flipping a coin. Each flip is independent, and the outcome is either heads or tails. But if you flip the coin many times and count the number of heads, the distribution of those counts will start to resemble a bell curve.

The Properties of the Bell Curve

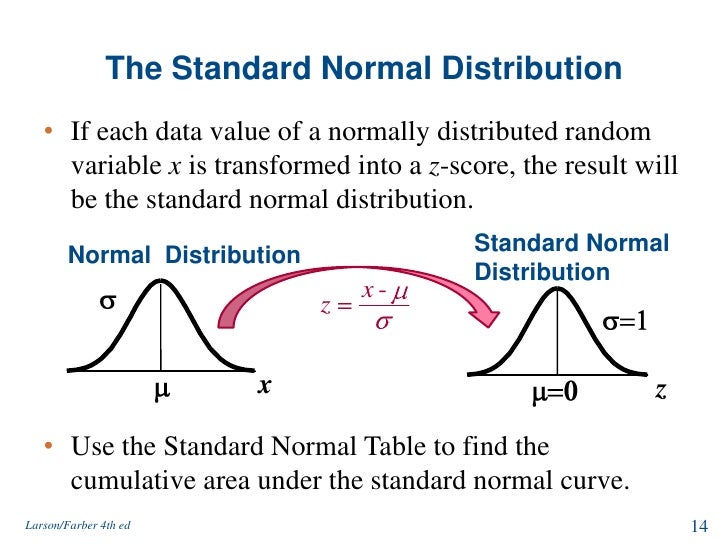
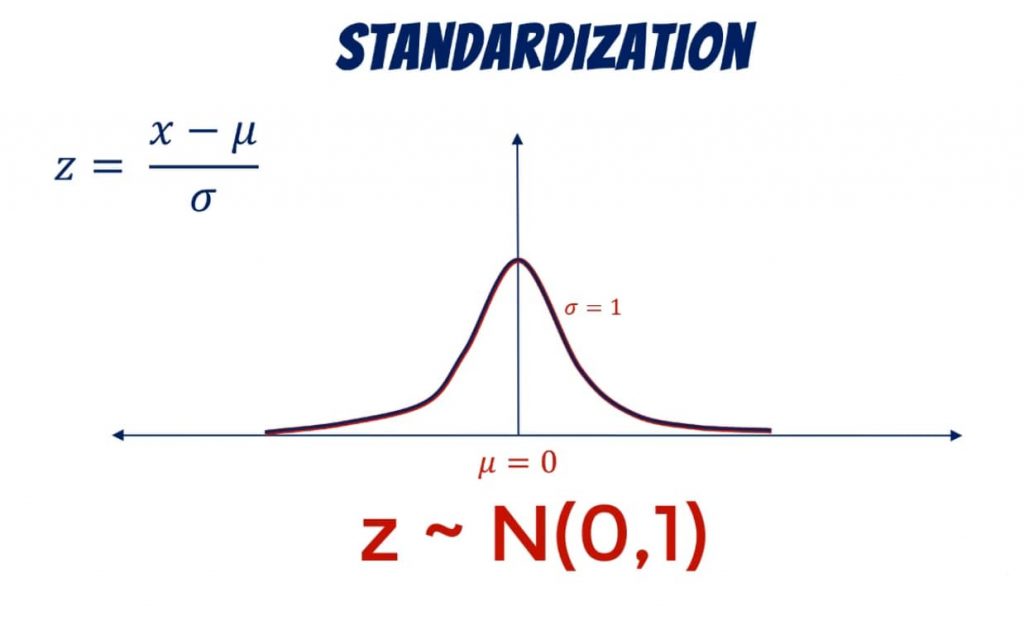
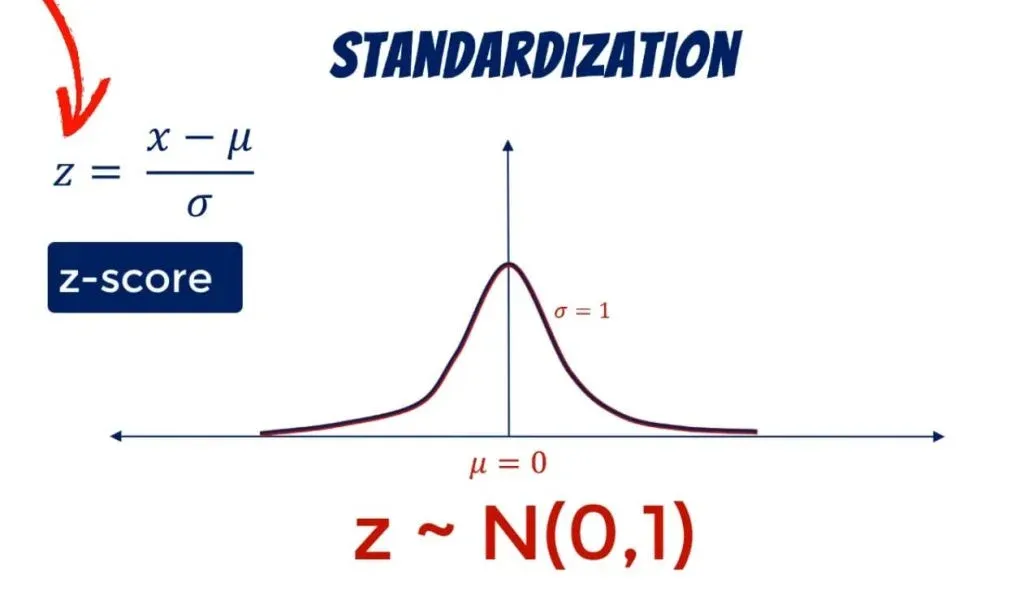
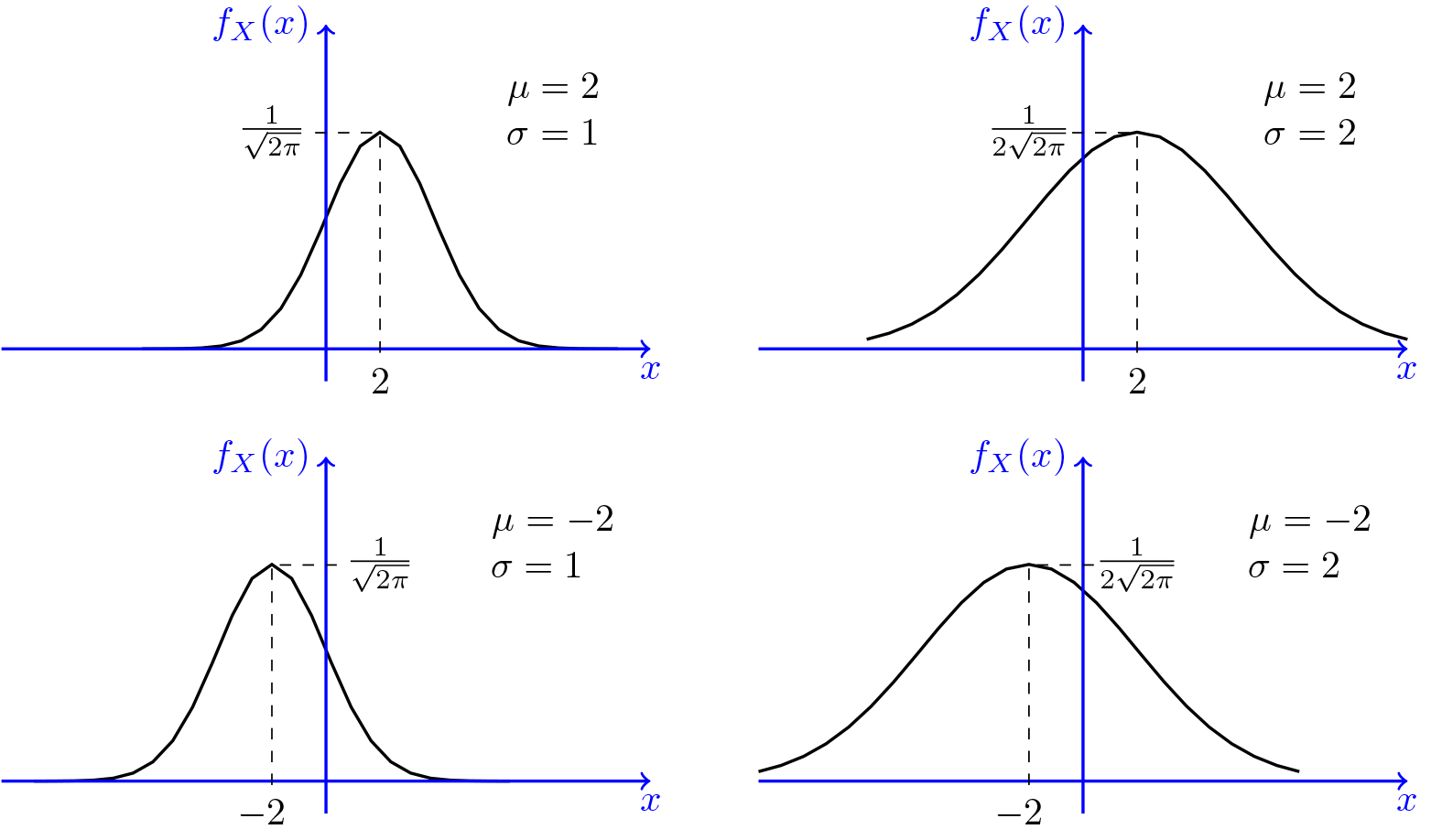
The beauty of the normal distribution lies in its simplicity and its well-defined properties. It's completely described by just two parameters: the mean and the standard deviation.

The mean represents the average value of the data, the central point around which the distribution is centered. The standard deviation measures the spread or dispersion of the data, indicating how tightly clustered the data points are around the mean.

A small standard deviation indicates that the data is closely concentrated around the mean, resulting in a tall, narrow bell curve. A large standard deviation suggests that the data is more spread out, creating a wider, flatter curve.

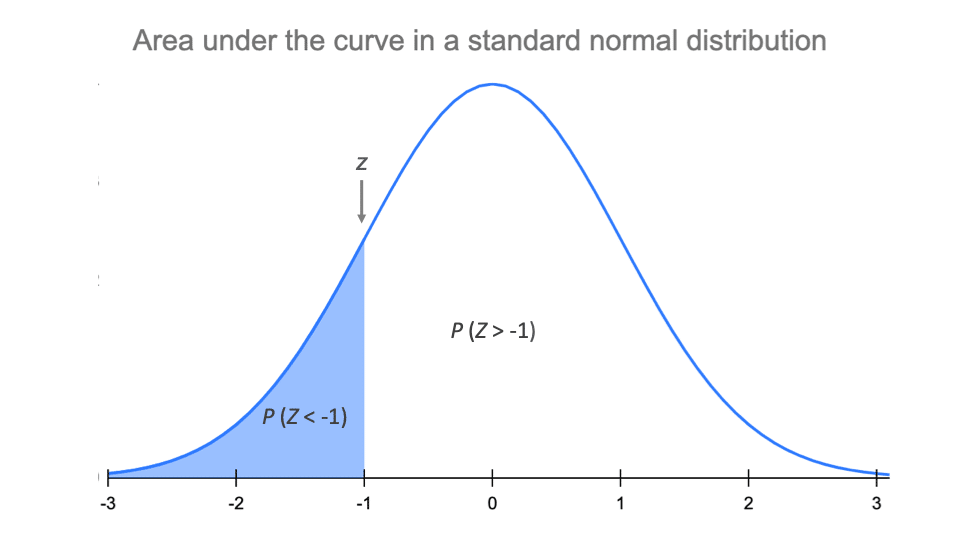
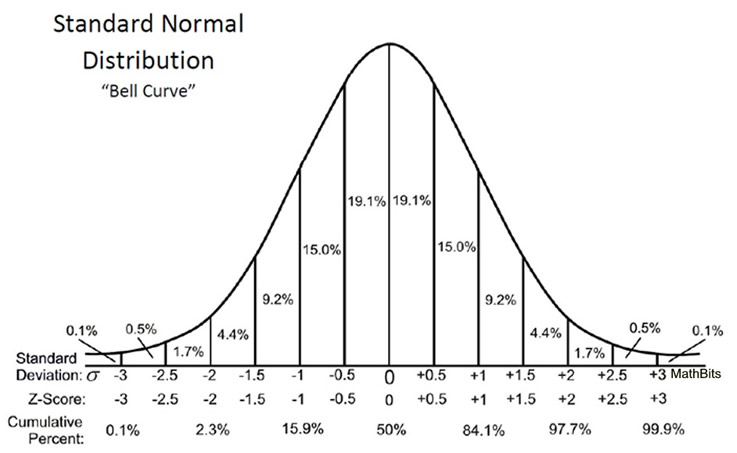
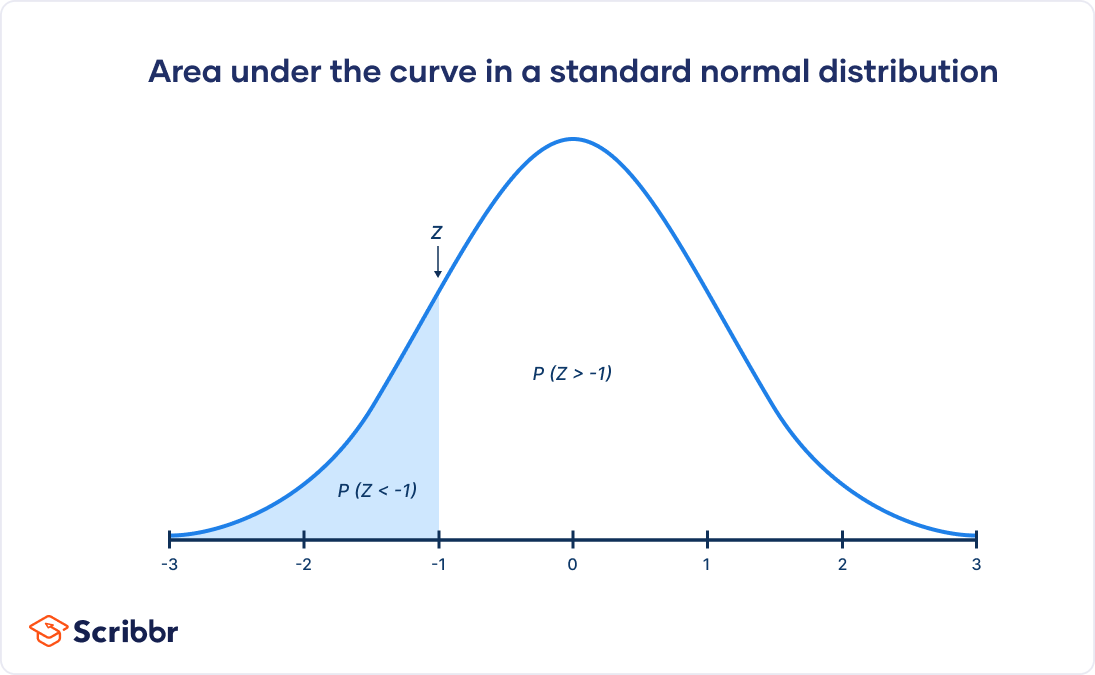
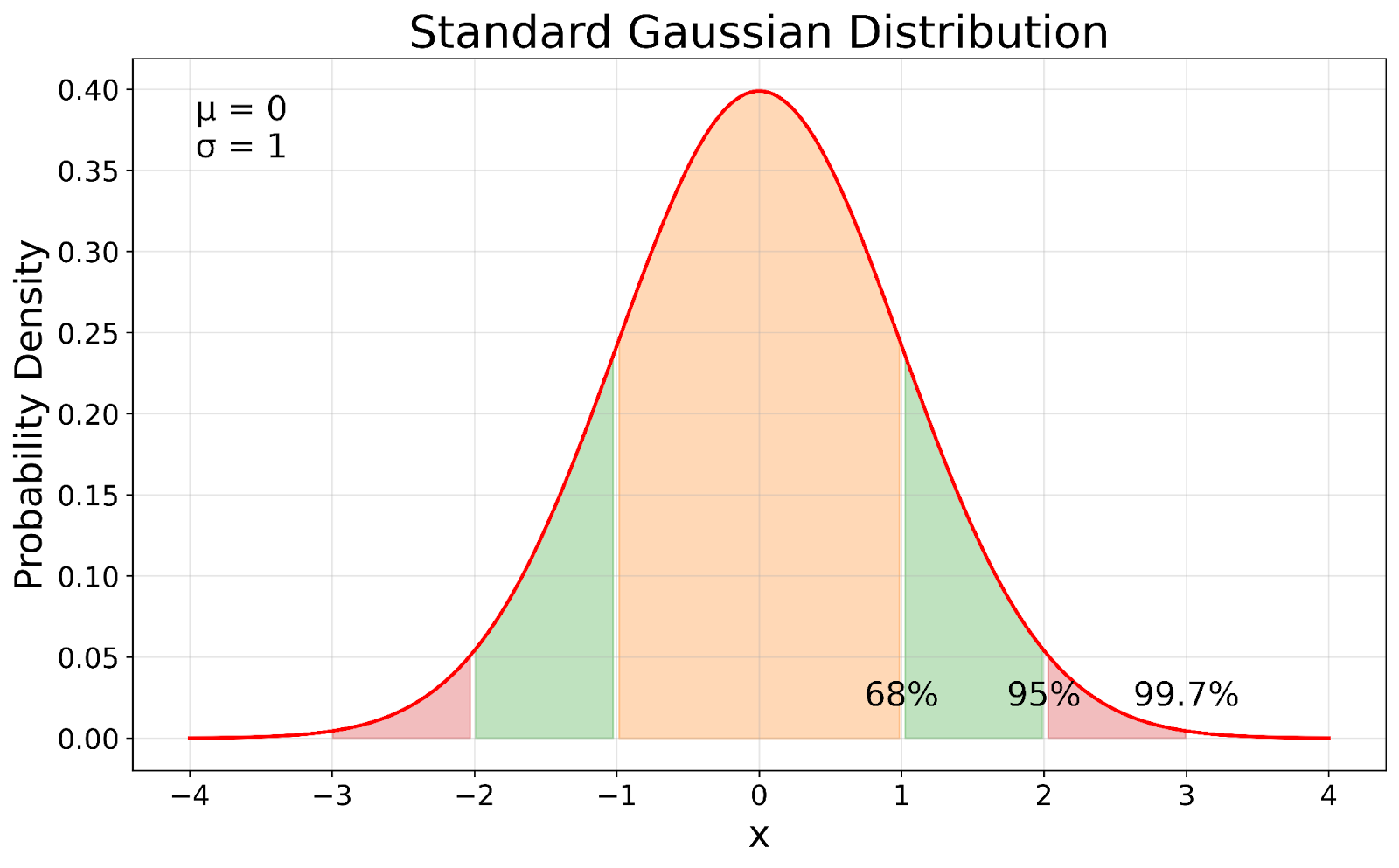
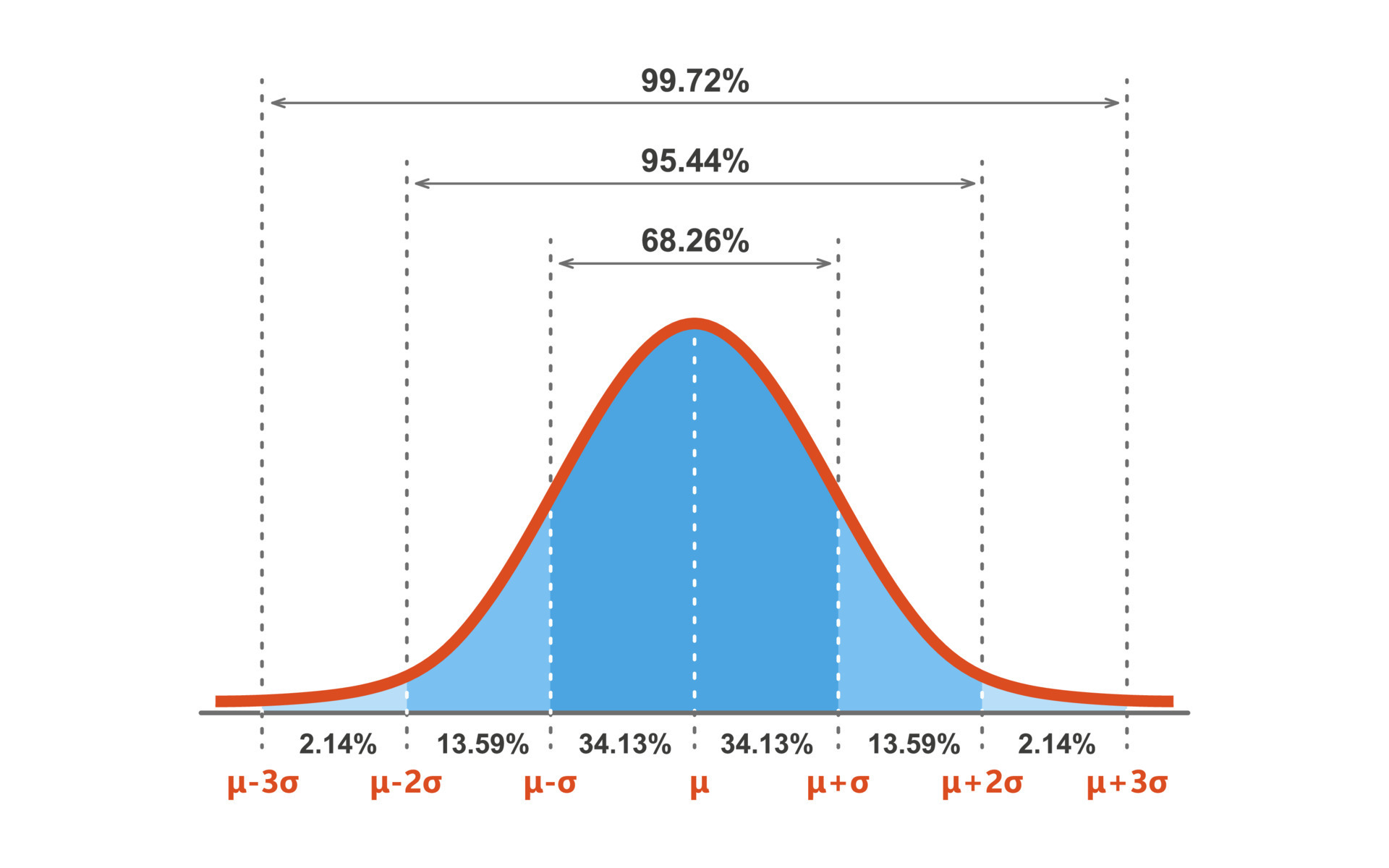
One of the most useful characteristics of the normal distribution is the 68-95-99.7 rule, also known as the empirical rule. This rule states that approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.

This rule allows us to quickly assess the likelihood of observing particular values in a normally distributed dataset. For example, if we know the mean height of adult women is 5'4" with a standard deviation of 2.5 inches, we can estimate that about 95% of women will be between 4'11" and 5'9".

Applications Across Disciplines

The normal distribution's versatility has made it an indispensable tool in countless fields. In healthcare, it's used to analyze patient data, such as blood pressure and cholesterol levels, to identify outliers and potential health risks.

In finance, it helps to model stock prices and investment returns, allowing analysts to assess risk and make informed investment decisions. Engineering relies on the normal distribution for quality control, ensuring that manufactured products meet specific standards and tolerances.

Social sciences use it to analyze survey data and understand population characteristics.

"The applications are virtually limitless," says Dr. Anya Sharma, a professor of statistics at the University of California, Berkeley. "Anywhere you have large datasets with random variation, the normal distribution is likely to be relevant."

Even in seemingly unrelated fields like sports, the normal distribution can provide valuable insights. Consider the distribution of marathon finishing times. While not perfectly normal due to factors like training and experience, the distribution often approximates a bell curve, allowing analysts to understand the typical range of finishing times and identify exceptional performances.

Beyond Perfection: Departures from Normality

While the normal distribution is a powerful tool, it's important to remember that it's a mathematical model, an idealization of reality. Not all datasets perfectly follow a normal distribution. Sometimes, data may be skewed, with more values concentrated on one side of the mean than the other.

Other times, the distribution may have heavier tails than a normal distribution, meaning that extreme values occur more frequently than predicted. These departures from normality don't invalidate the concept; they simply require more nuanced analysis and potentially the use of different statistical models.

Statisticians have developed various techniques to assess the normality of data, including graphical methods like histograms and Q-Q plots, as well as statistical tests like the Shapiro-Wilk test. These tools help researchers determine whether the normal distribution is a suitable model for their data and, if not, identify alternative distributions that may be more appropriate.

A Lasting Legacy

The normal distribution stands as a testament to the power of mathematical abstraction and its ability to illuminate the patterns that govern our world. From its humble beginnings in the study of games of chance to its widespread use in modern science and technology, it has proven to be an invaluable tool for understanding and interpreting data.

As we continue to generate and analyze ever-increasing amounts of data, the normal distribution will undoubtedly remain a central concept in statistical thinking, providing a framework for making sense of complexity and drawing meaningful conclusions from the information around us.

So, the next time you see a bell curve, remember that it's more than just a shape on a graph. It's a window into the underlying patterns of the universe, a reminder that even in the midst of chaos, there is often a beautiful order to be found.