Is 53 A Composite Or Prime Number
Imagine a cozy evening, the scent of cinnamon fills the air, and a group of friends huddles around a table, a chalkboard covered in numbers sits in the center. A spirited debate is underway: is 53 a composite number or a prime number? The question hangs in the air, thicker than the steam rising from their mugs of hot chocolate. It seems like a simple question, yet it invites a deeper dive into the fascinating world of numbers.
At its core, the debate centers around understanding the fundamental properties of numbers. Is 53 divisible only by 1 and itself, making it a prime number? Or does it have other factors, classifying it as a composite number? This seemingly basic question reveals a lot about number theory and its application.
Prime Numbers: The Building Blocks of Numbers
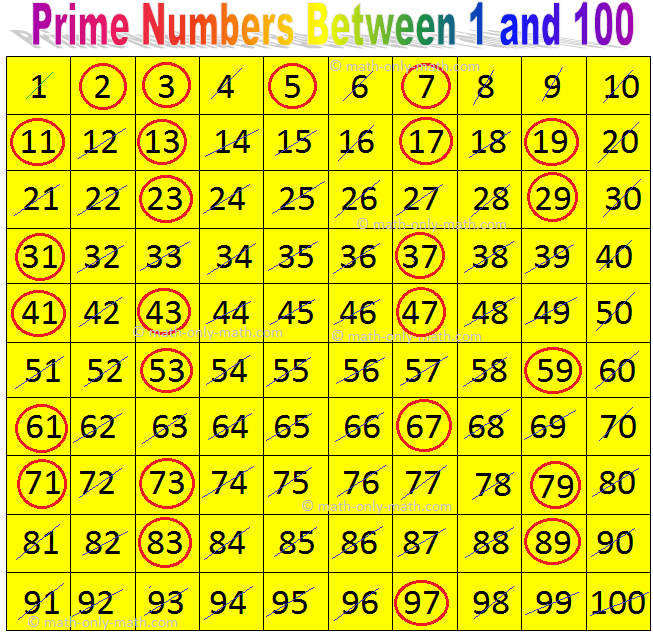
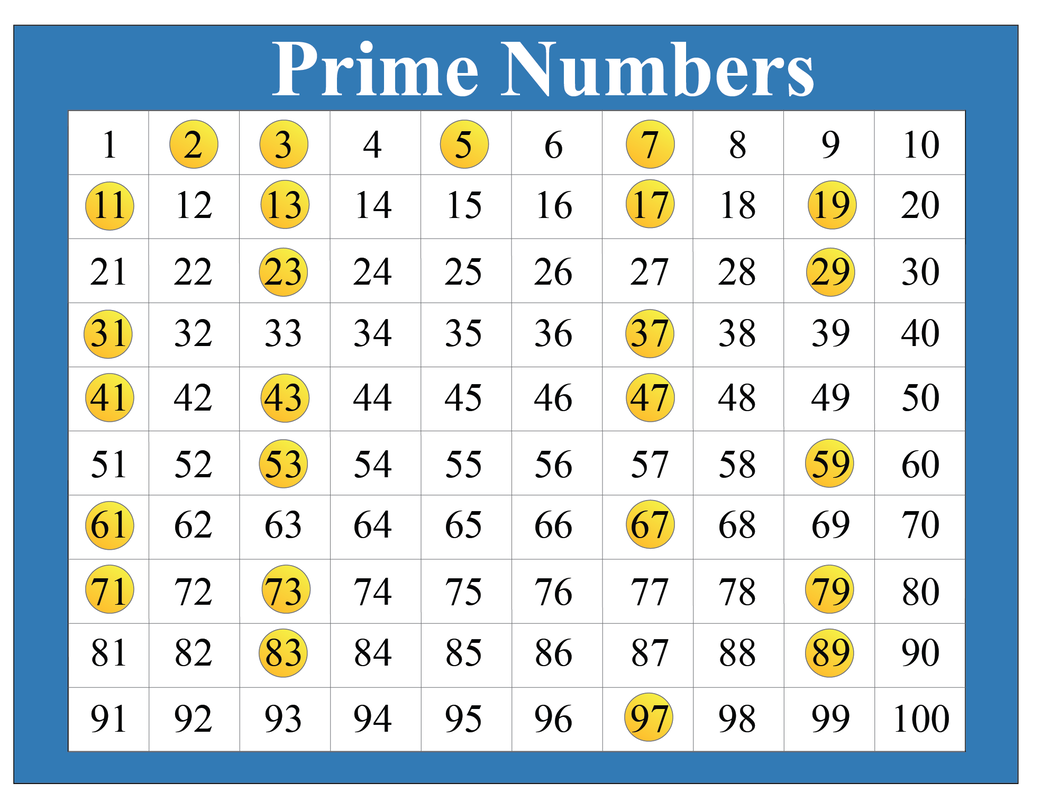
To understand the debate, let's start with the basics. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Think of 2, 3, 5, 7, and 11 – they are all exclusively divisible by 1 and themselves.
Prime numbers are the atoms of the number world, the fundamental building blocks from which all other numbers are constructed. They are infinitely many and follow no easily predictable pattern. This makes them fascinating for mathematicians and crucial in fields like cryptography.
The Sieve of Eratosthenes
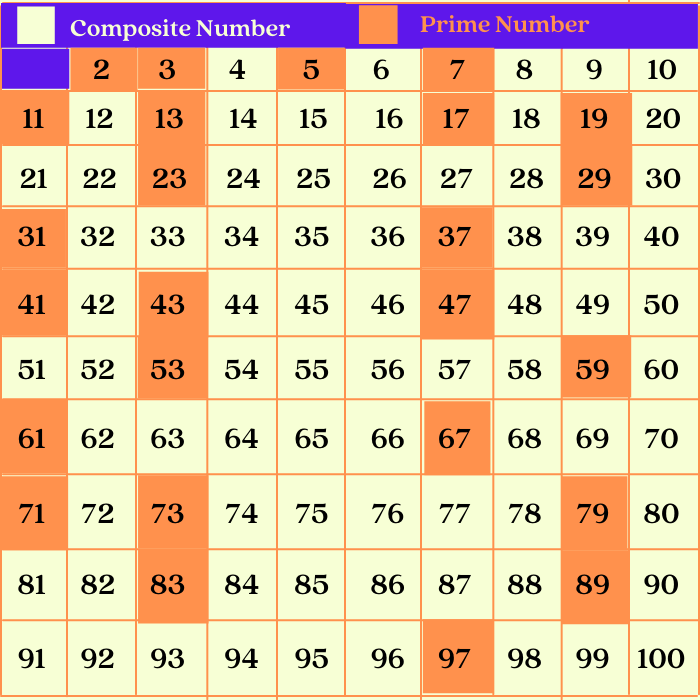
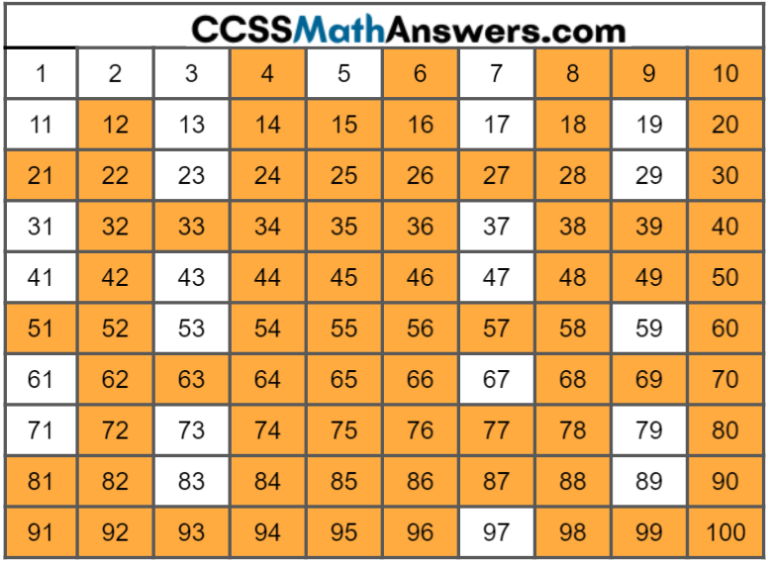
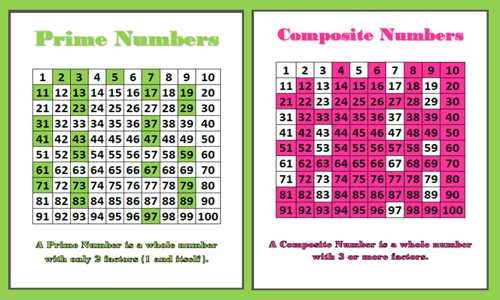
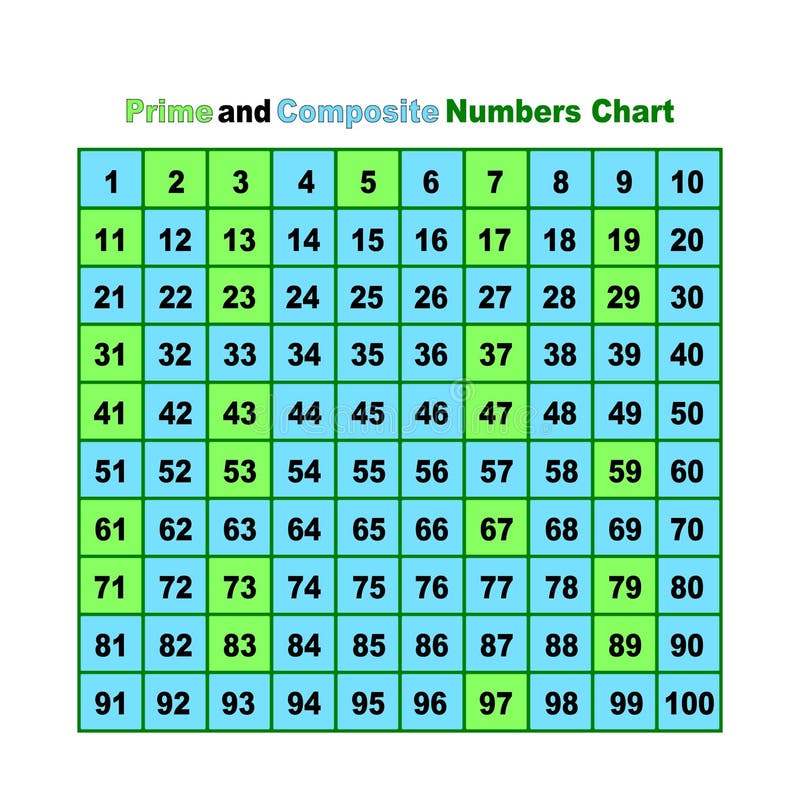
The Sieve of Eratosthenes is a classic method for identifying prime numbers. Developed by the ancient Greek mathematician Eratosthenes, this algorithm involves listing all numbers up to a certain limit. Subsequently, eliminating multiples of prime numbers one by one, the numbers that remain are prime.
For example, start with numbers up to 100. First, eliminate all multiples of 2 (except 2 itself), then multiples of 3 (except 3 itself), and so on. The numbers that remain, such as 2, 3, 5, 7, 11, and so forth, are all prime numbers.
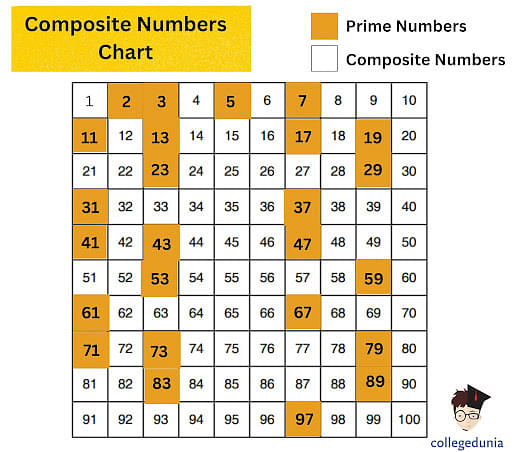
Composite Numbers: Made of Primes
In contrast to prime numbers, composite numbers are whole numbers that can be divided evenly by more than just 1 and themselves. They are, in essence, 'composed' of prime number factors.
For example, 4 is a composite number because it can be divided by 1, 2, and 4. Similarly, 6 can be divided by 1, 2, 3, and 6. This makes 4 and 6 composites.
Prime Factorization
A crucial concept related to composite numbers is prime factorization. Every composite number can be expressed as a unique product of prime numbers. For instance, 12 can be broken down into 2 x 2 x 3.
This unique prime factorization is a fundamental theorem of arithmetic, showing how primes are foundational in number theory. Understanding prime factorization simplifies calculations in various fields of math.
Is 53 a Prime or Composite Number?
Now, back to the original question: is 53 a prime or composite number? To determine this, we must check if 53 is divisible by any number other than 1 and itself.
Let's test it. 53 is not divisible by 2, 3, 5, or 7 (the prime numbers less than the square root of 53). Since we've checked all the relevant primes and none divide 53 evenly, we can conclude that 53 is indeed a prime number.
Therefore, 53 joins the ranks of other prime numbers, such as 2, 3, 5, 7, 11, and so on.
The Significance of Prime Numbers
Prime numbers are much more than just mathematical curiosities. They have crucial applications in various fields, most notably in cryptography, the science of secure communication.
Modern encryption methods, like RSA (Rivest-Shamir-Adleman), rely on the fact that it is easy to multiply two large prime numbers. However, factoring the result back into its original prime factors is computationally difficult.
This one-way function – easy to compute in one direction but difficult in the reverse – is the cornerstone of much of modern online security. Secure transactions, encrypted emails, and digital signatures depend on the properties of prime numbers.
Prime numbers are also used in hashing algorithms in computer science, particularly in creating hash tables. Choosing a prime number for the size of the hash table helps to minimize collisions, ensuring efficient data storage and retrieval.
"Without prime numbers, the internet as we know it would not exist." - A quote from a leading cryptographer about the role of primes in cybersecurity.
Beyond the Practical: The Beauty of Prime Numbers
Beyond their practical applications, prime numbers have fascinated mathematicians and thinkers for centuries. Their seemingly random distribution and the unresolved mysteries surrounding them continue to inspire research and exploration.
The Riemann Hypothesis, one of the most famous unsolved problems in mathematics, relates to the distribution of prime numbers. Proving or disproving this hypothesis could unlock deeper insights into the nature of primes and potentially lead to breakthroughs in various scientific fields.
Even without understanding the complex mathematics, one can appreciate the elegance and mystery of prime numbers. They are like stars in the night sky – seemingly scattered at random, yet governed by underlying principles waiting to be discovered.
Conclusion: A Simple Question, a Deeper Understanding
The initial question of whether 53 is prime or composite led us on a journey through number theory, from basic definitions to advanced applications. We've seen that identifying 53 as a prime number is only the beginning.
Understanding the nature of prime numbers and composite numbers opens up a world of mathematical concepts, practical applications, and philosophical contemplation. It also shows us that even seemingly simple questions can lead to profound insights.
As the group of friends around the table disperses, the chalkboard, now erased, carries an invisible reminder: the pursuit of knowledge, however simple it may seem, always leads to a deeper appreciation of the world around us.