Is 59 A Composite Or Prime Number

For many, the world of numbers holds a certain intrigue, a landscape of patterns and properties waiting to be discovered. Recently, the question of whether the number 59 is a composite or prime number has sparked curiosity among math enthusiasts and everyday individuals alike.

This seemingly simple query holds significance because it touches upon the fundamental building blocks of number theory. Understanding the nature of numbers like 59 helps us appreciate the structure of our mathematical universe and has implications for fields like cryptography and computer science. This article will delve into the properties of 59 to determine its classification.

Prime vs. Composite: The Defining Difference

Before we can definitively classify 59, it's crucial to understand the difference between prime and composite numbers. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.

In contrast, a composite number is a whole number greater than 1 that has more than two divisors. This means it can be divided evenly by numbers other than 1 and itself.

Determining the Divisibility of 59

To determine whether 59 is prime or composite, we need to check its divisibility. We can do this by attempting to divide 59 by whole numbers less than its square root (approximately 7.68). This is because if 59 has a divisor greater than its square root, it must also have a divisor smaller than its square root.

The numbers we need to check are 2, 3, 4, 5, 6, and 7. Let's examine each of these divisors. 59 is not divisible by 2 because it is an odd number.

59 is not divisible by 3. The sum of its digits (5 + 9 = 14) is not divisible by 3. 59 is not divisible by 4 because it is not divisible by 2 (or because its last two digits, 59, are not divisible by 4).

59 is not divisible by 5 because it does not end in 0 or 5. 59 is not divisible by 6 because it is not divisible by both 2 and 3. 59 is not divisible by 7. When dividing 59 by 7, we get a quotient of 8 with a remainder of 3.

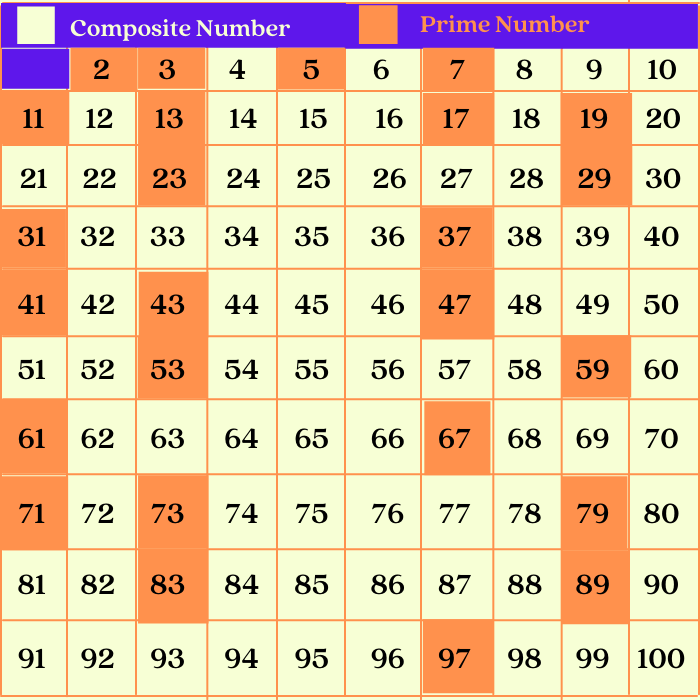
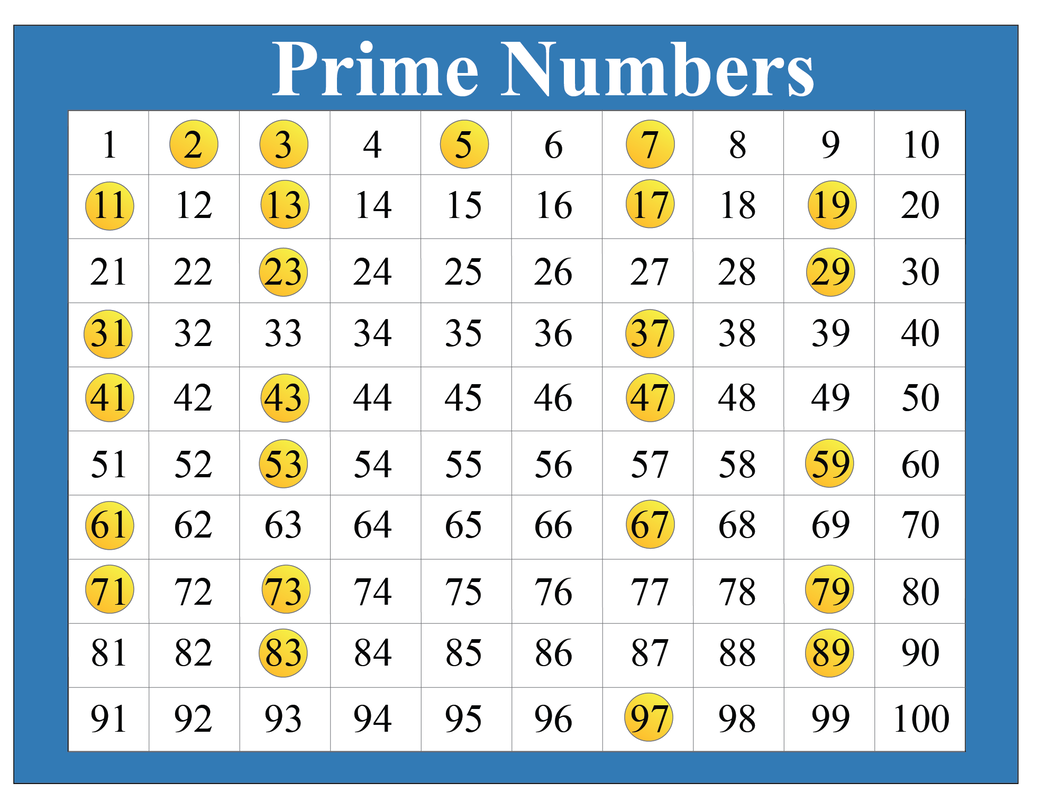
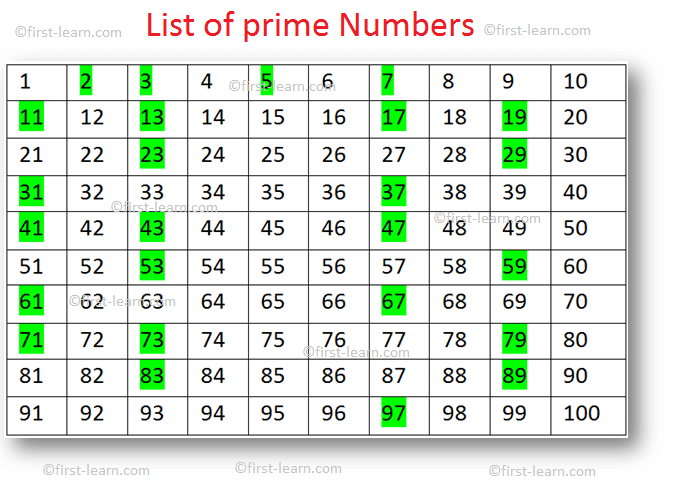
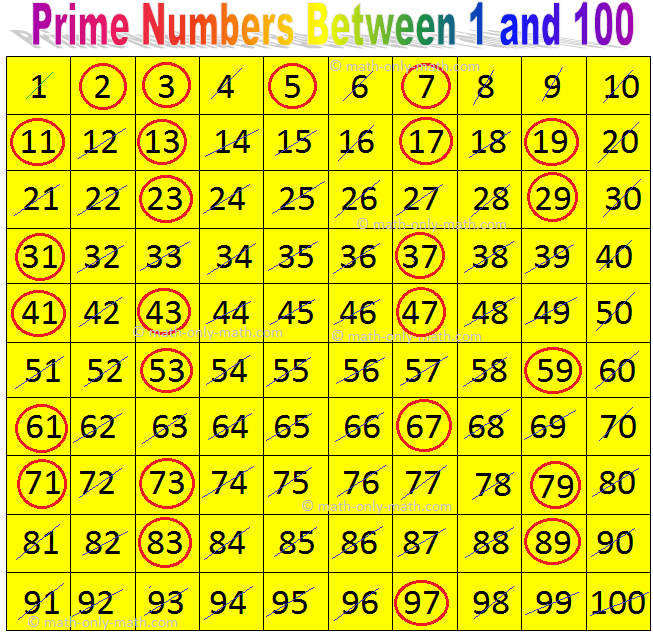
The Verdict: 59 is Prime

Having exhaustively checked for divisors up to its square root, we find that 59 is only divisible by 1 and itself. Therefore, 59 is definitively a prime number.

This determination aligns with established mathematical principles and can be verified using various online resources and mathematical tables. Resources like the Online Encyclopedia of Integer Sequences (OEIS) and the Prime Number Theorem support the claim that 59 is a prime number.

Significance and Application

While the classification of 59 as a prime number may seem trivial, understanding prime numbers is crucial in various fields. Prime numbers form the foundation of encryption algorithms used to secure online communication and financial transactions.

Algorithms like RSA rely on the difficulty of factoring large numbers into their prime components. Knowing that a number is prime also helps in generating random numbers, which are essential in simulations, statistical analysis, and many other areas of computer science.

For the average person, understanding prime numbers can spark an appreciation for the elegant structure underlying mathematics. It also reinforces the importance of critical thinking and logical reasoning in everyday life.

Conclusion

In conclusion, through careful examination of its divisibility, we can confidently state that 59 is indeed a prime number. This seemingly simple fact has profound implications for various fields and serves as a testament to the beauty and importance of mathematical principles.