Is 61 A Prime Number Or A Composite Number

Imagine a cozy classroom, sunlight streaming through the windows, illuminating the eager faces of young students. A chalkboard stands at the front, adorned with numbers and mathematical symbols. Today's question, written in bold chalk: "Is 61 a prime number or a composite number?"

The question of whether 61 is a prime or composite number is a foundational concept in mathematics, influencing our understanding of number theory and its many applications. While seemingly simple, this inquiry delves into the core characteristics of numbers and their divisibility. Determining the nature of 61 provides a clear example of prime number identification and the factors that define composite numbers.

What are Prime and Composite Numbers?

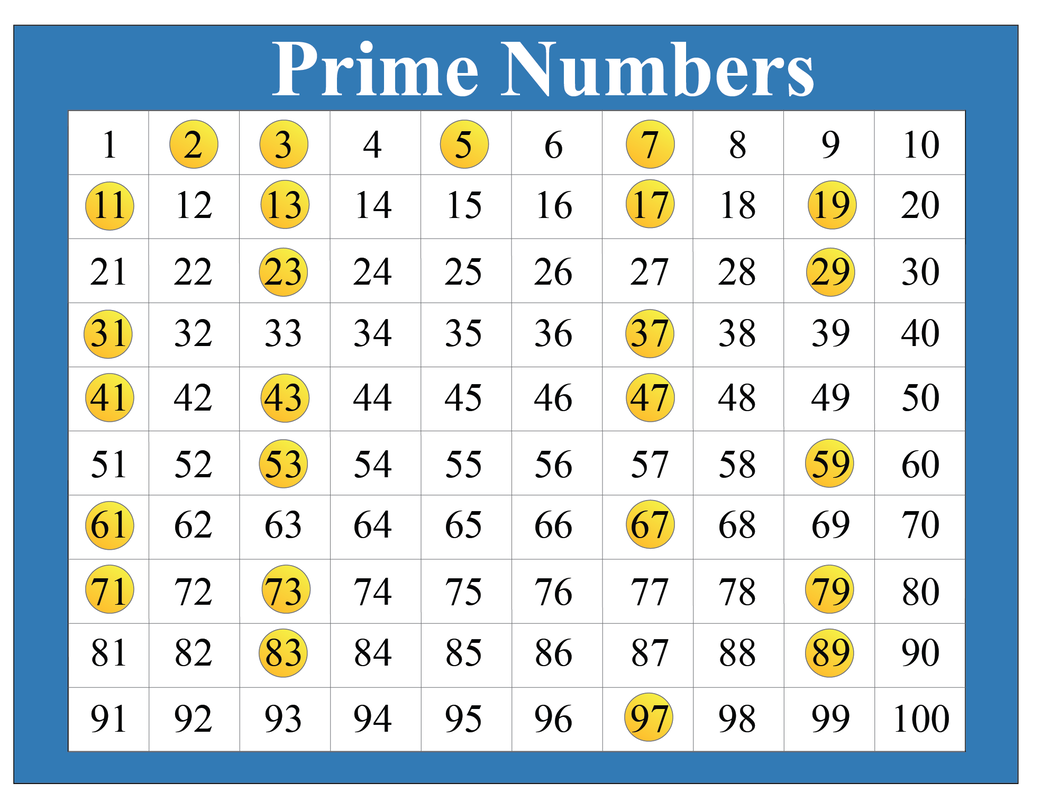
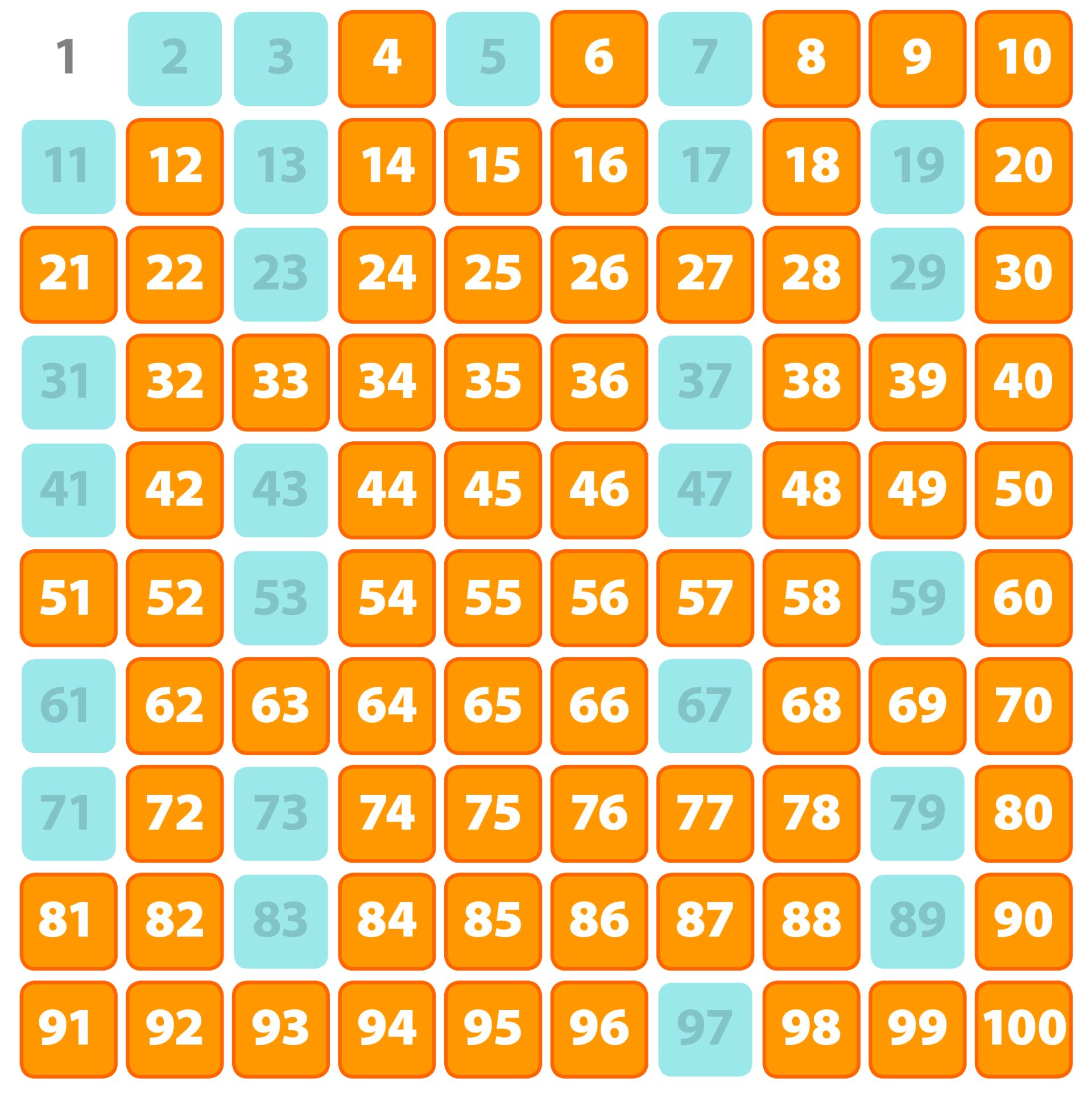
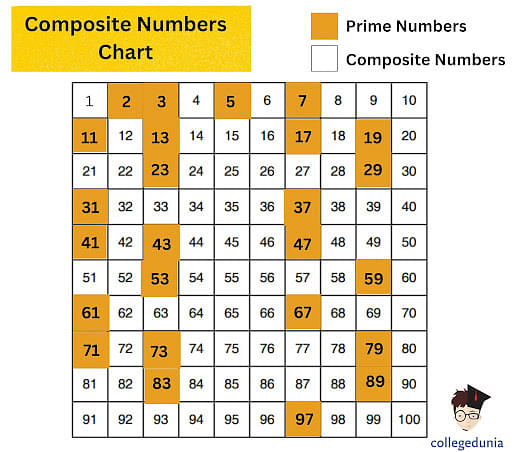
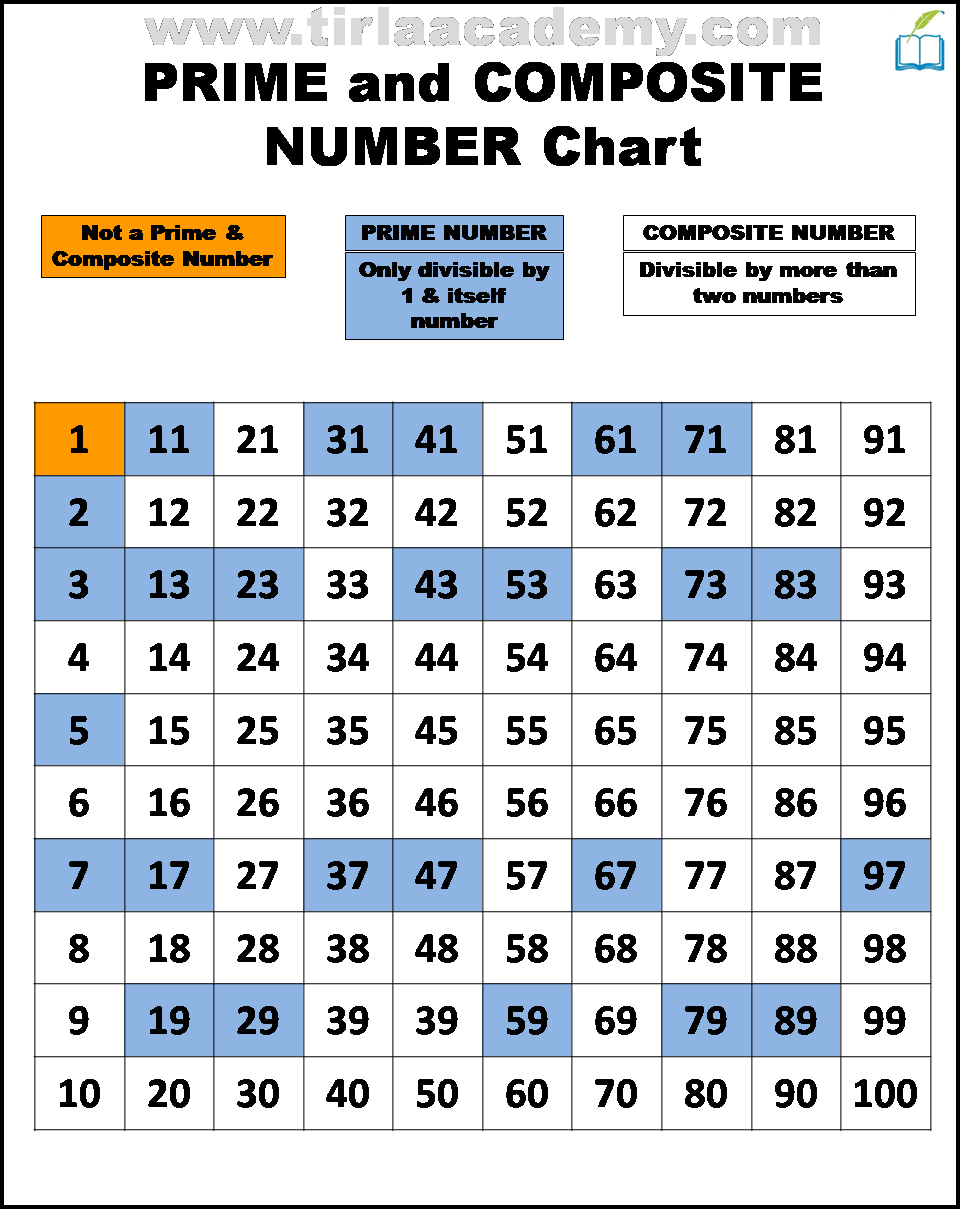
To answer our central question, we must first understand the definitions of prime and composite numbers. A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself. 2, 3, 5, and 7 are all prime numbers.

Conversely, a composite number is a whole number greater than 1 that has more than two distinct positive divisors. For instance, 4, 6, 8, and 9 are composite numbers.

The number 1 is neither prime nor composite. It's a special case with only one divisor, itself.

The Sieve of Eratosthenes

The concept of prime numbers is ancient, dating back to early mathematical explorations. The Sieve of Eratosthenes, developed by the Greek mathematician Eratosthenes of Cyrene, is a simple algorithm for finding all prime numbers up to a specified integer.

The sieve works by iteratively marking the multiples of each prime, starting with 2. The remaining unmarked numbers are prime.

This method, though ancient, provides a clear and accessible way to identify prime numbers and continues to be taught in classrooms today.

Determining if 61 is Prime or Composite

Now, let's determine whether 61 is prime or composite. We need to check if it's divisible by any number other than 1 and 61 itself.

We can start by testing divisibility by prime numbers less than the square root of 61 (which is approximately 7.8). This includes checking divisibility by 2, 3, 5, and 7.

61 is not divisible by 2, as it's an odd number. It's also not divisible by 3, as the sum of its digits (6 + 1 = 7) is not divisible by 3. Moreover, 61 does not end in 0 or 5, so it's not divisible by 5. Finally, 61 divided by 7 results in approximately 8.71, meaning it is not divisible by 7.

Since 61 is not divisible by any prime number less than its square root, we can confidently conclude that 61 is a prime number. Its only divisors are 1 and 61.

The Significance of Prime Numbers

Prime numbers are not just abstract mathematical concepts; they play a critical role in many real-world applications. Their unique properties make them essential for cryptography and data security.

Modern encryption methods, such as the RSA algorithm, rely heavily on the difficulty of factoring large numbers into their prime factors. The larger the prime numbers used, the more secure the encryption.

Furthermore, prime numbers are used in hashing algorithms, computer science, and even in the design of gear systems to ensure even wear.

"Without prime numbers, the digital world as we know it wouldn't exist," says Dr. Anya Sharma, a professor of mathematics at the University of California, Berkeley. "They are the bedrock of modern cybersecurity and countless other technologies."

Exploring Further: Prime Factorization

While 61 itself is a prime number, it's important to understand the concept of prime factorization. Prime factorization is the process of expressing a composite number as a product of its prime factors.

For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). Prime factorization is a fundamental concept in number theory and is used in many applications.

Understanding prime factorization helps us to analyze the properties of numbers and solve various mathematical problems.

The Beauty and Intrigue of Numbers

The question of whether 61 is prime or composite serves as an entry point into the fascinating world of number theory. Numbers, often taken for granted, hold deep mathematical truths and patterns.

Exploring these patterns, whether through identifying prime numbers or understanding composite numbers, allows us to appreciate the elegance and precision of mathematics.

It also reminds us that even seemingly simple questions can lead to profound insights and real-world applications.

A Concluding Reflection

So, returning to that sunlit classroom, we can now confidently answer the question: 61 is indeed a prime number. This simple determination opens a door to understanding the fundamental building blocks of numbers and their significance in our daily lives.

From securing our online transactions to designing efficient computer algorithms, prime numbers are silently at work, shaping the world around us. The exploration of mathematics, even in its simplest forms, can inspire curiosity and unlock the beauty of abstract thought.

And who knows? Perhaps one of those students in that sunlit classroom will one day make a groundbreaking discovery in the realm of number theory, inspired by the simple question: "Is 61 a prime number or a composite number?"