Is 75 A Prime Number Or A Composite Number

Imagine a warm classroom filled with the buzz of young minds grappling with numbers. Sunlight streams through the window, illuminating colorful charts of multiplication tables and prime number lists. A student, brow furrowed in concentration, stares intently at the number 75, a question hanging in the air: Is it a building block or something more complex?
At its heart, the question of whether 75 is a prime or composite number is more than just a mathematical puzzle. Understanding its nature unlocks a deeper understanding of number theory, prime factorization, and the elegant structure underlying our entire numerical system. This article explores the fascinating world of prime and composite numbers, using 75 as our guide, to reveal why this distinction is important and how it impacts various aspects of mathematics and beyond.
Delving into Prime and Composite Numbers
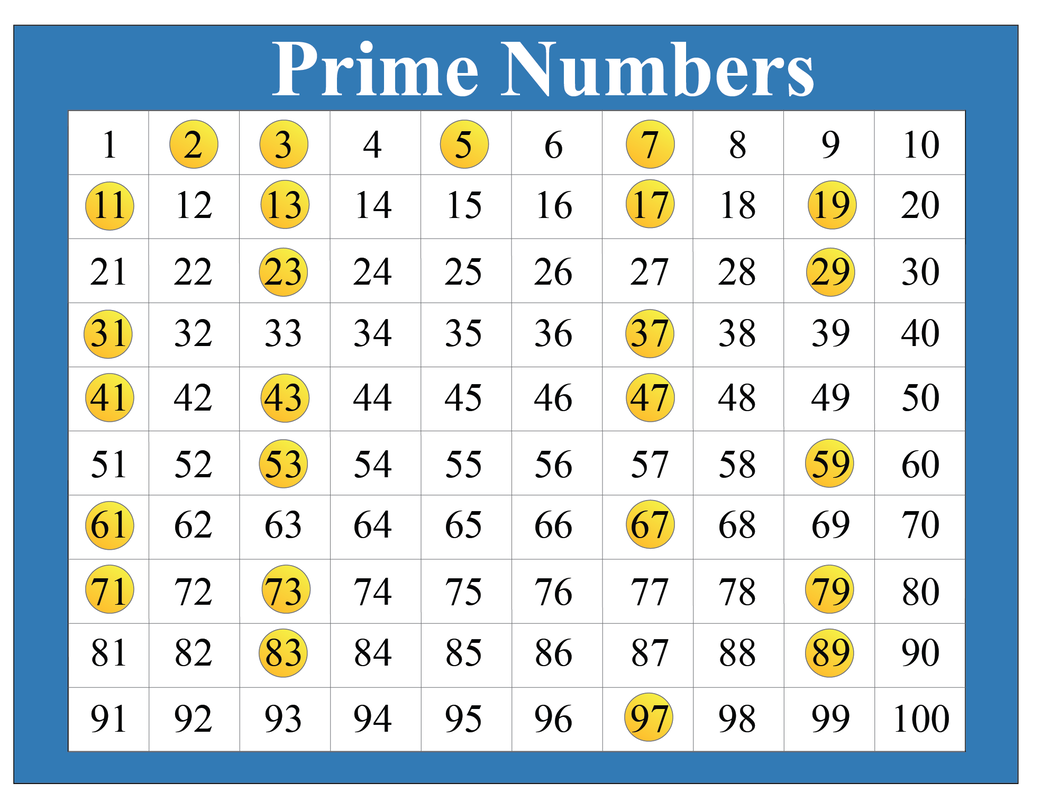
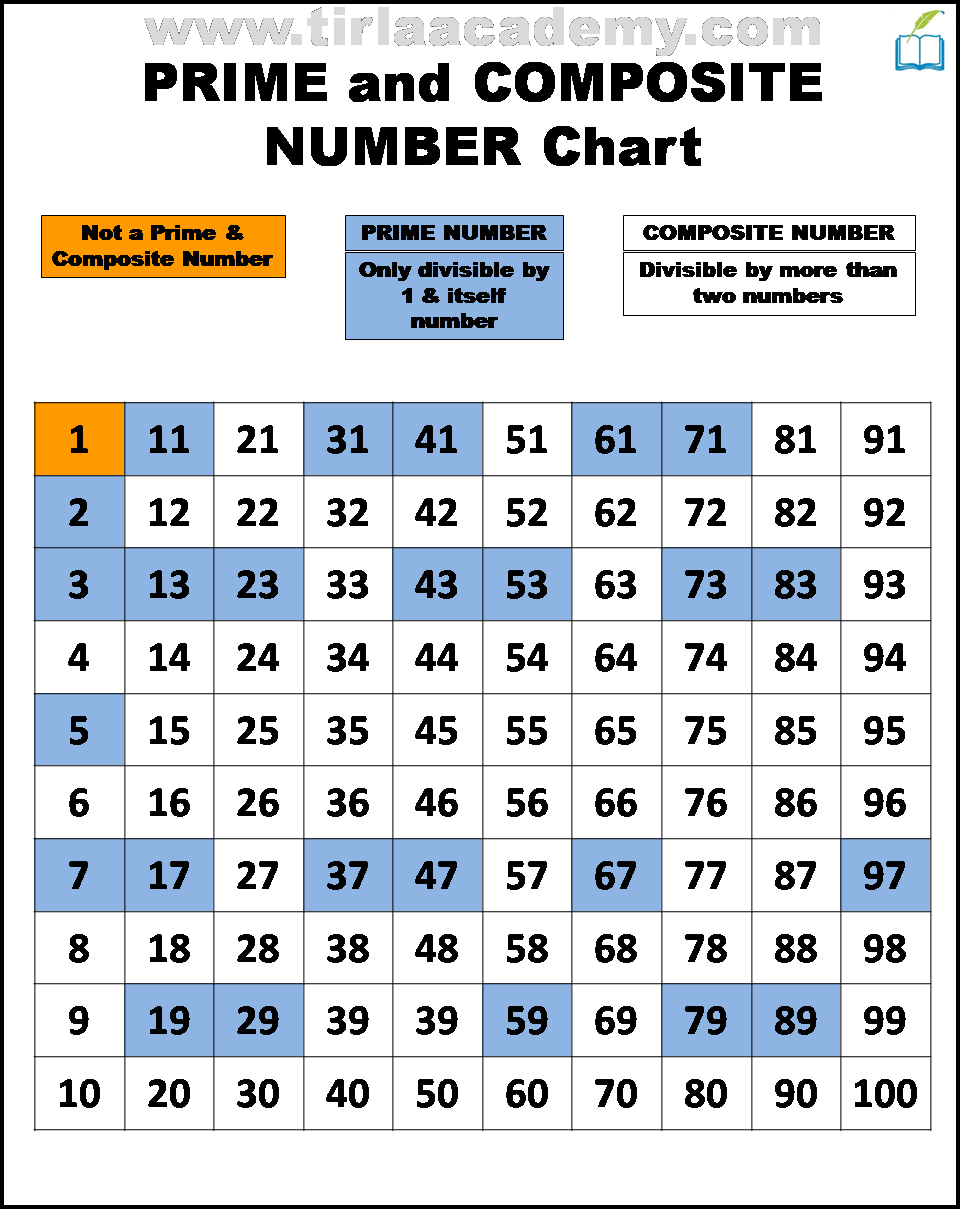
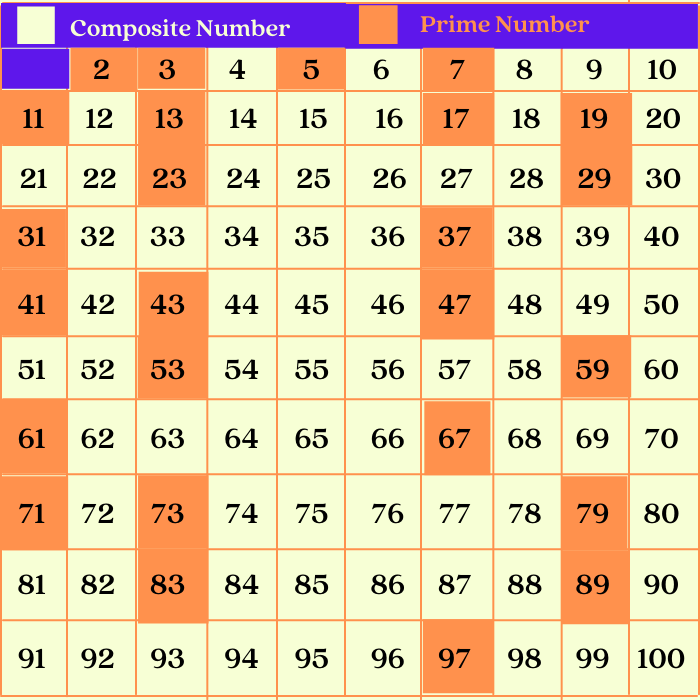
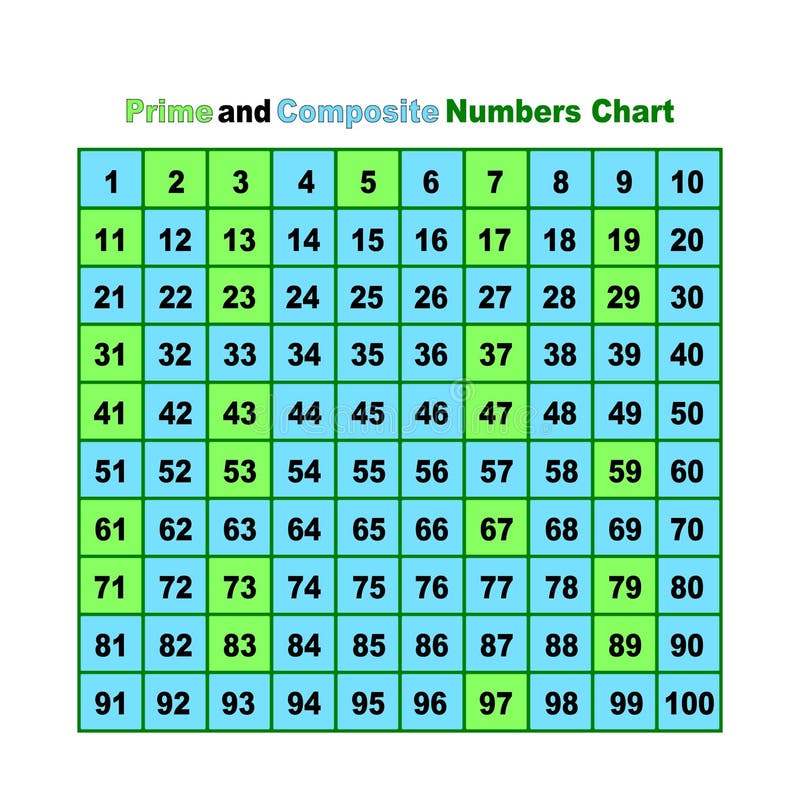
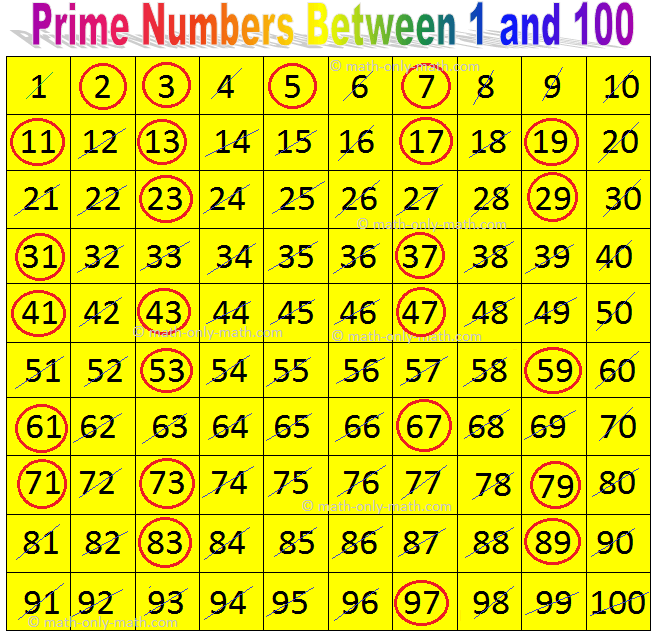
Let's start with the basics. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Think of 2, 3, 5, 7, 11 – each one is only divisible by 1 and the number itself.
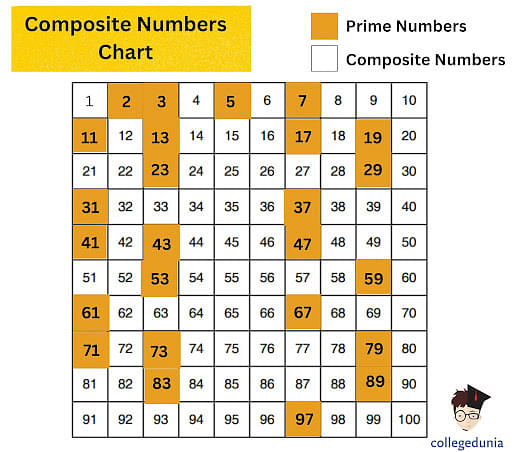
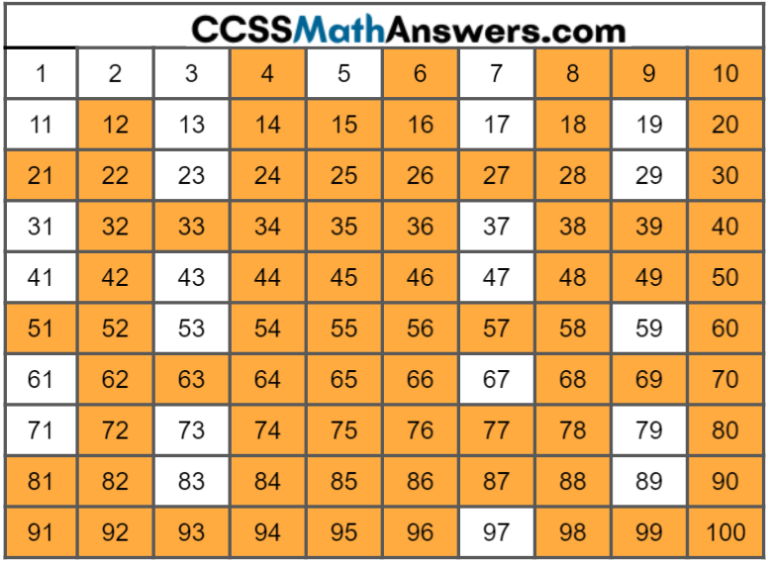
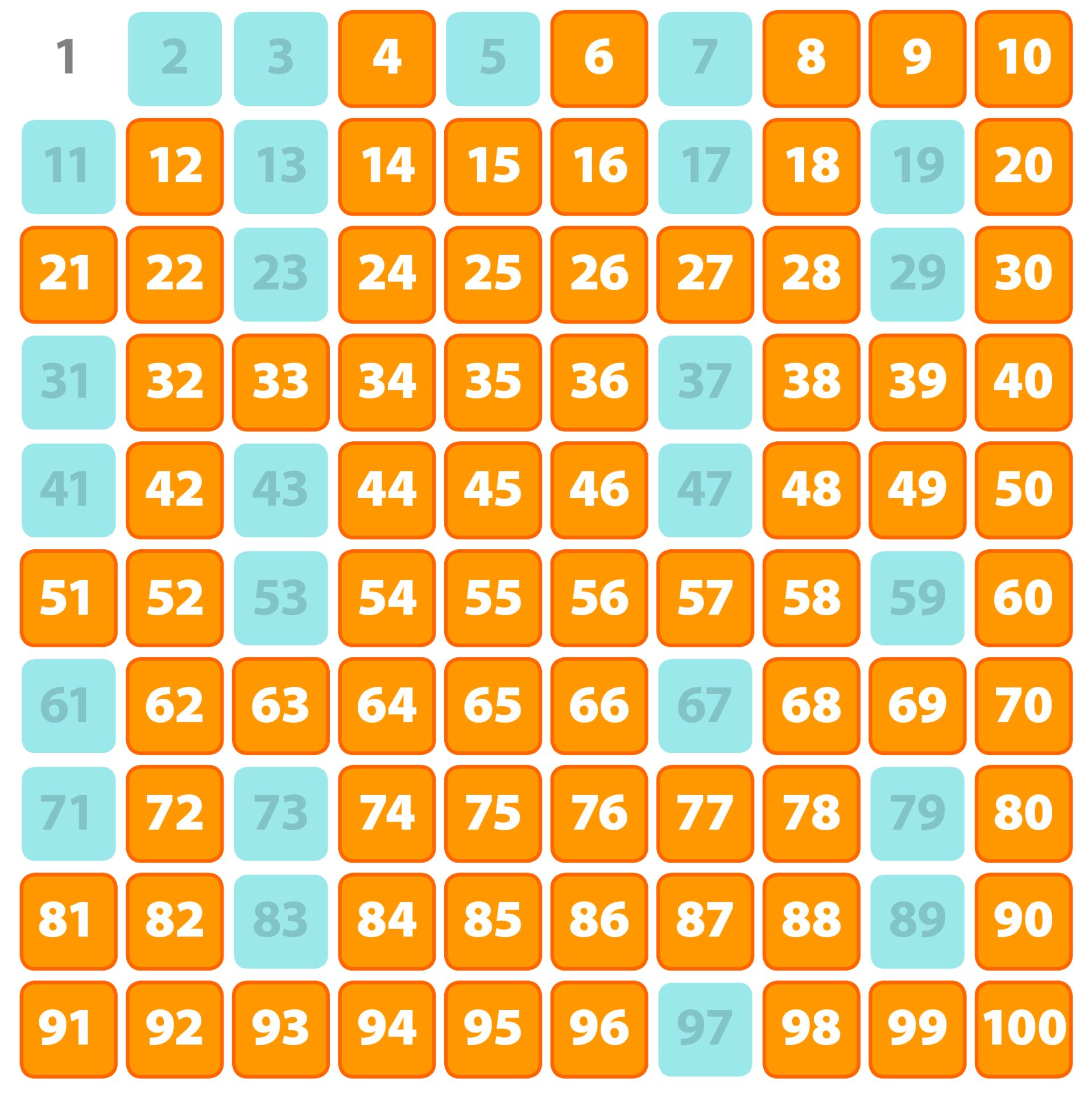
On the other hand, a composite number is a whole number greater than 1 that has more than two divisors. That means it can be divided evenly by 1, itself, and at least one other number.
Identifying the Nature of 75
Now, back to our number, 75. To determine if it's prime or composite, we need to find its divisors. We know it's divisible by 1 and 75.
But can we divide it evenly by anything else? A quick check reveals that 75 is divisible by 3 (75 / 3 = 25) and 5 (75 / 5 = 15). Therefore, it has more than two divisors.
Since 75 is divisible by 1, 3, 5, 15, 25, and 75, we can confidently conclude that 75 is a composite number. It’s not a fundamental building block like a prime; it's constructed from other numbers.
The Significance of Prime and Composite Numbers
The distinction between prime and composite numbers isn't just a theoretical exercise. It has real-world applications in various fields. Prime numbers, in particular, play a crucial role in cryptography and computer security.
Many encryption algorithms rely on the difficulty of factoring large numbers into their prime components. The larger the prime numbers used, the more secure the encryption becomes.
Composite numbers, while not directly used in encryption, are essential for understanding how numbers are built and related to each other. They demonstrate the concept of factorization, which is vital in simplifying fractions, solving equations, and understanding number patterns.
Prime Factorization: Unveiling the Building Blocks of 75
One of the most useful concepts related to prime and composite numbers is prime factorization. This is the process of breaking down a composite number into its prime factors, the prime numbers that multiply together to give the original number.
To find the prime factorization of 75, we can start by dividing it by the smallest prime number that divides it evenly, which is 3. This gives us 75 = 3 * 25.
Now, we need to factor 25. It's divisible by 5, another prime number, giving us 25 = 5 * 5. Therefore, the prime factorization of 75 is 3 * 5 * 5, or 3 * 52.
Real-World Applications and Beyond
Understanding prime and composite numbers extends beyond theoretical mathematics. The concepts have practical applications in coding, computer science, and even in understanding natural phenomena. For example, certain patterns in nature, like the distribution of cicada life cycles, are thought to be influenced by prime numbers to minimize the risk of predators synchronizing their life cycles.
Moreover, the pursuit of larger and larger prime numbers continues to fascinate mathematicians. The Electronic Frontier Foundation offers prizes for discovering new primes of specific sizes, further emphasizing the relevance and intrigue surrounding these fundamental numbers.
The seemingly simple question of whether 75 is prime or composite leads us into a deeper appreciation for the beauty and complexity of mathematics. It reminds us that even seemingly basic concepts can have profound implications.
Conclusion: The Beauty of Number Theory
The journey through the world of prime and composite numbers, using 75 as our example, reveals a fascinating intersection of theoretical mathematics and practical application. While 75 is clearly a composite number, its analysis sheds light on the fundamental building blocks of our numerical system.
By understanding the concepts of prime and composite numbers, we gain a valuable tool for problem-solving, critical thinking, and appreciating the elegant structure that underlies the world around us. From securing our digital communications to deciphering patterns in nature, the impact of these seemingly simple numbers is profound and far-reaching.
So, the next time you encounter a number, take a moment to consider its nature – is it a prime, a fundamental building block, or a composite, built from other numbers? The answer might surprise you and unlock a new appreciation for the beauty of number theory. Just like that curious student in the sunlit classroom, we can all find wonder in the world of numbers.