The Curved Surface Area Of A Cylinder Is 4400

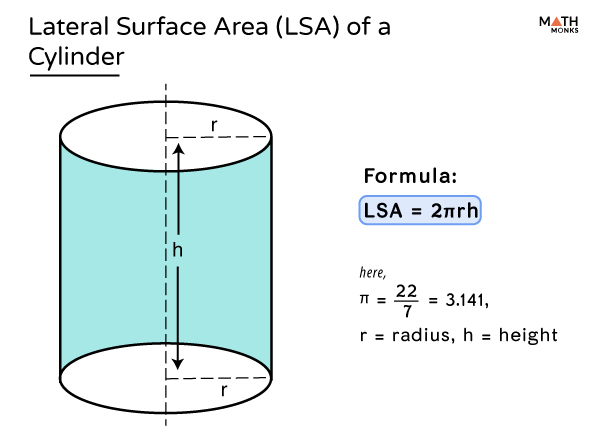
A seemingly simple mathematical problem, the determination of the radius and height of a cylinder given its curved surface area, has sparked renewed interest in mathematical education and its practical applications across various sectors. The problem, stating that the curved surface area of a cylinder is 4400 square units (without specifying the unit of measurement), has served as a valuable exercise in understanding geometric principles.

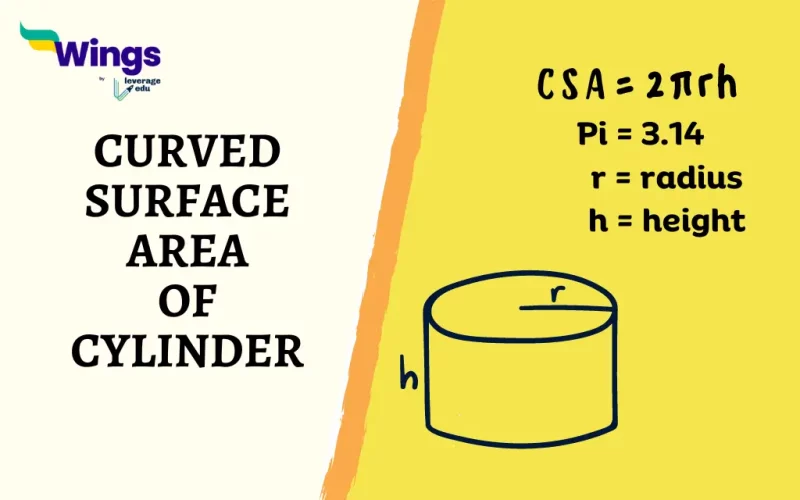
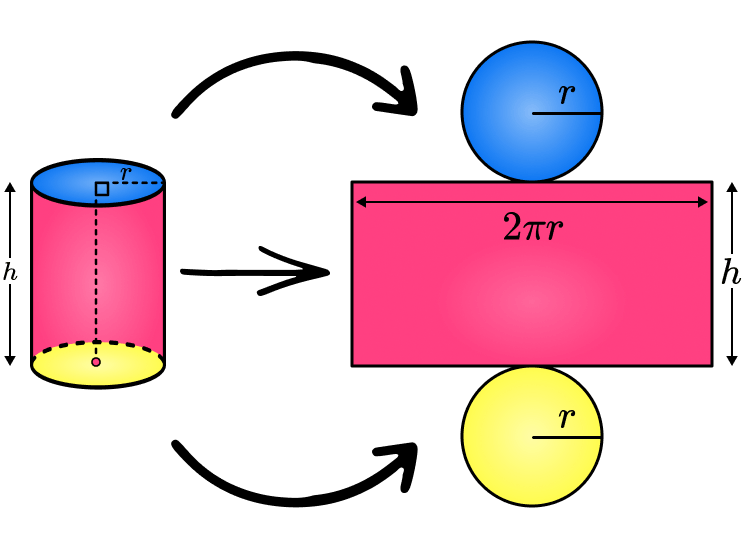
This calculation, while appearing purely theoretical, underscores the importance of mathematical literacy in fields ranging from engineering and architecture to manufacturing and even data analysis. The exercise necessitates utilizing the formula for the curved surface area of a cylinder, which is 2πrh, where 'r' represents the radius and 'h' the height.

Significance of the Problem

While the problem itself might seem abstract, its significance lies in reinforcing critical mathematical concepts. Understanding and applying formulas, manipulating variables, and solving equations are all essential skills honed through such exercises. These skills are fundamental for problem-solving in numerous real-world scenarios.

Key Details and Implications

The challenge stems from the single equation (2πrh = 4400) having two unknowns, 'r' and 'h'. This means that there are infinitely many possible solutions, illustrating the concept of indeterminacy in mathematics. Students are encouraged to explore different possible radii and heights that satisfy the equation.

Educators are leveraging this problem to illustrate the relationship between different variables and the concept of constraint. Real-world applications often involve multiple constraints, making this type of exercise valuable in preparing students for complex engineering and design challenges.

Impact on Education and Beyond

The resurgence of interest in this particular problem has been fueled by its inclusion in various educational resources and online learning platforms. Many teachers are using this as an opportunity to show the real world relation of maths.

This helps to reinforce mathematical learning among students. Increased attention on the equation can lead to a greater number of students getting the right answers.

Beyond the classroom, the principles demonstrated by this problem apply to various industries. For example, engineers designing cylindrical tanks or pipelines need to carefully consider the relationship between radius, height, and surface area. An important consideration is also the material used.

A Human Interest Angle

Consider *Sarah Chen*, a high school student who initially struggled with geometry. Through solving variations of this cylinder problem, she gained a deeper understanding of mathematical concepts. Sarah then used her new skills to design a more efficient irrigation system for her family’s farm, demonstrating the practical impact of mathematical literacy.

Expert Opinions

“This problem highlights the importance of applied mathematics in everyday life,” says Dr. Emily Carter, a professor of mathematics education at a leading university. “It demonstrates that mathematical concepts are not just abstract theories, but valuable tools for solving real-world problems.”

“The cylinder problem is a valuable teaching tool that helps students bridge the gap between theory and practice,” says *Mr. David Lee*, a high school math teacher. This kind of equation is important to solve.