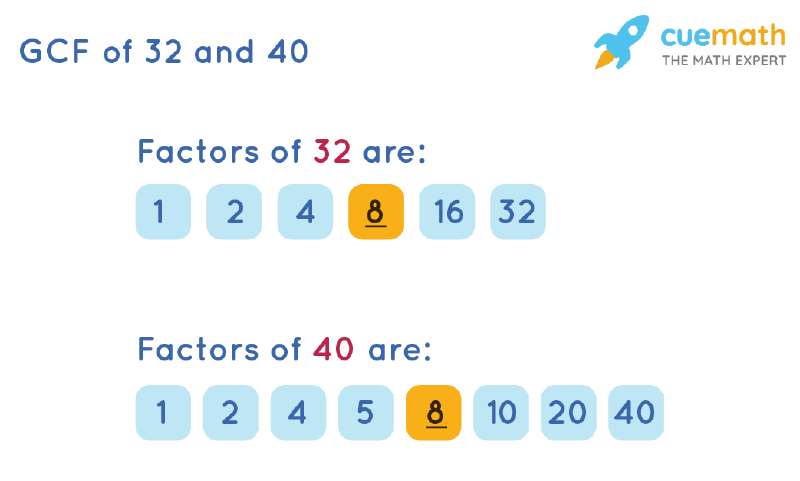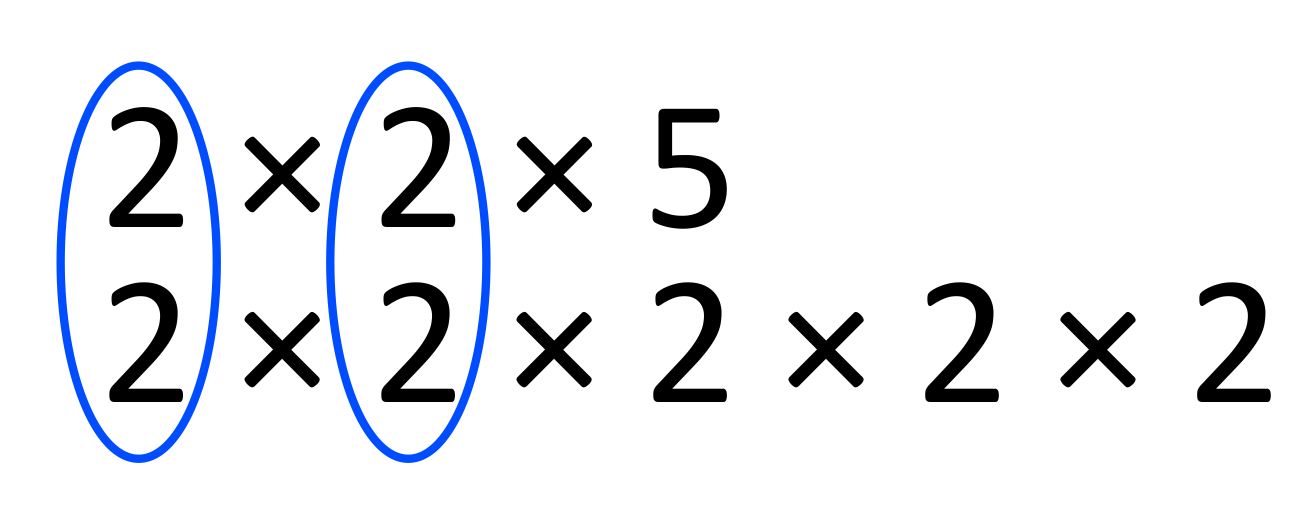What Is The Greatest Common Factor Of 40 And 32

Breaking: Confusion reigns as individuals struggle to identify the Greatest Common Factor (GCF) of 40 and 32. Misunderstandings could impact basic mathematical operations.
The Greatest Common Factor, a fundamental concept in mathematics, determines the largest number that divides evenly into two or more numbers. Incorrectly identifying it can lead to errors in simplification, fractions, and other calculations.
The Answer: 8
The GCF of 40 and 32 is 8. This means that 8 is the largest number that divides both 40 and 32 without leaving a remainder.
Here's how to determine the GCF:
Listing Factors
One method is to list all the factors of each number. The factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40. The factors of 32 are 1, 2, 4, 8, 16, and 32.
By comparing the lists, we can identify the largest factor common to both numbers, which is 8.
Prime Factorization
Another method involves prime factorization. Breaking down 40 into its prime factors gives us 2 x 2 x 2 x 5 (23 x 5). Similarly, breaking down 32 yields 2 x 2 x 2 x 2 x 2 (25).
To find the GCF, identify the common prime factors and their lowest powers. In this case, the common prime factor is 2, and the lowest power is 23, which equals 8.
Why This Matters
Understanding the GCF is crucial in various mathematical applications. It is essential in simplifying fractions to their lowest terms.
The GCF is also critical in solving problems related to ratios and proportions. Incorrect calculation can lead to inaccurate problem-solving.
Common Mistakes
One common mistake is confusing the GCF with the Least Common Multiple (LCM). The LCM is the smallest number that is a multiple of both numbers.
Another error is incorrectly listing the factors or prime factors of the numbers. Accuracy is paramount when applying these methods.
Expert Insight
"The Greatest Common Factor is a foundational concept," explains Dr. Anya Sharma, Professor of Mathematics at the Institute for Numerical Analysis. "Mastering it is crucial for success in more advanced mathematical topics."
Dr. Sharma stresses the importance of practice and repetition. She encourages students to use both listing factors and prime factorization methods.
Real-World Applications
The GCF is not limited to textbooks; it has real-world applications. Consider dividing 40 apples and 32 oranges into identical bags.
The GCF (8) tells us that we can create 8 bags, each containing 5 apples and 4 oranges. This concept is useful in resource allocation and problem solving.
Moving Forward
Educational resources are readily available for those struggling with the GCF. Online tutorials and practice worksheets offer valuable support.
Focus on mastering fundamental mathematical skills for future success. Seek help when needed and prioritize conceptual understanding.