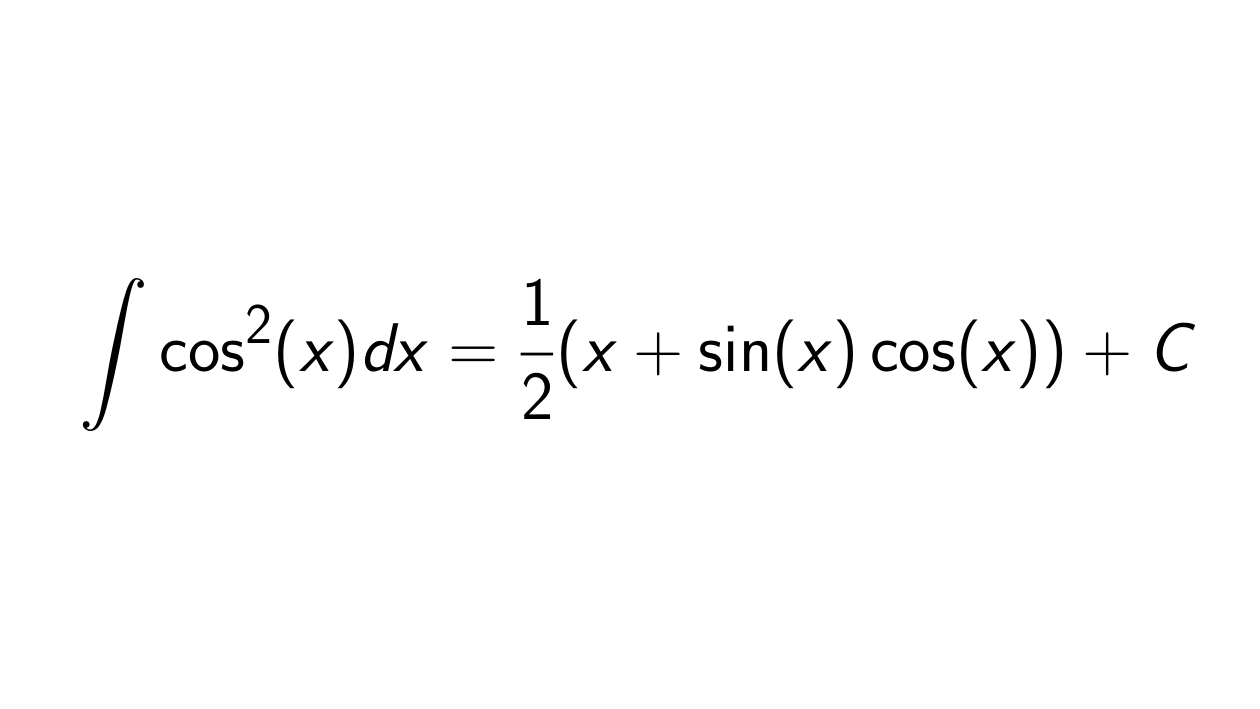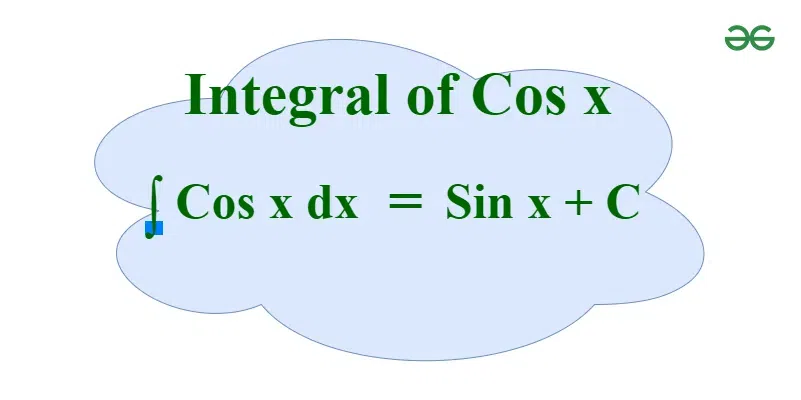What Is The Integral Of Cos

Imagine yourself on a serene beach, the rhythmic crash of waves providing a steady, calming beat. The sun, a radiant orb, warms your skin, and the gentle breeze whispers secrets of the sea. In the distance, you see patterns forming in the sand, intricate curves and slopes mirroring the rise and fall of the tide. Just as the ocean's ebb and flow can be described mathematically, so too can many natural phenomena. And at the heart of this mathematical description lies a fundamental question: What is the integral of cosine?

This seemingly simple question opens a door to a world of calculus, physics, and engineering. Knowing the integral of cosine is crucial for understanding everything from alternating current in electrical circuits to the behavior of sound waves. It is a building block upon which countless complex calculations are built.

The Basics: Understanding Integration

Before diving into the specifics of cosine, let's establish a foundation. Integration, at its core, is the reverse process of differentiation.

While differentiation helps us find the rate of change of a function, integration helps us find the area under the curve of a function. Think of it as summing up infinitesimally small slices to find the total.

Differentiation: The Opposite Side of the Coin

To truly grasp integration, we need to appreciate its relationship with differentiation. Remember that the derivative of sine (sin(x)) is cosine (cos(x)).

This is a critical piece of information because it directly informs the integral of cosine.

The Integral of Cosine: Unveiled

Now, let's tackle the main question: what is the integral of cos(x)? The answer, in its simplest form, is sin(x) + C.

Here, 'C' represents the constant of integration. This constant is vital because the derivative of any constant is zero, meaning we lose information about a constant term when differentiating.

Therefore, when integrating, we must acknowledge the possibility of an unknown constant.

The Significance of Cosine and its Integral

Cosine, along with sine, is one of the fundamental trigonometric functions. These functions are periodic, meaning they repeat their values at regular intervals.

This periodic nature makes them invaluable for modeling oscillating phenomena in the real world.

Applications in Physics

In physics, cosine and sine are ubiquitous. Consider the motion of a pendulum or a mass attached to a spring.

These systems exhibit simple harmonic motion, which can be accurately described using sinusoidal functions.

The integral of cosine then becomes essential for calculating displacement, velocity, and acceleration within these systems.

Electrical Engineering: Alternating Current

Alternating current (AC), the electricity that powers our homes, is another area where cosine reigns supreme. AC voltage and current vary sinusoidally with time.

Understanding the integral of cosine is crucial for analyzing AC circuits, calculating power consumption, and designing electrical systems.

Signal Processing: Decoding Information

Signal processing, the art of extracting information from signals, relies heavily on Fourier analysis. Fourier analysis decomposes complex signals into a sum of simpler sine and cosine waves.

This decomposition allows engineers to filter noise, compress data, and perform countless other tasks. The integral of cosine plays a vital role in the mathematical machinery of Fourier transforms.

Beyond the Basics: Definite Integrals

While the indefinite integral of cos(x) is sin(x) + C, we often encounter definite integrals in practice. A definite integral has upper and lower limits of integration.

For example, we might want to find the area under the cosine curve between x = 0 and x = π/2.

To do this, we evaluate sin(x) at the upper and lower limits and subtract the results: sin(π/2) - sin(0) = 1 - 0 = 1.

Common Mistakes and How to Avoid Them

When working with integrals, it's easy to make mistakes. One common error is forgetting the constant of integration 'C'.

Always remember to include it in indefinite integrals. Another pitfall is misapplying the rules of integration.

Double-check your formulas and be mindful of the chain rule when integrating composite functions. Practice and careful attention to detail are key to avoiding these mistakes.

The Enduring Relevance of Calculus

The integral of cosine, though seemingly simple, exemplifies the power and beauty of calculus. It is a fundamental tool that enables us to understand and model the world around us.

From the gentle sway of a pendulum to the complex workings of an electrical grid, the principles of calculus are at play.

By mastering these principles, we unlock a deeper understanding of the universe and gain the ability to solve problems that would otherwise be insurmountable.

As we reflect on the integral of cosine, we are reminded of the interconnectedness of mathematics and the physical world. This humble integral, a cornerstone of calculus, empowers us to unravel the mysteries of nature and build a better future. Embrace the challenge, explore the possibilities, and let the integral of cosine guide your journey.