What Is The Lcm For 16 And 24
In an era defined by data and precision, even seemingly simple mathematical concepts like the Least Common Multiple (LCM) hold profound significance. From optimizing manufacturing processes to scheduling complex logistical operations, the LCM plays an often-unseen but critical role in ensuring efficiency and minimizing waste. Understanding how to calculate the LCM for specific numbers, such as 16 and 24, is therefore not merely an academic exercise, but a practical necessity for professionals across various fields.
This article delves into the specifics of determining the LCM of 16 and 24, exploring various methodologies and highlighting its practical applications. We will examine prime factorization, listing multiples, and other common techniques, providing a comprehensive understanding of this fundamental mathematical concept. Our aim is to provide a clear and accessible guide, suitable for both those seeking a refresher and those encountering the LCM for the first time.
Understanding the Least Common Multiple
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of those numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. The concept is foundational in arithmetic and has wide-ranging applications in mathematics and beyond.
Consider the numbers 16 and 24. Finding their LCM involves identifying the smallest number that is a multiple of both. Various methods exist to achieve this, each offering its own advantages and disadvantages in terms of computational efficiency and ease of understanding.
Methods for Calculating the LCM of 16 and 24
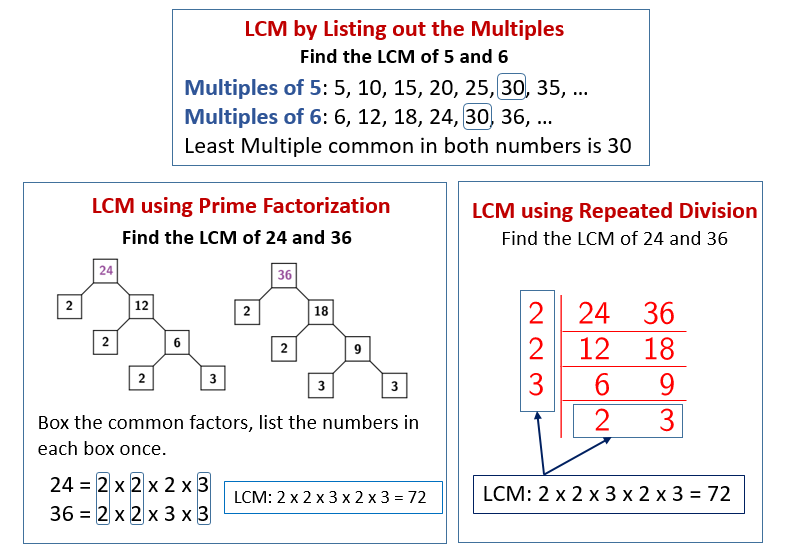
Listing Multiples
One of the most straightforward methods for finding the LCM is to list out the multiples of each number until a common multiple is found. This approach is particularly effective for smaller numbers like 16 and 24. However, it can become cumbersome for larger numbers where the common multiple appears much further down the list.
Multiples of 16: 16, 32, 48, 64, 80, 96... Multiples of 24: 24, 48, 72, 96, 120...
By examining these lists, we can see that 48 is the smallest number that appears in both. Therefore, the LCM of 16 and 24 is 48.
Prime Factorization
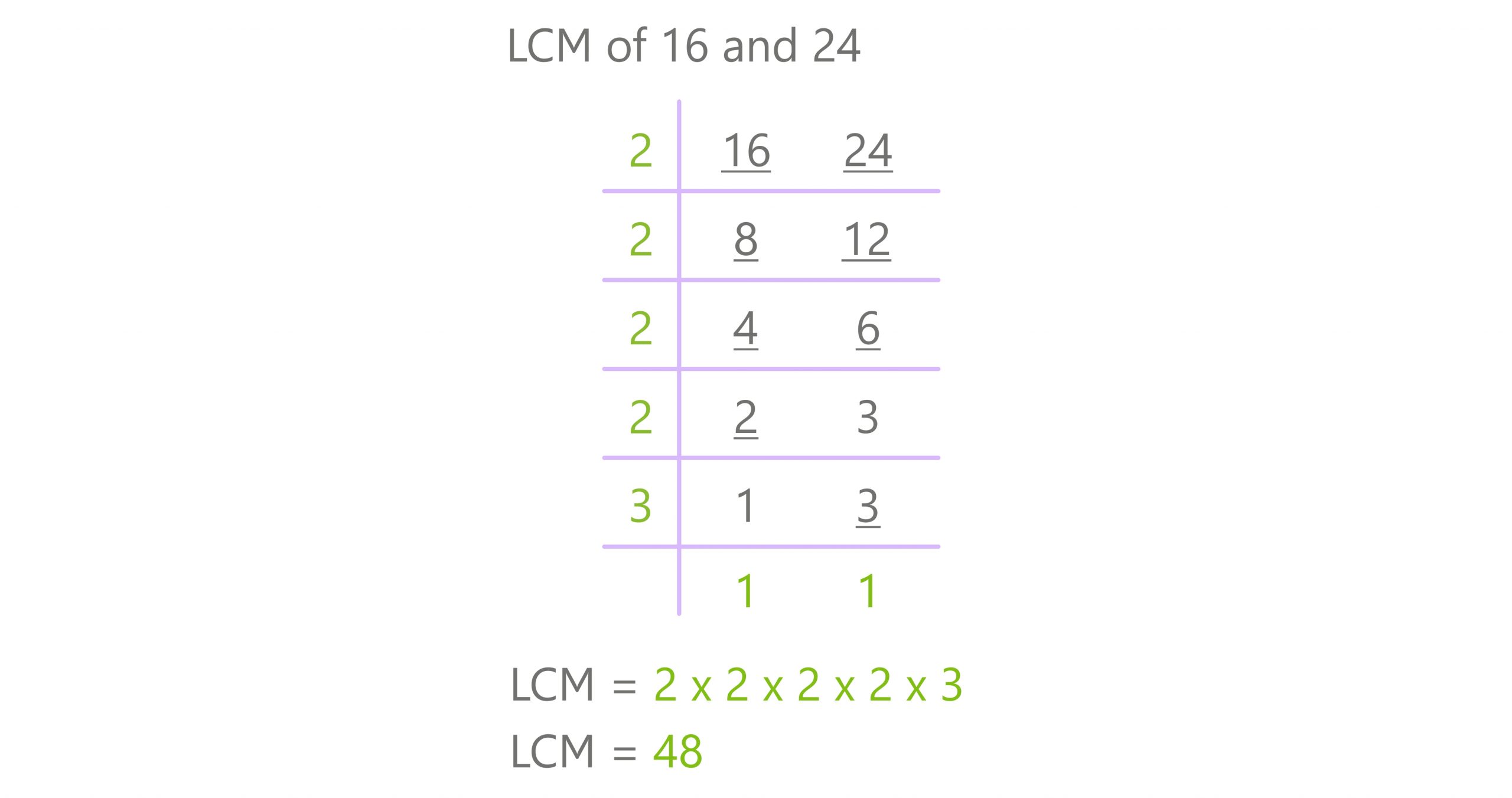
A more systematic approach involves prime factorization, breaking down each number into its prime factors. This method is especially useful for larger numbers where listing multiples becomes impractical. It provides a clear and structured way to identify the common and unique prime factors required to construct the LCM.
The prime factorization of 16 is 2 x 2 x 2 x 2, or 24. The prime factorization of 24 is 2 x 2 x 2 x 3, or 23 x 3.
To find the LCM, we take the highest power of each prime factor present in either factorization. In this case, the highest power of 2 is 24 (from 16) and the highest power of 3 is 31 (from 24). Thus, the LCM is 24 x 3 = 16 x 3 = 48.
Using the Greatest Common Divisor (GCD)
The LCM can also be calculated using the Greatest Common Divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship between LCM and GCD is expressed by the formula: LCM(a, b) = (a x b) / GCD(a, b).
First, find the GCD of 16 and 24. The factors of 16 are 1, 2, 4, 8, and 16. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. The greatest common factor is 8.
Then, calculate the LCM using the formula: LCM(16, 24) = (16 x 24) / 8 = 384 / 8 = 48. Therefore, the LCM is 48.
Practical Applications of the LCM
While the calculation of the LCM may seem abstract, it has numerous real-world applications. From optimizing workflows to resolving scheduling conflicts, the LCM plays a crucial role in various industries and daily tasks. Understanding the LCM is essential for anyone seeking to improve efficiency and make informed decisions.
In manufacturing, the LCM is used to determine the optimal batch sizes to minimize waste and ensure smooth production runs. For example, if one machine completes a task every 16 seconds and another completes a task every 24 seconds, the LCM (48 seconds) would indicate the time interval at which both machines will complete their tasks simultaneously, allowing for efficient coordination.
In scheduling, the LCM is essential for coordinating events that occur at regular intervals. If one event happens every 16 days and another event happens every 24 days, the LCM (48 days) indicates the time it will take for both events to occur on the same day again. This is useful for scheduling meetings, appointments, or other recurring events.
Conclusion
The LCM of 16 and 24 is 48, a result obtainable through various methods including listing multiples, prime factorization, and using the GCD. Understanding these different approaches provides a deeper comprehension of the concept and allows for its application in diverse situations.
Mastering the calculation and application of the LCM is a valuable skill, contributing to increased efficiency and improved decision-making in various domains. From optimizing production schedules to streamlining logistical operations, the LCM's relevance extends far beyond the classroom, solidifying its place as a fundamental concept in mathematics and its practical applications.
As technology continues to advance and data becomes increasingly central to our lives, the importance of mathematical literacy, including concepts like the LCM, will only continue to grow. Embracing these fundamentals is crucial for navigating the complexities of the modern world and making informed decisions based on sound mathematical principles.













/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)
