What Is The Lcm Of 10 And 25

In an era dominated by complex algorithms and intricate calculations, a seemingly basic mathematical concept continues to underpin countless technological and scientific advancements. The Least Common Multiple, or LCM, frequently emerges as a fundamental tool, quietly but crucially impacting everything from scheduling software to understanding planetary movements.
At its core, the question "What is the LCM of 10 and 25?" represents more than a simple arithmetic problem. This article delves into the practical applications and theoretical significance of the LCM, exploring its relevance across diverse fields and demonstrating its enduring importance in mathematical literacy.
Understanding the LCM: A Definition
The Least Common Multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of those numbers. Finding the LCM of 10 and 25 involves identifying the smallest number that both 10 and 25 divide into without leaving a remainder. The result is 50.
This seemingly simple calculation possesses considerable power in simplifying and solving more complex mathematical problems.
Methods for Determining the LCM
Several established methods exist for determining the LCM of two or more numbers. Each approach offers a slightly different perspective on the concept and caters to different levels of mathematical proficiency.
Listing Multiples
One basic method involves listing out the multiples of each number until a common multiple is found. Multiples of 10: 10, 20, 30, 40, 50, 60… Multiples of 25: 25, 50, 75… The first common multiple identified, 50, is the LCM.
This method is intuitive and easy to understand, particularly for beginners.
Prime Factorization
A more sophisticated approach utilizes the prime factorization of each number. This method requires breaking down each number into its prime factors: 10 = 2 x 5 and 25 = 5 x 5 (or 52).
The LCM is then found by taking the highest power of each prime factor present in either factorization: 21 x 52 = 2 x 25 = 50.
Prime factorization is especially useful when dealing with larger numbers or finding the LCM of multiple numbers simultaneously.
Using the Greatest Common Divisor (GCD)
The relationship between the LCM and the Greatest Common Divisor (GCD) provides another method for calculation. The GCD of 10 and 25 is 5. The LCM can be calculated using the formula: LCM(a, b) = (|a * b|) / GCD(a, b). Therefore, LCM(10, 25) = (10 * 25) / 5 = 250 / 5 = 50.
This method demonstrates the interconnectedness of different mathematical concepts.
Real-World Applications of the LCM
The LCM is not merely an abstract mathematical concept; it has numerous practical applications across a wide range of fields. These applications highlight the utility of the LCM in solving real-world problems.
Scheduling and Synchronization
One common application is in scheduling events or processes that occur at different intervals. Imagine two buses that depart from the same station. One bus leaves every 10 minutes and the other every 25 minutes.
The LCM of 10 and 25 (which is 50) tells us that the buses will depart together again after 50 minutes.
Fractions and Arithmetic Operations
The LCM is crucial when adding or subtracting fractions with different denominators. Finding a common denominator involves determining the LCM of the denominators.
For example, when adding 1/10 and 1/25, the LCM of 10 and 25 (50) is used as the common denominator, resulting in 5/50 + 2/50 = 7/50.
Gear Ratios and Mechanical Systems
In mechanical engineering, the LCM is used in determining gear ratios and analyzing the synchronization of rotating parts. Understanding the LCM helps engineers design efficient and harmonious mechanical systems.
This ensures that components function correctly and avoid unnecessary wear and tear.
The Importance of Understanding the LCM
Understanding the LCM is more than just memorizing a mathematical procedure. It fosters critical thinking, problem-solving skills, and a deeper appreciation for the interconnectedness of mathematical concepts.
A solid grasp of the LCM lays the foundation for more advanced topics in mathematics and science.
Conclusion: The Enduring Relevance of the LCM
The question of "What is the LCM of 10 and 25?" leads to a foundational answer with broad implications. Despite its relative simplicity, the LCM remains an indispensable tool across various disciplines, impacting our daily lives in ways both subtle and profound.
As technology advances and the complexity of our world increases, the fundamental principles of mathematics, including the LCM, will continue to be vital for innovation and progress.





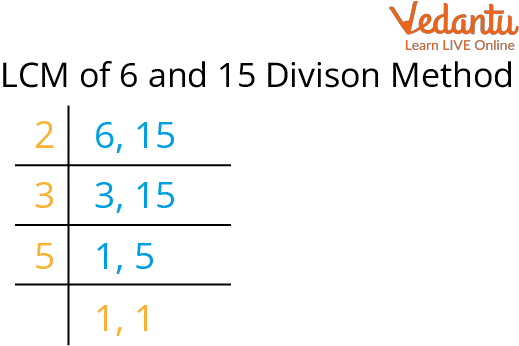





/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)



