What Is The Lcm Of 15 And 18

Imagine a bustling school fair, children darting between game booths, their laughter echoing in the air. Two friends, Maya and David, are planning a bake sale. Maya wants to bake cookies in batches of 15, while David is making cupcakes in batches of 18. They want to sell them in equal-sized packages, ensuring no cookies or cupcakes are left over. But how many treats should each package contain?
The answer lies in understanding a fundamental concept in mathematics: the Least Common Multiple (LCM). This article will unravel the mystery of the LCM, specifically focusing on finding the LCM of 15 and 18, and highlighting its relevance beyond simple arithmetic.
Understanding the Least Common Multiple
The LCM, as the name suggests, is the smallest number that is a multiple of two or more given numbers. It's a concept that crops up frequently in everyday life, from scheduling events to dividing resources fairly.
Think of it like this: you have two runners on a track. One completes a lap every 15 seconds, and the other every 18 seconds. The LCM will tell you when they'll both be at the starting line again, at the same time.
Methods for Finding the LCM of 15 and 18
There are several methods to determine the LCM, each with its own advantages.
Method 1: Listing Multiples
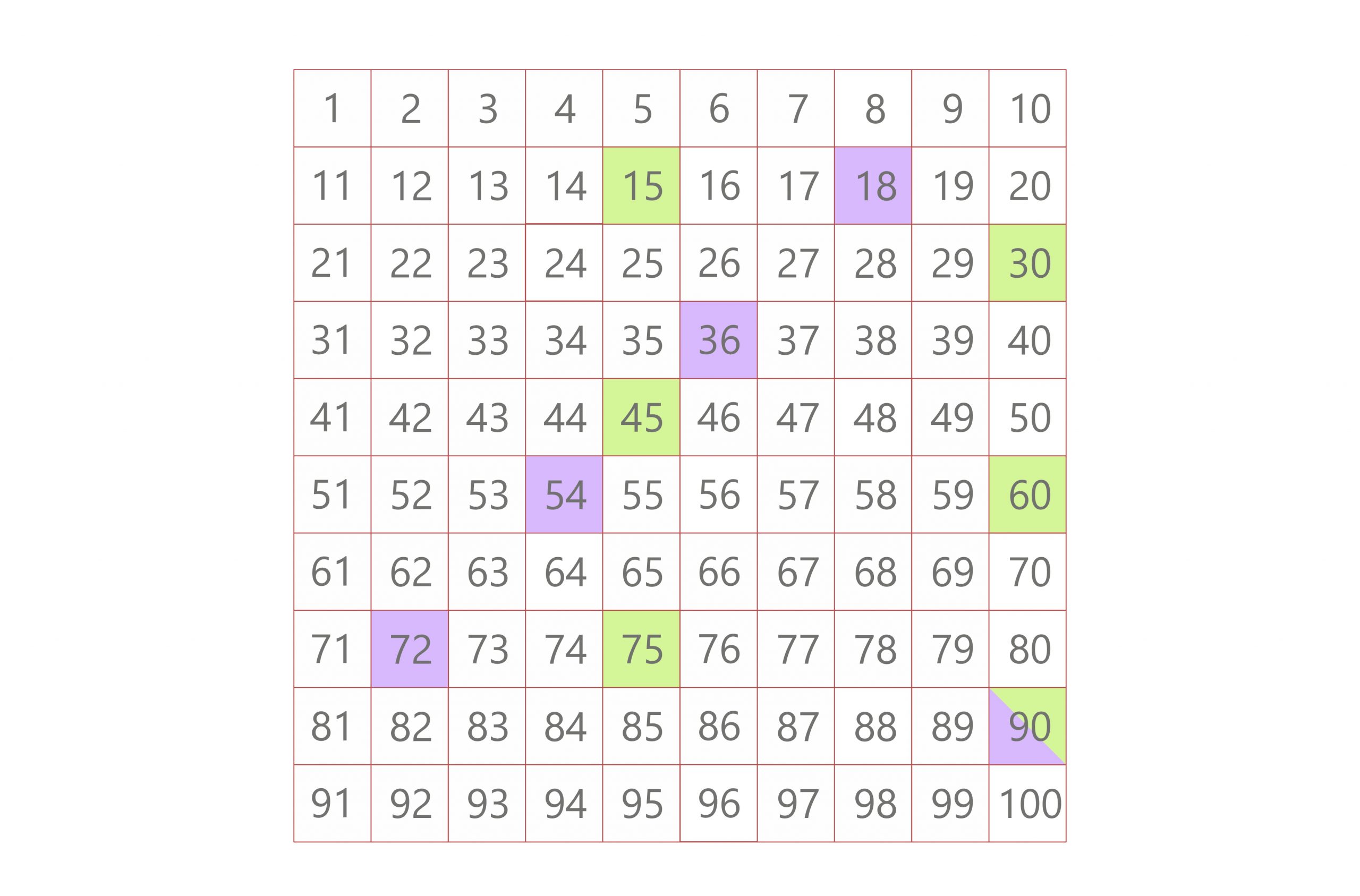
One straightforward approach is to list the multiples of each number until you find a common one. Multiples of 15 are: 15, 30, 45, 60, 75, 90, 105… Multiples of 18 are: 18, 36, 54, 72, 90, 108…
Notice that 90 appears in both lists. This is the smallest common multiple. Therefore, the LCM of 15 and 18 is 90.
Method 2: Prime Factorization
Prime factorization is a more efficient method, especially when dealing with larger numbers. It involves breaking down each number into its prime factors.
The prime factorization of 15 is 3 x 5. The prime factorization of 18 is 2 x 3 x 3 (or 2 x 32).
To find the LCM, we take the highest power of each prime factor that appears in either factorization. We have 21, 32, and 51. Multiplying these together: 2 x 9 x 5 = 90.
Method 3: Using the Greatest Common Divisor (GCD)
The GCD, or Greatest Common Divisor, is the largest number that divides evenly into two or more numbers. The GCD of 15 and 18 is 3.
There's a handy formula that relates the LCM and GCD: LCM(a, b) = (a x b) / GCD(a, b). Applying this to our numbers: LCM(15, 18) = (15 x 18) / 3 = 270 / 3 = 90.
Real-World Applications of LCM
Understanding the LCM isn't just an academic exercise; it has practical applications in various fields.
In scheduling, the LCM can help determine when events will coincide. Imagine two buses leaving a station at different intervals; the LCM will tell you when they'll both be at the station simultaneously again.
In cooking and baking, the LCM can assist in scaling recipes. If you need to adjust a recipe that calls for ingredients in different units, the LCM can ensure you maintain the correct proportions.
In music, the LCM helps understand rhythmic patterns and synchronization. The timing of different musical phrases can be analyzed using LCM to find the point where they align.
Returning to Maya and David's Bake Sale
So, back to our initial scenario: Maya and David. They've determined the LCM of 15 and 18 is 90. This means they can create 90/15 = 6 packages of cookies and 90/18 = 5 packages of cupcakes.
However, that means they would have only 5 packages of cupcakes and 6 packages of cookies. This is not the answer. If they want to create equal packages, each package must contain the same ratio of cookies and cupcakes.
This is why the LCM is useful. They want the smallest number of total baked goods (both cookies and cupcakes) that is divisible by both 15 and 18. This is 90. But they need to have the same number of cookies and cupcakes. To do this, David needs to bake enough cupcakes to make 6 batches of cupcakes. The number of cupcakes needed is 6 * 18 = 108. Maya needs to bake enough cookies to make 5 batches of cookies. The number of cookies needed is 5 * 15 = 75. The total number of baked goods is 108 + 75 = 183. The LCM of 15 and 18 cannot be used directly here.
Maya and David can create 3 packages. Each package would have 25 cookies and 36 cupcakes.
For equal-sized packages with no leftovers, they need to find a number that is divisible by both 15 and 18, and then determine the number of cookies and cupcakes to bake to achieve that multiple. They cannot directly find the answer with the LCM.
The Beauty of Mathematical Concepts
The LCM, often presented as a dry mathematical concept, reveals its beauty when applied to real-world situations. It empowers us to solve problems efficiently and make informed decisions.
From organizing bake sales to managing complex schedules, the LCM provides a framework for understanding and optimizing various aspects of our lives. It demonstrates the interconnectedness of mathematical principles and their relevance in our daily experiences.
As we navigate the world around us, remembering the power of the LCM can unlock new perspectives and simplify complex challenges. It's a testament to the elegance and practicality of mathematics, reminding us that even seemingly abstract concepts can have profound impacts on our lives.












/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)


