What Is The Lcm Of 18 And 27

In classrooms across the nation, a silent struggle unfolds daily: the battle against mathematical concepts that seem simple on the surface but harbor surprising depth. One such battleground centers on the Least Common Multiple, or LCM, and particularly, the LCM of seemingly straightforward numbers like 18 and 27. Understanding this concept is not just an academic exercise; it's a gateway to more complex mathematical understanding.
This article delves into the calculation and understanding of the LCM of 18 and 27. It will explore the various methods for determining this value, its applications in real-world scenarios, and why it remains a crucial concept in foundational mathematics. We'll examine prime factorization, listing multiples, and the division method to illuminate the process. Furthermore, we will explore the relationship between LCM and Greatest Common Divisor (GCD).
Defining the Least Common Multiple
The LCM, or Least Common Multiple, of two or more numbers is the smallest positive integer that is divisible by all of the given numbers. It's a fundamental concept in number theory, often used when working with fractions, ratios, and various problem-solving scenarios. Understanding LCM is crucial for students progressing through arithmetic and algebra.
For example, when adding or subtracting fractions with different denominators, finding the LCM of those denominators is essential for establishing a common denominator. This allows for seamless calculations and accurate results.
Methods for Finding the LCM of 18 and 27
Several methods exist for calculating the LCM. Here are three commonly used techniques, applied specifically to the numbers 18 and 27.
Method 1: Listing Multiples
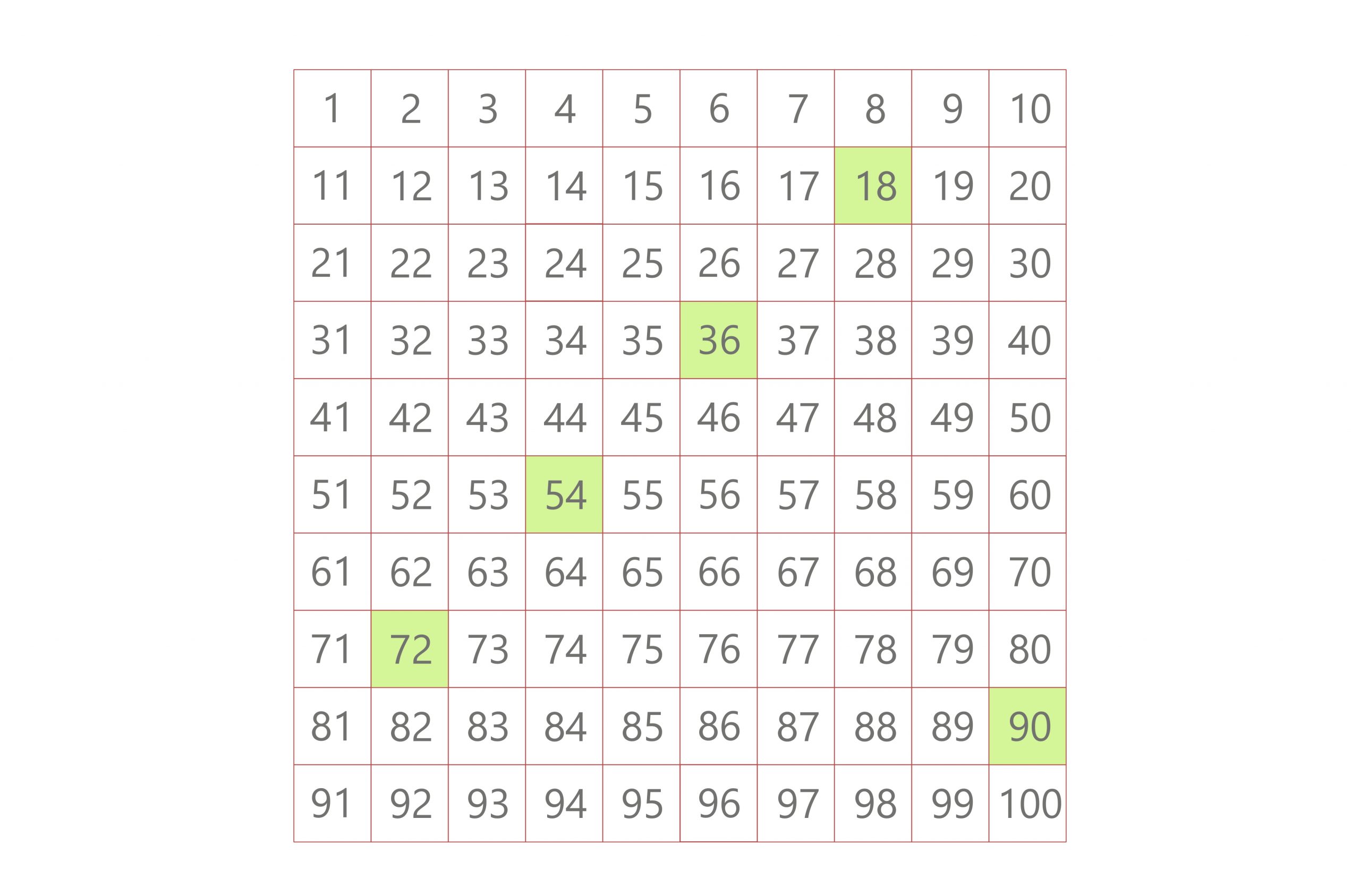
This method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Multiples of 18: 18, 36, 54, 72, 90...
Multiples of 27: 27, 54, 81, 108...
As you can see, 54 appears in both lists. Therefore, the LCM of 18 and 27 is 54.
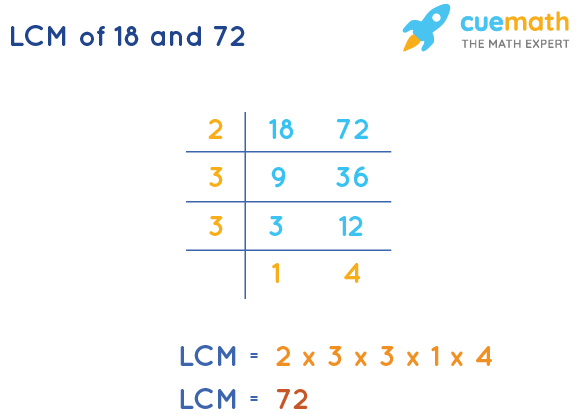
Method 2: Prime Factorization
Prime factorization involves breaking down each number into its prime factors. The LCM is then calculated by taking the highest power of each prime factor that appears in either number's factorization.
The prime factorization of 18 is 2 x 3 x 3, or 2 x 32.
The prime factorization of 27 is 3 x 3 x 3, or 33.
To find the LCM, we take the highest power of each prime factor: 21 and 33. Multiplying these together, we get 2 x 27 = 54. Thus, the LCM of 18 and 27 is 54.
Method 3: Division Method
This method involves dividing both numbers by their common prime factors until both numbers are reduced to 1. The LCM is the product of all the divisors used.
Divide 18 and 27 by their common factor, 3: 18/3 = 6, 27/3 = 9.
Divide 6 and 9 by their common factor, 3: 6/3 = 2, 9/3 = 3.
Now divide 2 by 2: 2/2 = 1. Divide 3 by 3: 3/3 = 1.
The divisors were 3, 3, 2, and 3. Multiplying these together: 3 x 3 x 2 x 1 = 54.
Oops, the previous calculation made a mistake. The correct calculation is to multiply the divisors used to reduce both numbers to 1: 3 x 3 x 2 = 18. Then multiply by the last remaining number, 3: 18 x 3 = 54. The LCM of 18 and 27 is 54.
The Relationship Between LCM and GCD
The LCM and GCD (Greatest Common Divisor) are closely related. The product of two numbers is equal to the product of their LCM and GCD.
In the case of 18 and 27, the GCD is 9 (the largest number that divides both 18 and 27 without a remainder). Therefore, 18 x 27 = LCM(18, 27) x GCD(18, 27), which is 486 = LCM(18, 27) x 9.
Solving for the LCM, we get LCM(18, 27) = 486 / 9 = 54. This confirms our previous calculations.
Real-World Applications of LCM
Understanding LCM extends beyond the classroom, influencing problem-solving in practical situations. For example, LCM is crucial in scheduling repetitive events. If one task happens every 18 minutes and another happens every 27 minutes, the LCM tells you when they'll coincide.
LCM is also used in manufacturing and engineering, particularly when synchronizing different processes. It ensures smooth operations and efficient resource allocation.
Educational Significance
The LCM is a cornerstone of mathematical education. Mastery of this concept sets the stage for success in algebra, calculus, and more advanced mathematical studies.
Teachers emphasize LCM to foster critical thinking and problem-solving skills. Students who understand LCM are better equipped to tackle complex mathematical challenges.
Conclusion
Calculating the LCM of 18 and 27 is not merely an arithmetic exercise; it's a demonstration of fundamental mathematical principles with wide-ranging applications. Whether listing multiples, using prime factorization, or employing the division method, understanding these approaches provides a solid foundation for mathematical proficiency. As educators continue to emphasize the importance of foundational concepts like LCM, future generations will be better equipped to navigate the complexities of mathematics and the world around them.









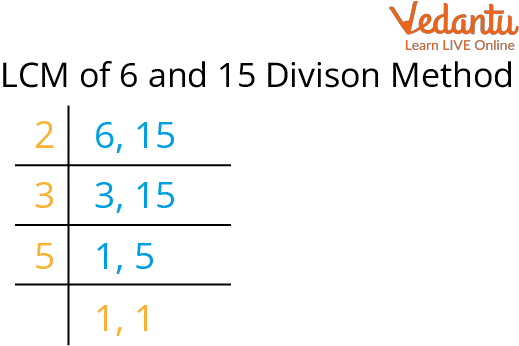

/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)