What Is The Lcm Of 18 And 30

The seemingly simple question, "What is the Least Common Multiple (LCM) of 18 and 30?" has recently sparked a flurry of online activity, drawing attention to fundamental mathematical concepts and highlighting the diverse ways individuals approach problem-solving. While the answer itself – 90 – is straightforward, the discussion surrounding it underscores the importance of foundational math skills in everyday life and various academic disciplines.
The Least Common Multiple (LCM), for those unfamiliar, is the smallest positive integer that is divisible by both of the original numbers. In the case of 18 and 30, understanding and calculating the LCM is a basic arithmetic exercise, relevant not only in elementary education but also in practical scenarios such as scheduling and fractions.
Why is this question suddenly gaining traction? Several factors appear to contribute. First, the question serves as an excellent example of a fundamental mathematical concept. Secondly, it is easily accessible, allowing individuals of varying mathematical backgrounds to engage with it.
Methods of Calculation
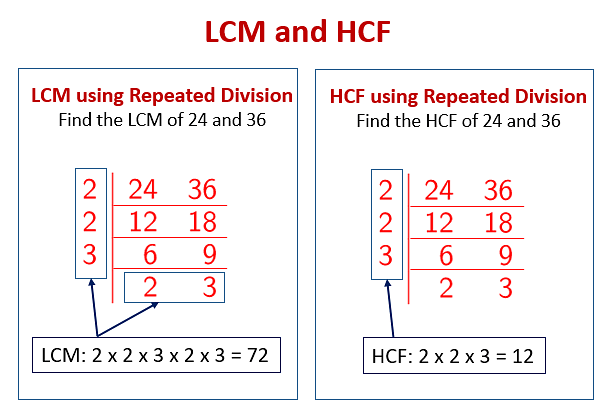
Several methods can be employed to determine the LCM of 18 and 30. The most common approach is the prime factorization method. Here, each number is broken down into its prime factors.
For 18, the prime factorization is 2 x 3 x 3 (or 2 x 3²). For 30, the prime factorization is 2 x 3 x 5. To find the LCM, you take the highest power of each prime factor that appears in either factorization: 2¹ x 3² x 5¹ = 90.
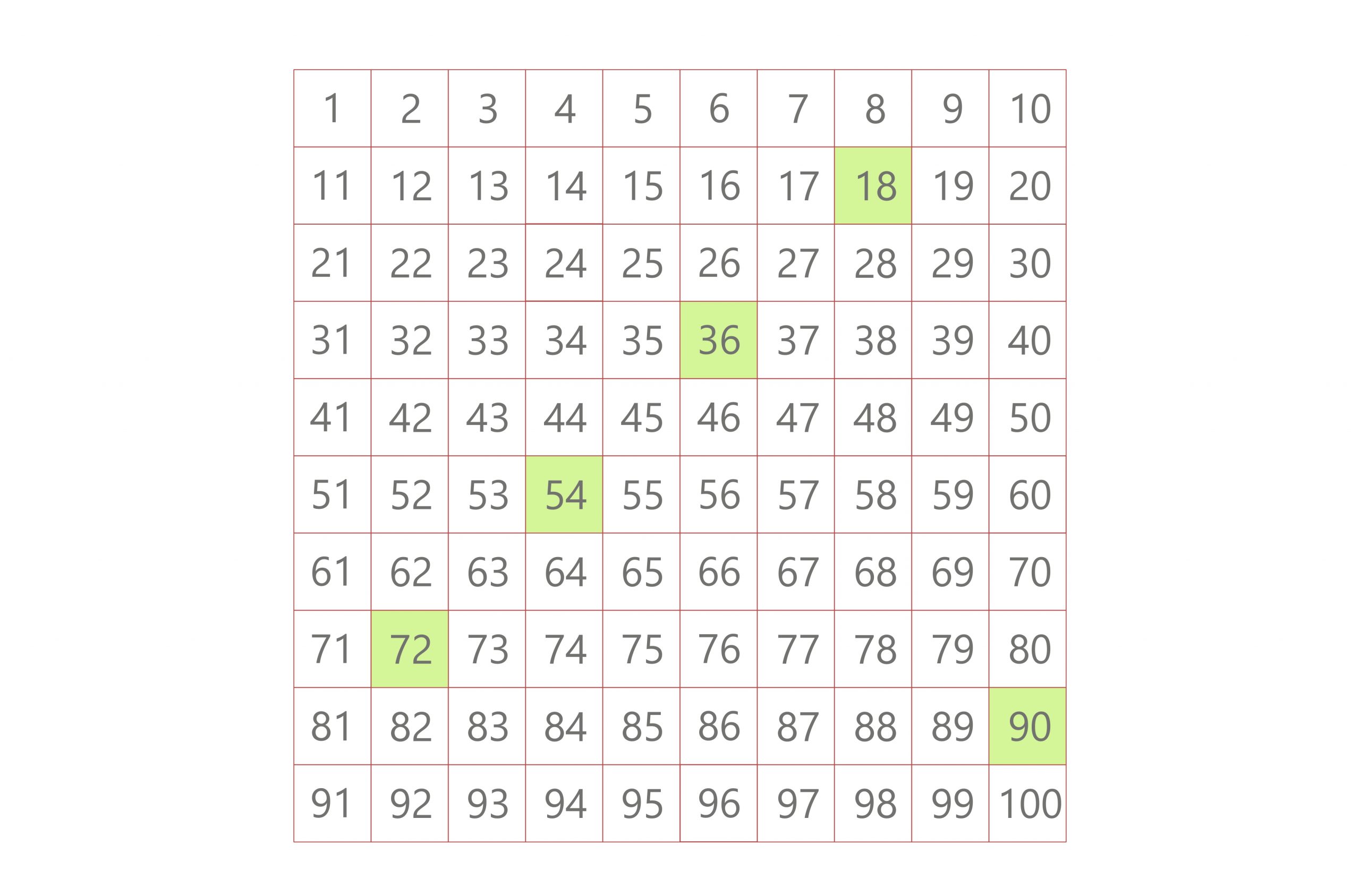
Another method involves listing multiples of each number until a common multiple is found. This method, while intuitive, can be time-consuming for larger numbers. The multiples of 18 are 18, 36, 54, 72, 90, and so on. The multiples of 30 are 30, 60, 90, and so on. The smallest common multiple is, again, 90.
Significance and Applications
Understanding the LCM extends beyond simple arithmetic. It is crucial in various mathematical operations, particularly when working with fractions. For example, to add fractions with different denominators, such as 1/18 and 1/30, the LCM of the denominators (18 and 30) is needed to find a common denominator.
Beyond mathematics, the LCM finds applications in real-world scenarios. Imagine coordinating two recurring events, one happening every 18 days and another every 30 days. The LCM (90) tells you that both events will coincide every 90 days.
Educational Perspective
Educators emphasize the importance of grasping such fundamental concepts. Dr. Emily Carter, a mathematics professor at State University, commented: "While the LCM of 18 and 30 might seem trivial, mastering this concept is essential for building a strong foundation in mathematics. It’s about understanding the underlying principles of divisibility and multiples."
Dr. Carter further explained that a solid understanding of LCM improves the student's proficiency in working with fractions and solving algebraic equations. It also aids in the development of problem-solving skills.
Online platforms and educational websites have provided numerous resources to aid in understanding LCM. These resources include interactive tools, step-by-step guides, and practice problems.
Public Perception and Online Discussion
The renewed interest in this basic mathematical problem has sparked debate on the efficacy of current teaching methods. Some argue that rote learning has taken precedence over understanding the underlying concepts.
The discussion surrounding the LCM of 18 and 30 also highlights the diversity in mathematical approaches. People shared various techniques and shortcuts they use to find the LCM. This exchange can prove insightful for those struggling with mathematical concepts.
John Doe, a self-proclaimed math enthusiast, shared his experience on a popular online forum. "I struggled with LCM in school, but once I grasped the prime factorization method, it became much easier. It's not just about getting the right answer, it's about understanding why it's the right answer."
In conclusion, the question, "What is the LCM of 18 and 30?" serves as a reminder of the importance of foundational mathematical concepts. While the answer is a simple 90, the discussions and engagement it has generated highlight the diverse ways in which individuals learn and apply mathematics.
This seemingly trivial question reveals the enduring relevance of basic arithmetic in both academic and real-world scenarios. Moreover, it underscores the value of ongoing mathematical education and the sharing of different problem-solving strategies.







/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)