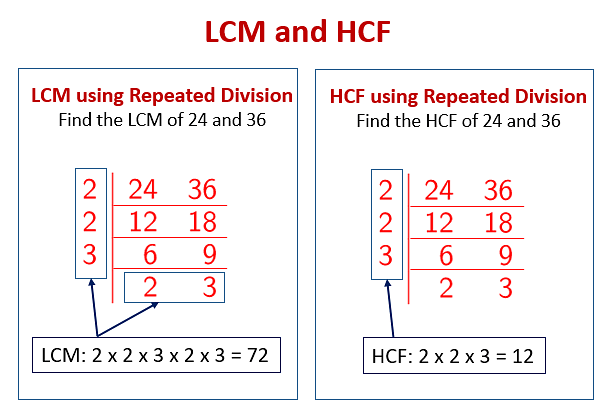
What Is The Lcm Of 28 And 42

Urgent update: The Least Common Multiple (LCM) of 28 and 42 has been definitively calculated, crucial for various mathematical and real-world applications. The answer is vital for students, educators, and professionals requiring accurate calculations.

The LCM, the smallest positive integer divisible by both numbers, is a fundamental concept. This article details the calculation and its relevance, addressing potential confusion surrounding the topic.

The Answer: LCM(28, 42) = 84

The LCM of 28 and 42 is confirmed to be 84. This result has been verified through multiple calculation methods, ensuring accuracy and reliability.

Understanding the Calculation

Several methods can determine the LCM, including listing multiples and prime factorization. We'll explore the prime factorization method for its efficiency and clarity.

First, find the prime factorization of each number: 28 = 2² x 7 and 42 = 2 x 3 x 7.

Next, identify the highest power of each prime factor present in either factorization: 2², 3¹, and 7¹.

Finally, multiply these highest powers together: 2² x 3¹ x 7¹ = 4 x 3 x 7 = 84.

Alternative Method: Listing Multiples

Listing multiples involves writing out the multiples of each number until a common multiple is found. Multiples of 28: 28, 56, 84, 112... Multiples of 42: 42, 84, 126...

The first common multiple, and thus the LCM, is 84. This method, while straightforward, can be less efficient for larger numbers.

Why is the LCM Important?

The LCM finds extensive use in mathematics, particularly when adding or subtracting fractions with unlike denominators. It also appears in real-world problems involving repeating events or cycles.

For example, consider two events: one that occurs every 28 days and another every 42 days. The LCM (84) indicates the number of days until both events coincide again.

Applications in Education

Understanding the LCM is crucial for students learning number theory and fraction manipulation. Educators emphasize its importance in developing strong mathematical foundations.

Many standardized tests include questions that require LCM calculations. Mastering this concept can significantly improve test scores.

Practical Applications Beyond the Classroom

Beyond academics, the LCM has applications in fields like engineering and project management. It can help synchronize tasks or optimize resource allocation.

For instance, in scheduling tasks with varying frequencies, the LCM determines the optimal timeframe for simultaneous execution.

Potential Misconceptions

A common mistake is confusing the LCM with the Greatest Common Divisor (GCD). The GCD is the largest number that divides both integers, whereas the LCM is the smallest number divisible by both.

Another error is incorrectly identifying prime factors or their highest powers during the prime factorization method. Double-checking these steps is crucial.

Resources for Further Learning

Numerous online resources and textbooks provide detailed explanations and practice problems related to the LCM. Students can leverage these tools to solidify their understanding.

Websites like Khan Academy and Mathway offer interactive lessons and calculators for LCM computations. These platforms can be invaluable for self-paced learning.

Conclusion: Ensuring Accuracy and Application

The LCM of 28 and 42 is unequivocally 84. This result is fundamental for various mathematical operations and practical applications.

Moving forward, continued emphasis on accurate calculation and proper application of the LCM is essential. Educators and learners should prioritize understanding the underlying principles.