What Is The Lcm Of 42 And 28

Imagine a bustling farmer's market on a sunny Saturday morning. Baskets overflow with vibrant fruits and vegetables, and the air is filled with the cheerful chatter of vendors and customers. Amidst this lively scene, a young apprentice baker named Leo is carefully arranging rows of perfectly crafted muffins and croissants. He’s preparing for a special order, one that requires him to understand a fundamental concept in mathematics: the Least Common Multiple, or LCM.
This brings us to a seemingly simple question: What is the LCM of 42 and 28? The answer, 84, is more than just a number; it's a cornerstone of arithmetic with practical applications in everyday life, from scheduling events to managing resources efficiently.
At its core, the LCM is the smallest positive integer that is perfectly divisible by two or more numbers. Finding the LCM of 42 and 28 allows us to understand how these numbers interact and find a common ground for calculations, problem-solving, and more.
Understanding the Fundamentals
To truly appreciate the LCM of 42 and 28, we need to delve into the world of factors and multiples. Let's start with a definition: A factor of a number divides it evenly, leaving no remainder.
For example, the factors of 42 are 1, 2, 3, 6, 7, 14, 21, and 42. Similarly, the factors of 28 are 1, 2, 4, 7, 14, and 28.
Now, consider multiples. A multiple of a number is simply the result of multiplying that number by any integer. So, multiples of 42 include 42, 84, 126, 168, and so on.
For 28, the multiples are 28, 56, 84, 112, 140, and so on. The LCM, therefore, is the smallest number that appears in both lists of multiples.
Methods to Calculate the LCM
Several methods exist to calculate the LCM, each with its own merits. One of the most straightforward is the listing method. You list out multiples of each number until you find a common one.
As demonstrated above, listing multiples of 42 and 28 shows that 84 is the smallest common multiple. This method is intuitive and easy to understand, especially for smaller numbers.
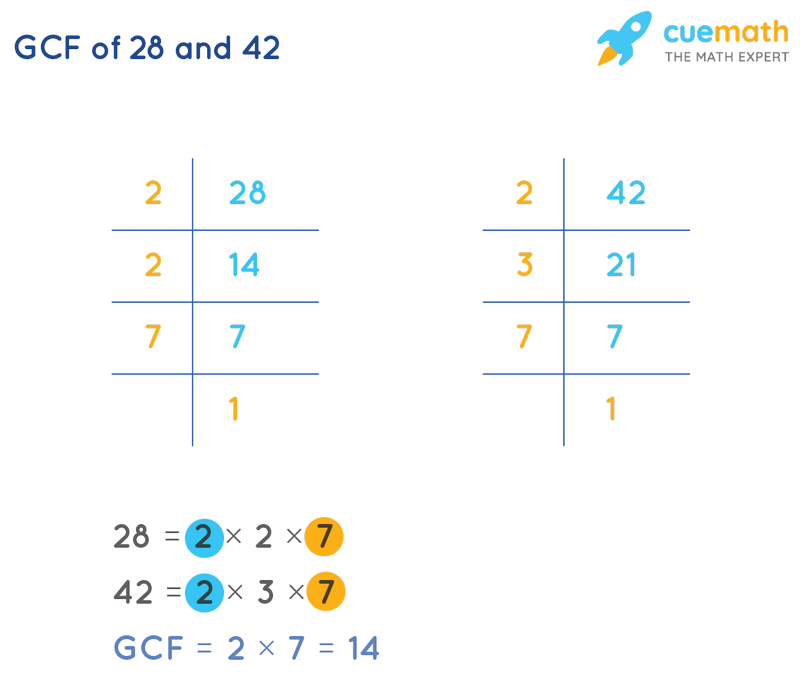
Another popular method involves prime factorization. This technique breaks down each number into its prime factors. The prime factors of 42 are 2 x 3 x 7, and the prime factors of 28 are 2 x 2 x 7 (or 2² x 7).
To find the LCM using prime factorization, take the highest power of each prime factor that appears in either factorization. In this case, we have 2², 3, and 7. Multiply these together: 2² x 3 x 7 = 4 x 3 x 7 = 84.
Finally, we can also use the Greatest Common Divisor (GCD) to find the LCM. The GCD is the largest number that divides evenly into two or more numbers.
The GCD of 42 and 28 is 14. The formula to find the LCM using the GCD is: LCM(a, b) = (a x b) / GCD(a, b).
Applying this formula, LCM(42, 28) = (42 x 28) / 14 = 1176 / 14 = 84. Regardless of the method used, the LCM of 42 and 28 consistently comes out to be 84.
Real-World Applications
The LCM isn't just a theoretical concept; it has numerous practical applications in various fields. In everyday life, it's used in scheduling and organizing events.
Imagine Leo, the baker from our opening scene, needs to bake muffins and croissants for a large order. If the muffins take 42 minutes to bake and the croissants take 28 minutes, finding the LCM (84 minutes) helps him determine the shortest amount of time needed to have both batches ready simultaneously.
In mathematics, the LCM is crucial when working with fractions. To add or subtract fractions with different denominators, you need to find a common denominator, and the LCM of the denominators is often the easiest choice.
Consider adding 1/42 and 1/28. The LCM of 42 and 28 is 84, so we can rewrite the fractions as 2/84 and 3/84. This makes the addition straightforward: 2/84 + 3/84 = 5/84.
In computer science, the LCM is used in tasks such as scheduling processes and allocating resources. The efficient management of time and resources often relies on finding common multiples.
Even in music, the LCM can be used to understand rhythmic patterns. If one rhythm repeats every 42 beats and another repeats every 28 beats, the LCM (84) indicates how many beats it will take for the two rhythms to align again.
Why This Matters
Understanding the LCM is more than just memorizing a formula; it's about developing critical thinking and problem-solving skills. This concept highlights the interconnectedness of numbers and their applications in real-world situations.
From baking schedules to fraction calculations, the LCM provides a framework for solving problems efficiently. It demonstrates the elegance and practicality of mathematics in our daily lives.
Moreover, mastering the LCM lays a strong foundation for more advanced mathematical concepts. It's a stepping stone to understanding more complex topics in algebra, calculus, and beyond.
A Final Thought
The LCM of 42 and 28, which is 84, represents more than just a number. It embodies a powerful mathematical concept with far-reaching implications.
Whether you're a baker scheduling baking times, a student tackling fractions, or a computer scientist managing resources, the LCM provides a valuable tool for solving problems and optimizing processes. The ability to find the LCM and understand its significance is a valuable skill.
So, the next time you encounter the LCM, remember Leo at the farmer's market. Remember the meticulous calculations, and remember the real-world impact of this seemingly simple concept. Mathematics, after all, is woven into the fabric of our daily lives, making the world around us a little easier to understand.








/Activities/Guide62_LeastCommonMultiple-Example-1_v1.png)