What Is The Total Area Of The Figure Below

A deceptively simple geometric problem, asking for the total area of a figure composed of squares and rectangles, has sparked widespread discussion online and in classrooms across the nation. The problem, often presented visually with a figure composed of interconnected shapes, has proven to be more challenging than it initially appears.
The question centers on determining the combined area of a composite figure. This figure includes several squares and rectangles of varying, but clearly defined, dimensions. Accuracy hinges on careful measurements and strategic application of basic geometric formulas.
The Challenge Defined
The "figure," typically displayed as an image alongside the area question, is the core of the problem. It consists of a collection of rectangles and squares. These figures are arranged adjacently or overlapping to form a larger, more complex shape.
The key details provided usually include the lengths of some sides. Some side lengths might be inferred via relationships of adjacent sides. These relationships are either presented directly or can be deduced from the visual representation of the figure.
Solving the Puzzle: A Step-by-Step Approach
To accurately calculate the total area, several steps must be meticulously followed. First, identify all individual rectangles and squares. This can be achieved by carefully examining the figure and identifying its constituent shapes.
Next, determine the length and width of each individual shape. Known side lengths will be directly available, while others must be inferred. Use given relationships and visual cues to logically deduce the missing dimensions.
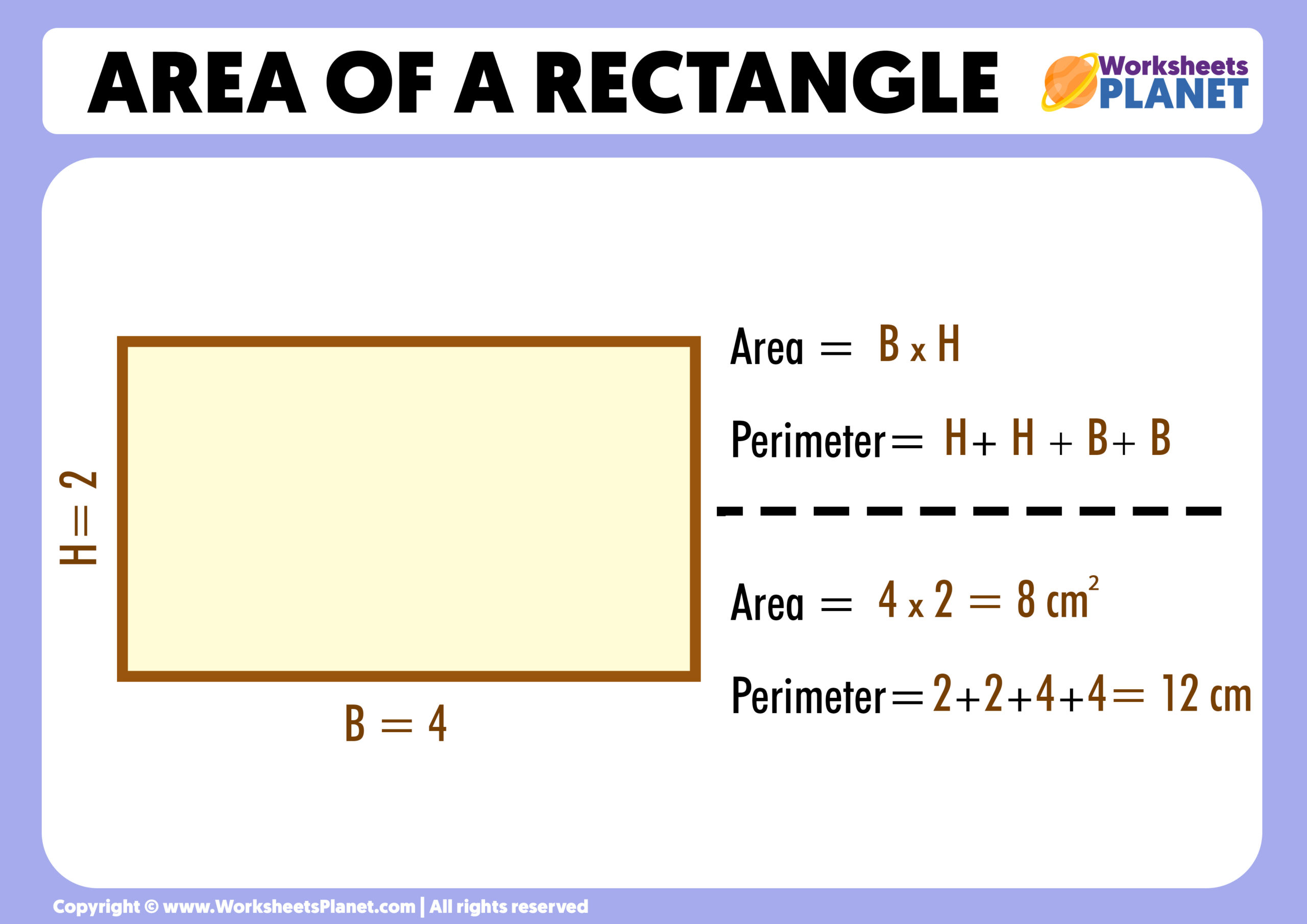
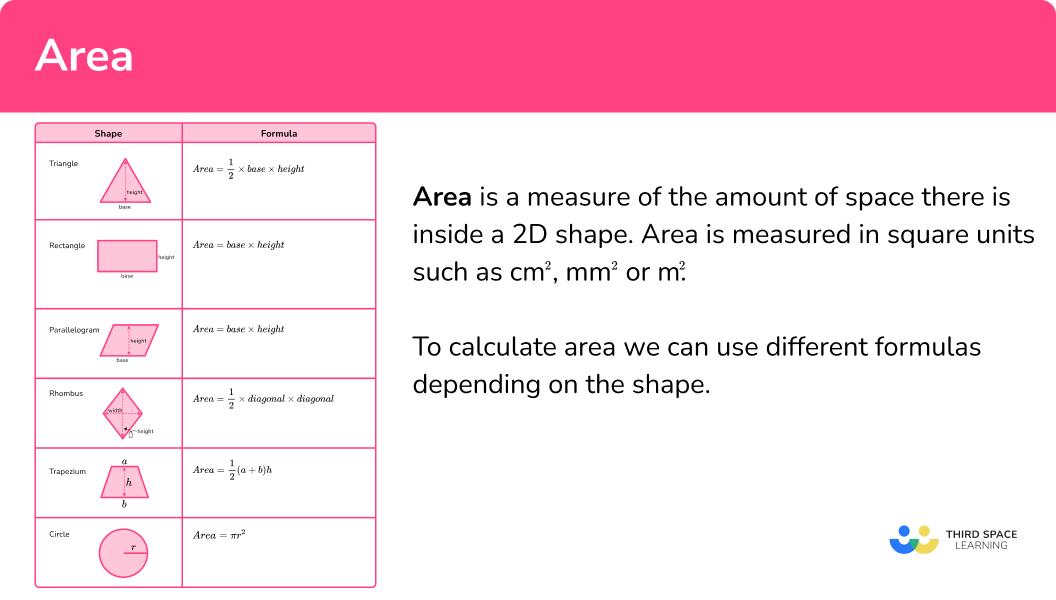
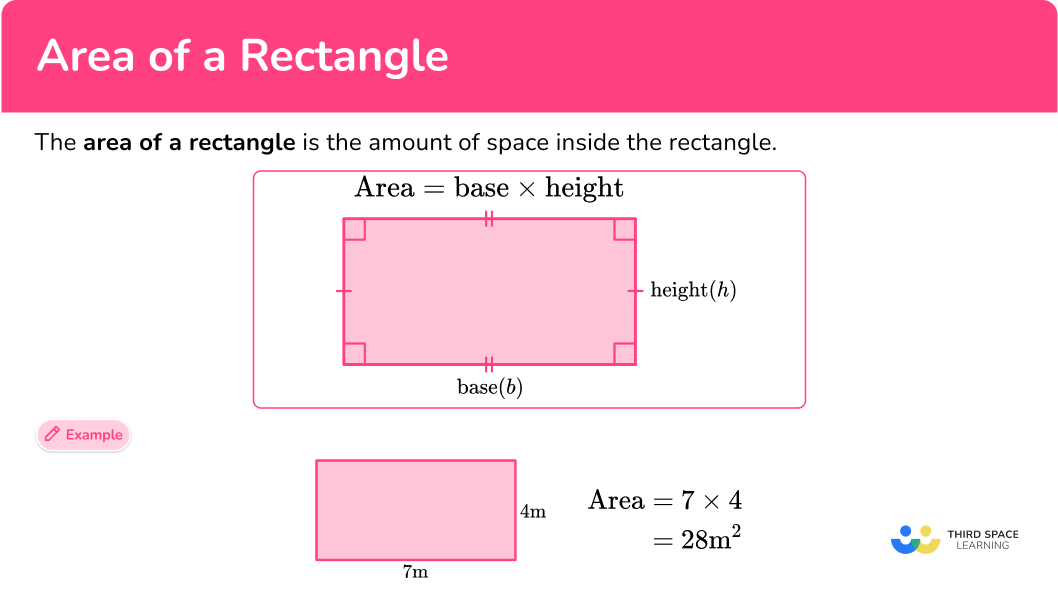
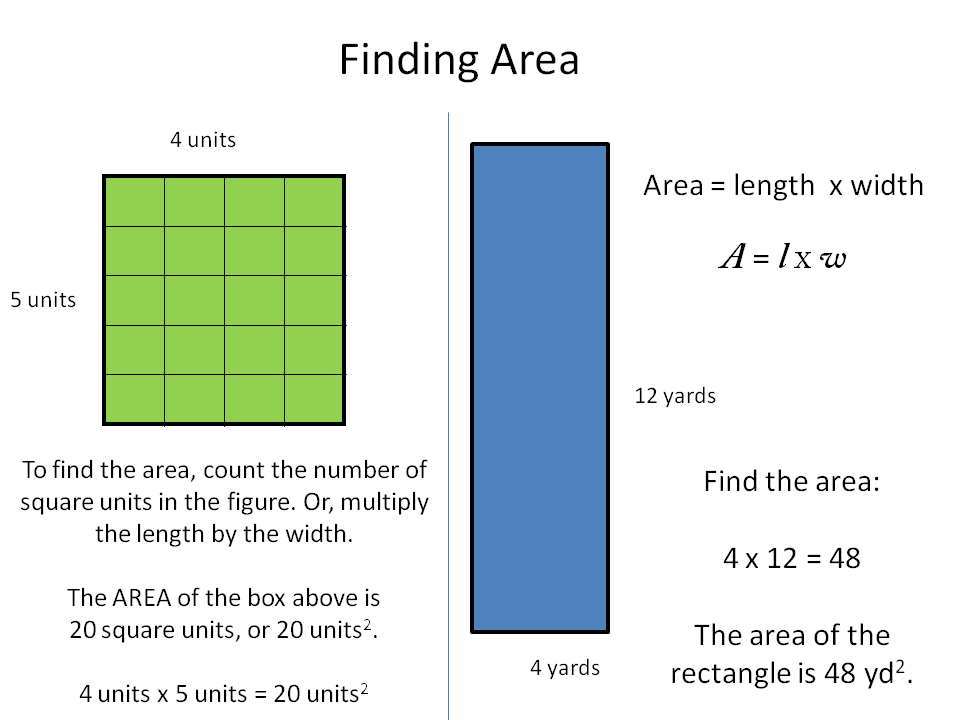
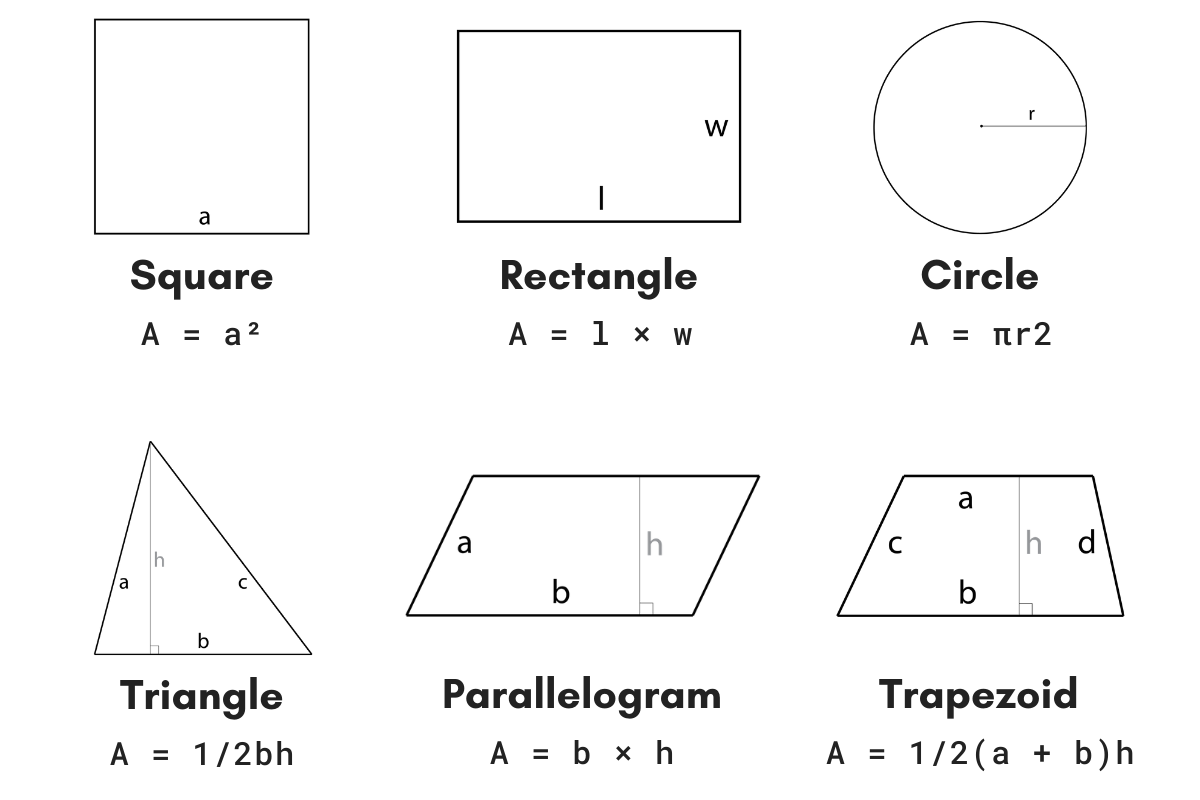
Calculate the area of each rectangle and square by multiplying the length by the width (Area = Length x Width). For instance, if a rectangle has a length of 5 cm and a width of 3 cm, its area would be 15 square centimeters.
Sum the areas of all the individual rectangles and squares. If the figure consists of shapes A, B, and C, with areas of 10, 15, and 20 square units respectively, the total area is 10 + 15 + 20 = 45 square units.
Pay close attention to overlapping regions. Subtract any overlapping areas from the total sum. Failure to do so will lead to an overestimation of the overall area.
Significance and Impact
Such geometric problems are more than just academic exercises. They play a crucial role in developing critical thinking and problem-solving skills. These skills are important in various fields, from engineering and architecture to everyday tasks like home improvement and design.
This particular area problem also highlights the importance of visual literacy and spatial reasoning. These skills are vital in interpreting diagrams, maps, and other visual representations of information.
The engagement with this problem extends beyond the classroom. Many people share solutions and strategies online. This creates a collaborative learning environment for tackling challenging geometric concepts.
Challenges and Common Mistakes
One of the most common mistakes is the failure to accurately identify all the individual shapes. This often occurs when complex figures are presented. It involves multiple overlapping or intersecting shapes.
Another frequent error lies in incorrectly calculating the area of individual shapes. This can happen due to misidentification of side lengths. Using the wrong formula can also lead to calculation errors.
Ignoring or miscalculating overlapping areas is a prevalent mistake. The oversight is a sure way to inflate the total calculated area.
Conclusion
The total area question is not just about numbers. It is about fostering geometric understanding. The question develops meticulous problem-solving skills. The figure exemplifies the value of accuracy and attention to detail.
By meticulously following the steps outlined above, individuals can confidently tackle similar geometric challenges. More importantly, individuals can develop a deeper appreciation for the power of visual reasoning and spatial analysis.