What Will Reduce The Width Of A Confidence Interval

In a world awash with data, the ability to make accurate and reliable inferences is more crucial than ever. From predicting election outcomes to assessing the efficacy of new drugs, confidence intervals provide a range within which the true value of a population parameter is likely to lie. But the width of these intervals – the degree of uncertainty they represent – can vary dramatically, impacting the usefulness of the insights derived.

Understanding how to narrow a confidence interval is paramount for researchers, policymakers, and anyone who relies on statistical analysis to make informed decisions. A narrower interval signifies greater precision and reduces the risk of drawing incorrect conclusions. It allows for more targeted interventions, more accurate predictions, and a clearer understanding of the underlying phenomena being studied.

This article delves into the key factors that influence the width of a confidence interval, exploring how sample size, variability, and confidence level each play a critical role in shaping the precision of our statistical estimates. We will examine the statistical principles at play, drawing on expert insights and real-world examples to illustrate how these factors can be strategically manipulated to achieve more meaningful results.

Understanding Confidence Intervals

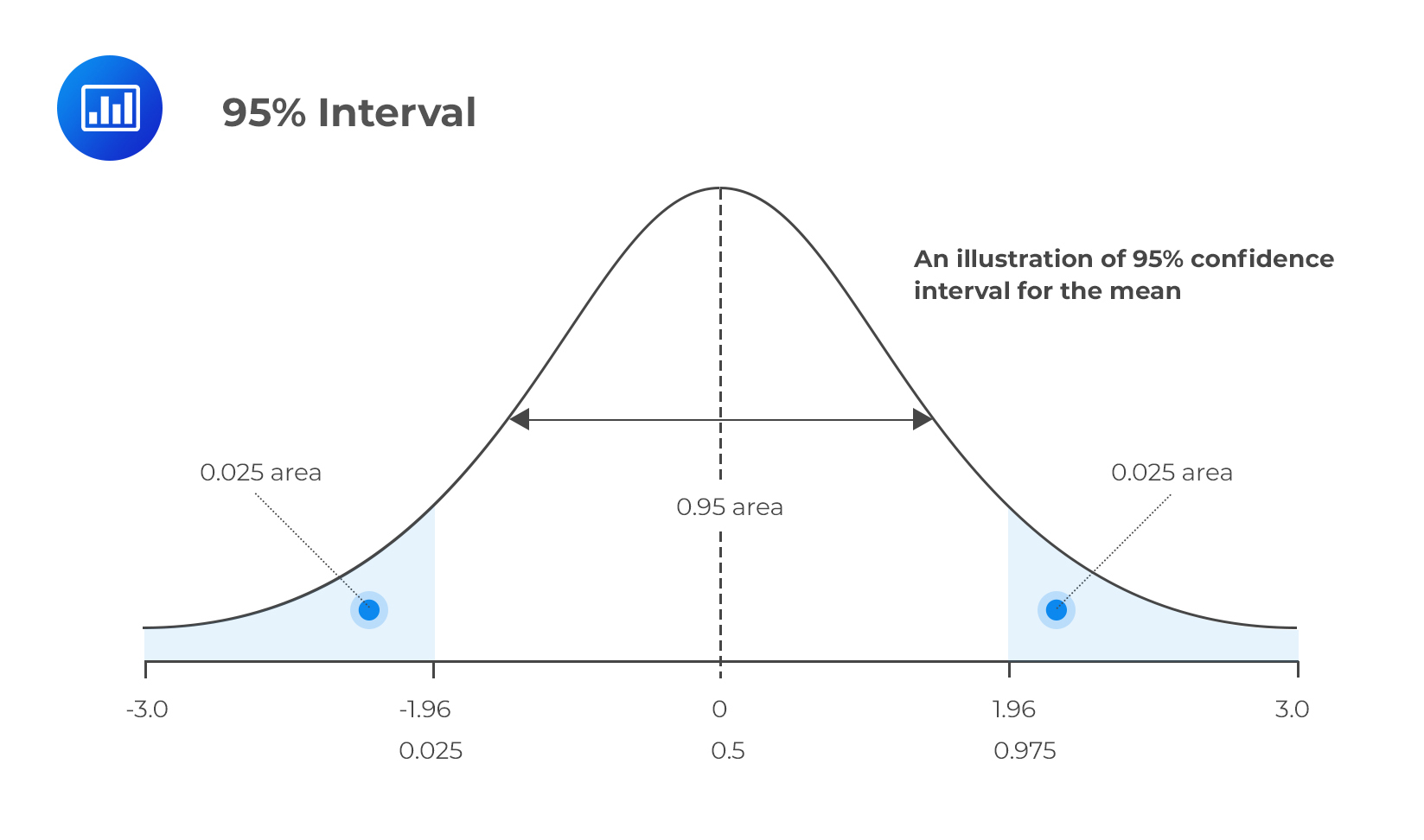
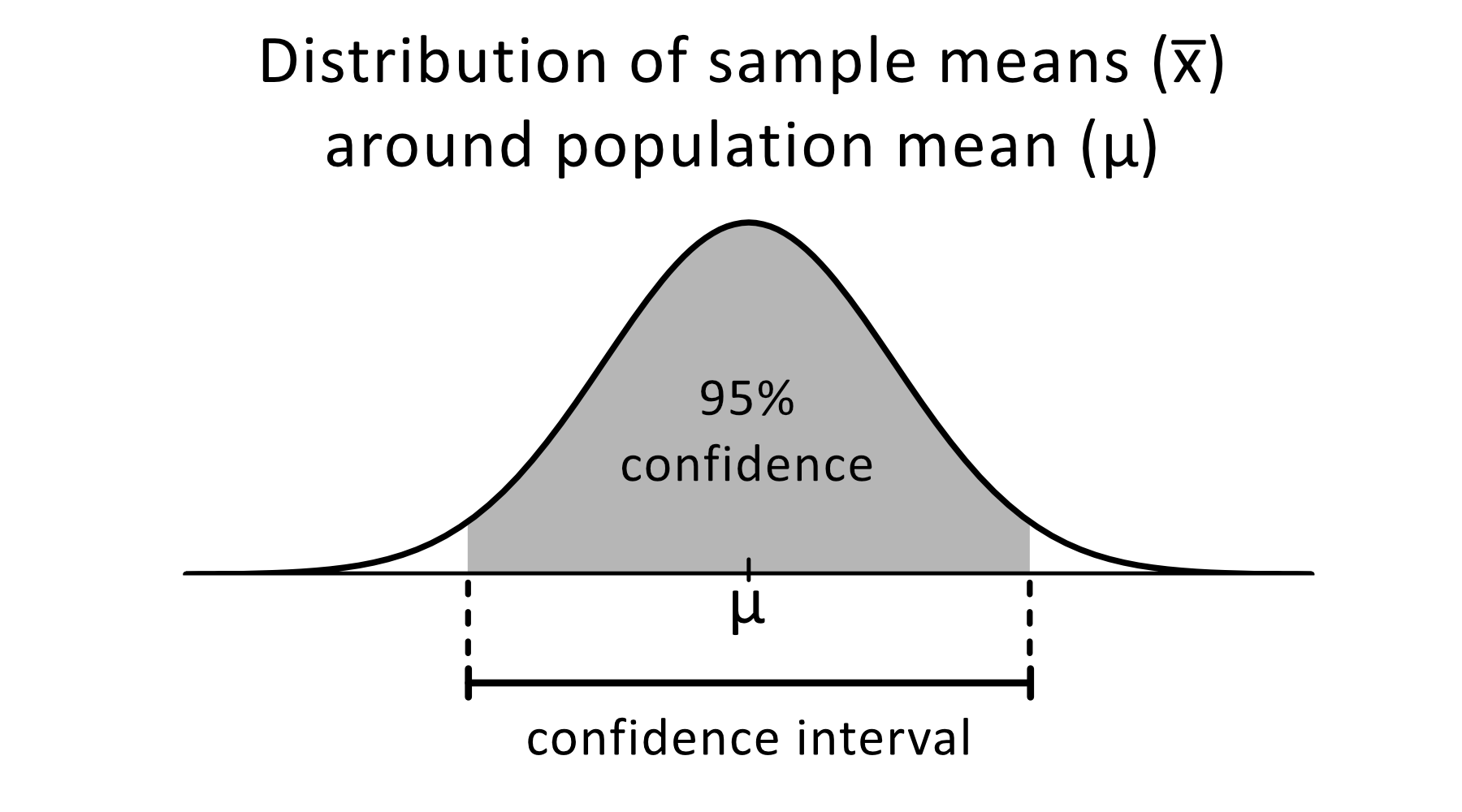
A confidence interval is a range of values calculated from sample data that is likely to contain the true population parameter with a certain degree of confidence. This confidence level, usually expressed as a percentage (e.g., 95% confidence), indicates the probability that the interval will capture the true value if the sampling process is repeated multiple times.

The width of the interval directly reflects the uncertainty associated with the estimate. A wider interval suggests greater uncertainty, while a narrower interval implies more precision. The goal is always to minimize this width while maintaining the desired level of confidence.

The Impact of Sample Size

One of the most direct and effective ways to reduce the width of a confidence interval is to increase the sample size. As the number of observations in a sample grows, the sample mean becomes a more accurate representation of the population mean. This, in turn, reduces the standard error of the mean, which directly influences the interval's width.

The relationship between sample size and interval width is inversely proportional. Doubling the sample size does not necessarily halve the width, but it does lead to a significant reduction. Researchers often conduct power analyses to determine the optimal sample size needed to achieve a desired level of precision.

According to a study published in the Journal of Statistical Planning and Inference, increasing the sample size is often the most effective strategy, especially when dealing with populations that exhibit high variability. A larger sample provides a more stable and reliable estimate of the population parameter, reducing the margin of error.

The Role of Variability

The variability within the population being studied is another critical factor determining confidence interval width. Higher variability, measured by the standard deviation, leads to wider intervals. When data points are more spread out, it becomes more difficult to pinpoint the true population parameter with accuracy.

Reducing variability at the source can be challenging, but sometimes it's possible through careful study design and data collection methods. Stratified sampling, for example, can help reduce variability by dividing the population into subgroups with similar characteristics before sampling.

Moreover, using more precise measurement tools can also help. If the measurements are prone to error, this will naturally increase the variability in the data. Ensuring accurate and consistent data collection practices is crucial for minimizing variability and narrowing confidence intervals.

The Confidence Level Trade-Off

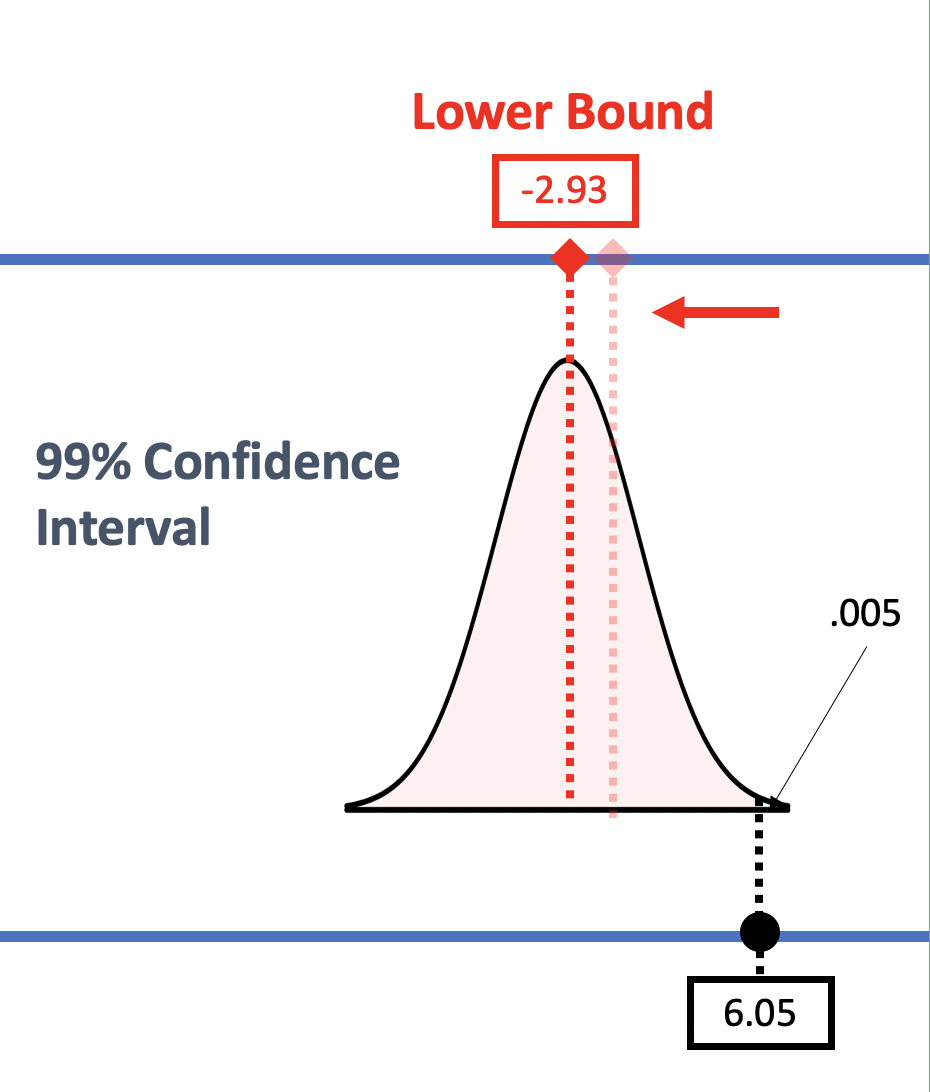
The desired confidence level also influences interval width. A higher confidence level, such as 99%, requires a wider interval to ensure that the true population parameter is captured with greater certainty. Conversely, a lower confidence level, like 90%, allows for a narrower interval but increases the risk of missing the true value.

Choosing the appropriate confidence level involves a trade-off between precision and certainty. While a 99% confidence level may seem desirable, it comes at the cost of a wider interval, which may not be informative. A 95% confidence level is commonly used as a balance between these two factors.

The selection of the confidence level depends heavily on the context of the study and the consequences of making an incorrect inference. In medical research, where the stakes are high, a higher confidence level may be warranted. In other fields, a lower level may be acceptable if the consequences of error are less severe.

Statistical Techniques and Interval Width

The specific statistical technique used to calculate the confidence interval can also influence its width. For instance, using a t-distribution instead of a z-distribution is appropriate when the sample size is small or the population standard deviation is unknown. However, t-distributions generally result in wider intervals, especially with small sample sizes, due to the increased uncertainty.

Furthermore, employing advanced statistical methods like Bayesian analysis can sometimes lead to narrower confidence intervals by incorporating prior knowledge and beliefs into the estimation process. Bayesian credible intervals, while conceptually different from classical confidence intervals, offer a potentially more precise way to quantify uncertainty.

Conclusion

Narrowing the width of a confidence interval is essential for improving the precision and reliability of statistical inferences. Increasing the sample size, reducing variability, and carefully selecting the confidence level are key strategies for achieving this goal. Understanding the interplay between these factors is critical for researchers and decision-makers across various disciplines.

While increasing sample size and reducing variability are generally desirable, they may not always be feasible or cost-effective. Researchers must carefully consider the trade-offs involved and choose the methods that best suit the specific context of their study.

As data continues to proliferate, the ability to extract meaningful insights from it becomes increasingly important. By understanding the factors that influence confidence interval width, we can strive to make more informed decisions and navigate the complexities of an increasingly data-driven world.